3D Schnecken-/Muschel-Modell nach Cortie/Picado
Ein anderes Modell mit wesentlichen Erweiterungen und mehr Möglichkeiten bei der Generierung von Schnecken und Muscheln beschreiben M.B. Cortie 1993 in [1] und J.Picado 2009 in [2].
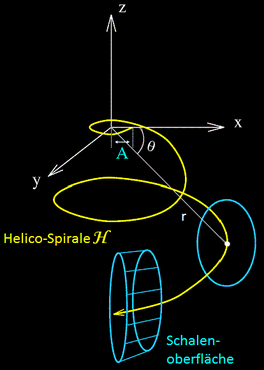
Ausgehend von der Helico-Spirale H (vgl. 3D Modell B. Frassek) und einer Ellipse C
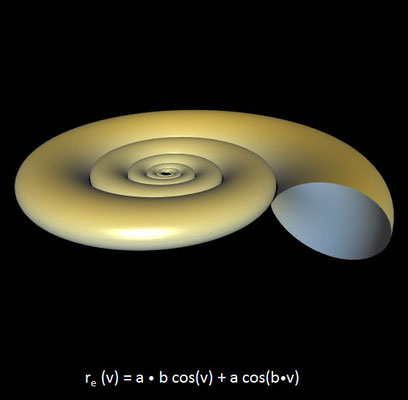
ergibt sich folgendes Grundmodell:
x (u, v) = D [ A sin(β) cos(u) + cos(v) cos(u) re (v) ] e u cot(α)
y (u, v) = [ A sin(β) sin(u) + cos(v) sin(u) re (v) ] e u cot(α)
z (u, v) = [ –A cos(β) + sin(v) re(v) ] e u cot(α)
mit der eliipsenbildenen Funktion
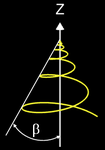
Die folgende Grafik zeigt den Einfluss von α und β auf die Form (Wendelung) von H :
Der Parameter D gibt die Drehrichtung der Wendelung (dextral, sinistral) von H vor (vgl. 3D Modell B. Frassek).
Die mit diesem Grundmodell erzeugbaren Schnecken und Muscheln entsprechen weitesgehend denen, die mit meinem Modell erzeugt werden können.
Allerdings muss die erzeugende Kurve C nicht notwendigerweise eine Ellipse sein. Im folgenden habe ich mit anderen planaren Kurven (Bilder anklicken) und unterschiedlichen Werten für a und b diverse "Phantasiemuscheln" entstehen lassen.
Eine wesentliche Erweiterung des Modells führen Cortie und Picado damit ein, dass die die Schale erzeugende Kurve C mit Hilfe der Winkel μ, θ und Ω beliebig im Raum gedreht werden kann:
Dies führt dann zu folgendem Modell:
x (u, v) = D [A sin(β) cos(u) + cos(v + φ) cos(u + Ω) re (v) – sin(μ) sin(v + φ) sin(u + Ω) re(v)] e u cot(α)
y (u, v) = [A sin(β) sin(u) + cos(v + φ) sin(u + Ω) re (v) – sin(μ) sin(v + φ) cos(u + Ω) re(v)] e u cot(α)
z (u, v) = [–A cos(β) + cos(μ) sin(v + φ) re(v)] e u cot(α)
Dieses Modell erweitern die Authoren noch um die Möglicheit, Rillen, Knoten oder Dornen auf der Schalen-oberfläche erzeugen zu können. Für deren Aufbau genügen einige wenige zusätzliche Parameter:
Hierbei sind
L : Höhe des Knotens bei u = 0
N : Anzahl der Knoten pro Umlauf (Drehung von u um jeweils 2 π)
w1 : Weite (Winkel in °) entlang der Ellipse C
w2 : Weite (Winkel in °) entlang der Helico-Spirale H
P : Position (Winkel in °) des Knotens auf der Ellipse
Zur Überlagerung der Ellipse mit den Knoten wird die Funktion re (u) ersetzt durch die Addition von re (u) mit der knötchenbildenden Funktion rn (u,v).
Für w1 = 0 oder w2 = 0 oder N = 0 ist rn (u,v) = 0; ansonsten ist
Somit besteht das fertige Modell aus insgesamt 16 Parametern:
| Form | Ellipse | Ellipsendrehung | Knoten | Wendelungen | |||||||||||
| D | α | β | A | a | b | φ | μ | Ω | L | N | w1 | w2 | P | umin | umax |
Für die Erzeugung einfacher Texturen oder Farbverläufe gelten die unter Modell B.Frassek aufgeführten Beschreibungen.
Zum eigenen Experimentieren mit Graphing Calculator 3D können Sie unten im Download-Bereich eine .gc3-Datei mit dem Modell von Cortie/Picado herunterladen.
Parameter für Schnecken-/Muschel-Modell Cortie/Picado
In der folgenden Tabelle sind für die Schnecken und Muscheln in der Galerie, die ich mit dem Modell von Cortie / Picado erzeugt habe, die Parameter für deren Grundform angegeben. Die Texturen und Einfärbungen wurden experimentell ermittelt (vgl. "Texturen" unter Eigenes Modell).
| Typ | D | α | β | A | a | b | φ | μ | Ω | L | N | w1 | w2 | P | umin | umax |
| Conus amadis | 1 | 87 | 7 | 7 | 4.3 | 1 | 78 | 0 | 0 | 0 | -29 | 10 | ||||
| Planorbis | 1 | 84 | 85 | 50 | 25 | 45 | 20 | 1 | 5 | 0 | -16 | 11 | ||||
| Epitonium scalare 1 | 1 | 86 | 10 | 90 | 20 | 20 | 45 | 5 | 1 | 3 | 40 | 180 | 0.4 | 40 | -40 | 2π |
| Maurea tigris | 1 | 84.9 | 7 | 47 | 30 | 19 | -36 | 1 | -2 | 1.5 | 16 | 10 | 10 | 30 | -40 | 16 |
| Tectus conus | 1 | 87 | 20 | 76.3 | 20 | 10 | -45 | 5 | 1 | 2 | 16 |
90 |
10 | 0 | -50 | 20 |
| Cymbiola chrys. | 1 | 86 | 12 | 72 | 40 | 14 | 78 | 10 | -10 | 15 | 6 | 6 | 8 | -7 | -30 | 10 |
| Lyonsia | 1 | 39 | 50 | 9 000 | 6 500 | 17 000 | 0 | 1 | 1 | 0 | -3 | 1 | ||||
| Lyria | 1 | 83.9 | 6 | 50 | 40 | 10 | 78 | 1 | -2 | 15 | 8 | 6 | 27 | -18 | -20 | 7.5 |
| Oxystele variegata | 1 | 84.9 | 20 | 47 | 30 | 19 | -36 | 1 | -2 | 0 | -10 | 12 | ||||
| Turritella turbona | 1 | 88.9 | 4 | 10 | 1 | 1 | 55 | 1 | -2 | 0 | -99 | -1 | ||||
| Ammonit | 1 | 83 | 90 | 2.5 | 1 | 0.9 | 1 | 1 | 1 | 0.5 | 15 | 180 | 20 | 10 | -5 | 11 |
|
Struthiolaria |
1 | 87 | 7 | 5 | 1.8 | 1.6 | 70 | 0 | 60 | 0.3 | 26 | 0.1 | 0.05 | -45 | -50 | 7 |
| Triton (sinistral) | -1 | 86 | 11 | 95 | 20 |
35 |
18 | 0 | -44 | 0 | -30 | 11 | ||||
| Wurmschnecke | 1 | 83 | 8 | 180 | 16 | 16 | -55 | 10 | 2 | 0 | -10 | 15 | ||||
| Argonauta | 1 | 70 | 90 | 2.6 | 2 | 1.5 | 0 | 0 | 0 | 0.7 | 40 | 150 | 10 | 5 | -1 | 5 |
| Sinum cymba | 1 | 83 | 20 | 20 | 12 | 12 | 0 | 20 | 0 | 0 | -16 | 11 | ||||
| Tonna variegata 2 | 1 | 82 | 2 | 46 | 38 | 45 | -60 | 1 | 10 | 0 | 0 | 18 | ||||
| Neptunia tab. 3 | 1 | 86.5 | 4 | 46 | 6 | 6 | 36 | 1 | -2 | 0 | -40 | 17 | ||||
| Concha cavalo | 1 | 84 | -12 | 50 | 40 | 20 | 45 | 1 | 0 | 8 | 8 | 6 | 27 | 0 | -5 | 15 |
| Helcion | 1 | 18 | 90 | 450 | 400 | 310 | 0 | 0 | -40 | 0 | -2 | 0 |
Hinweise:
-
Um die lamellenartigen weißen Rippen zu betonen, wurde die erzeugende Funktion zweimal hintereinander ausgeführt, jedoch mit
L = 7 • umax = 6.4 • einfarbig weiß.
-
v im Bereich 0 bis
π
- v im Bereich 0 bis 2