Piet Hein's Super-Ei

Im Jahr 1959 erhielt der dänische Physiker, Mathematiker, Erfinder und Literat Piet Hein (1905 - 1996) [1] von der Stadtverwaltung Stockholm den Auftrag, den Kreisverkehr auf dem neu zu gestaltenden Platz Sergels Torg (s. Fotos [2], [3] rechts) im Zentrum von Stockholm zu gestalten.Welche Form sollte der Kreisverkehr haben? Ein Quadrat hätte den Vorteil, dass der Kreisverkehr parallel zu den Seiten des Platzes verlaufen würde, während ein Kreis den optimalen Verkehrsfluss bieten würde.

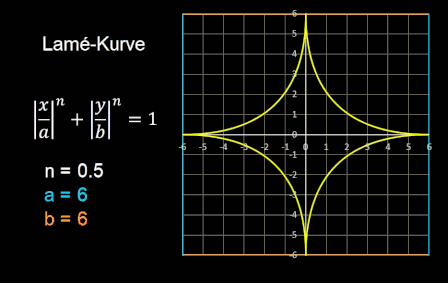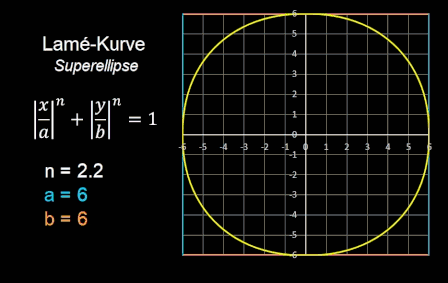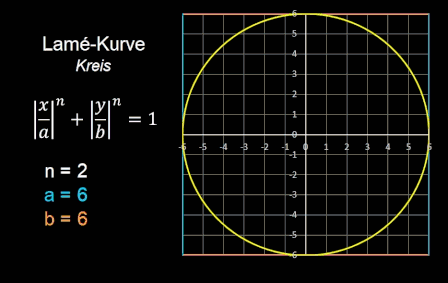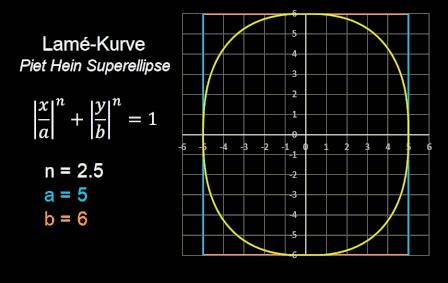
Die Superellipse
Piet Hein experimentierte mit verschiedenen Ellipsen und schlug eine Form vor, die zwischen kreisförmigen und rechteckigen Formen "vermittelt", und nannte sie
Superellipse. Eine Superellipse ist eine geschlossene Kurve und wird durch folgende einfache Gleichung erzeugt (s. auch folgende Animation):
Der Name war zwar neu, doch musste Piet Hein später feststellen, dass sich schon vor ihm jemand mit diesen speziellen Kurven beschäftigt hat...

Für den Sergels Torg verwendete Piet Hein eine Lamé-Kurve mit n = 2.5 und ein Verhältnis a : b = 5 : 6 [9].
Natürlich begnügte sich Piet Hein nicht damit, flache Kurven zu betrachten. Wenn man eine Superellipse um eine ihrer Symmetrieachsen dreht, erhält man ein Super-Ei, wie es z.B. die folgende Abbildung für ein Super-Ei aus poliertem Edelstahl zeigt.
Für die 3D-Darstellung des Super-Eies sollen nun die entsprechenden Formeln in impliziter und in Parameterform hergeleitet werden.
Superellipsoid (Super-Ei) in Parameterdarstellung
Eine Superellipse kann auch in folgender Form dargestellt werden:
Da x und y auch negative Werte annehmen, sind beim Ausrechnen der Terme diese zuerst zu quadrieren und dann mit 1/ε zu potenzieren.
Für diese Superellipse ergibt sich analog zu einem Kreis die folgende Gleichung:
Hierbei - und auch im Folgenden - handelt es sich bei Potenzen mit ε um eine "vorzeichenbehaftete Potenzfunktion" (eng. signed power function), so dass für eine Potenz xp und Vorzeichenfunktion sign gilt:
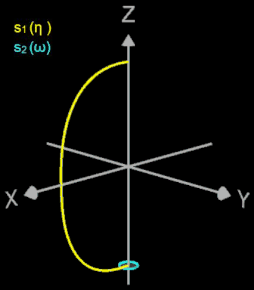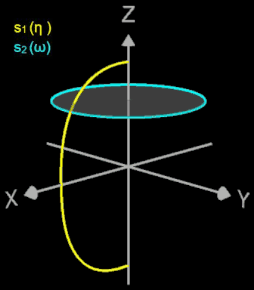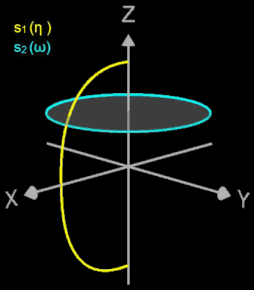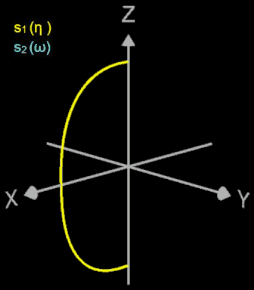
Ein Superellipsoid r lässt sich daher als Sphärisches Produkt (s. auch Erklärung dazu unter 3D Supershape sowie [6]) zweier Superellipsen s1 und s2 erhalten:
Hierbei sind ax , ay , az sind Skalierungsfaktoren entlang der Koordinatenachsen, ε1 und ε2 leiten sich von den Exponenten der beiden Superellipsen ab. ε2 bestimmt dabei die Form eines Querschnittes parallel zur (x | y)-Ebene durch das Superellipsoid, während ε1 die Form eines senkrecht zur (x | y)-Ebene stehenden Querschnittes bestimmt, der durch die z-Achse verläuft.
Für das Super-Ei ergibt sich mit ε1 = 2 / 2.5 = 0.8, ε2 = 1, ax = ay = 3 und az = 4 somit
Super-Ei als Rotationskörper
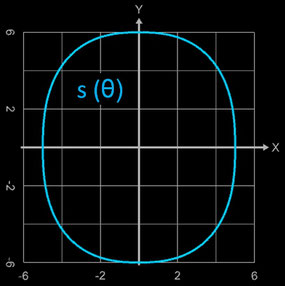
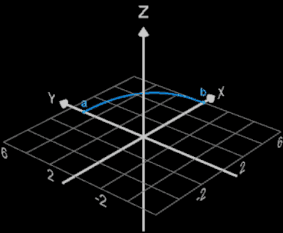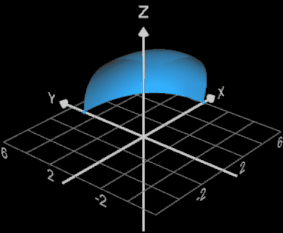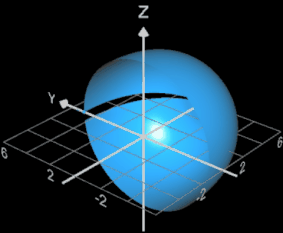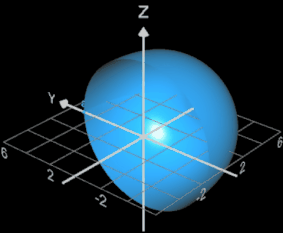
Rotiert man die obige Superellipse s (θ) (s. folgende linke Grafik) um die x-Achse eines Koordinatensystems, so ergibt sich mit a = 5, b = 6 und ε = 2 / 2.5 das Super-Ei als Rotationskörper. Hierbei genügt es, nur die halbe Superellipse, d.h. 0 ≤ θ ≤ π zu rotieren (s. folgende Animation).
Superellipsoid (Super-Ei) in impliziter Darstellung
Die oben hergeleitete Parameterdarstellung des Super-Ellipsoids lässt sich wie folgt umstellen:
Potenzieren der Gleichungen (a) und (b) mit 1 / ε2 und Gleichung (xc) mit 1 / ε1 ergibt:
Addition der Gleichungen (d) und (e) und anschließende Multiplikation mit ε2 / ε1 ergibt:

Addition mit Gleichung (c) ergibt:
und schließlich die allgemeine implizite Darstellung:
.
Für den konkreten Fall des Super-Eies mit
ε1 = 2 / 2.5,
ε2 = 1, ax
= ay = 5 und
az = 6 ergibt sich mit Hilfe des
3D Graphing Calculator das nebenstehende Super-Ei. Schön zu sehen ist das Gitter, das beim Lösen impliziter Gleichungen entsteht im Gegensatz zu den Meridianen des Super-Eies in Parameterform (s. Animation am Seitenanfang).
Die zuvor hergeleitete allgemeine implizite Darstellung für ein Super-Ellipsoid lässt sich für den Fall des Super-Eies, da ε1
= 2 / 2.5,
ε2 = 1 und
ax = ay,
noch etwas vereinfachen:
Standfestigkeit
Eine verblüffende Eigenschaft des Super-Eies ist die Tatsache, dass es stabil aufrecht auf der "Spitze" stehen kann. Kippt man Super-Ei um einen kleinen Winkel in eine beliebige Richtung und lässt es wieder los, so bewegt es sich - ähnlich wie ein "Stehauf-Männchen" - zurück in die Gegenrichtung und schwingt ein paar Male hin und her mit abnehmender Amplitude, bis es sich wieder bis in der stabilen Anfangsposition befindet.
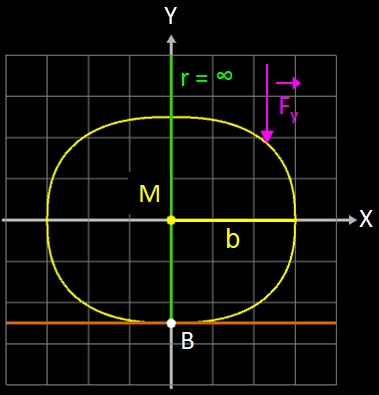
Um dies näher zu betrachten und zu begründen, betrachte man einen senkrechten Schnitt durch die senkrechte MIttelachse (s. gelbe Superellipse in der Animation). Bei einem Super-Ei mit homogener Dichte befindet sich der Massenschwerpunkt M genau im räumlichen MIttelpunkt; er wird in den Ursprung eines x/y-Koordinatensystems gelegt, und das Super-Ei berühre im Punkt B die feste Unterlage (braune Linie).
Die Bedingung für einen stabilen Stand [7] ist, dass der Mittelpunkt C des Krümmumgskreises durch B oberhalb des Massenschwerpunkts M liegt!
Beim aufrecht stehenden Super-Ei ist die "Spitze" ein Flachpunkt, d.h. die Hauptkrümmungen [8] sind in allen Richtungen Null. Der Krümmungskreis hat dort den Radius r = ∞, und sein Mittelpunkt C liegt im Unendlichen (s. dazu auch Intermezzo zum Begriff Krümmung unter Trassierung).
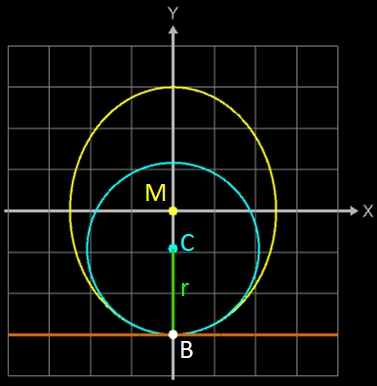
Solange der Mitelpunkt des Krümmungskreises oberhalb des Massenschwerpuntes M des Super-Eies liegt, ist der Stand stabil. Sobald in der Animation gilt Cy ≤ My (s. roter Kreis), kippt das Superei um.
Theoretisch könnte man beliebig viele Super-Eier, deren Flachpunkte in einer zum Untergrund senkrechten Linie übereinander liegen, zu einem Turm stapeln, ohne dass dieser aus dem Gleichgewicht
gerät.
Der stabile Stand in seinen Flachpunkten ist beim Super-Ei unabhängig von der Größe der beiden Halbachsen. Ist die vertikale Halbachse sehr viel größer als die horizontale, so ist der maximale
Kippwinkel, d.h.kurz bevor das Super-Ei umkippt, natürlich deutlich kleiner als zum Beispiel bei einem Verhältnis der Halbachsen von 6:5.
Legt man ein Super-Ei mit seiner Seite auf eine waagerechte Unterlage und lässt keine weitere Kraft auf es einwirken, so scheint es sich in einer
stabilen Position im Punkt B zu befinden. Tatsächlich hat die Krümmung in der x/y-Ebene den Wert Null (s. folgende linke Grafik), der Mittelpunkt des Krümmungskreises liegt im
Unendlichen, also weit über dem Massenschwerpunkt M, woraus Stabilität folgt. Hingegen ist die Krümmung in der y/z-Ebene gleich 1/a, der
Krümmungskreis entspricht dem Schnitt durch B in der y/z-Ebene, der Mittelpunkt C des Krümmungskreises ist identisch mit dem
Massenschwerpunkt M (s. folgende rechte Grafik), woraus Labilität [8] folgt.
Zwar würde theoretisch ein kleiner Kraftstoß
Fy in der x/y-Ebene auf das Ende des Super-Eies (s. folgende linke Grafik) dieses absenken und auspendeln lassen, bis
es sich wieder exakt in der Ausgangsposition befindet. Auch würde theoretisch ein kleiner Kraftstoß Fz
in der y/z-Ebene in Richtung z-Achse (s. folgende rechte Grafik) das Super-Ei exakt entlang
der z-Achse rollen lassen. Praktisch aber sind bei Einwirkung eines Kraftvektors auf das Super-Ei sogar alle 3 Raumkomponenten beteiligt: das Super-Ei torkelt daher mehr oder weniger hin und her,
bis es schließlich zur Ruhe kommt.
Im Gegensatz zum Super-Ei ist bei einem rotationssymmetrischen Ellipsoid (s. folgende Grafik) ein Stand auf der Spitze nicht möglich: der Mittelpunkt C des Krümmungskreises liegt hier unterhalb des Massenschwerpunktes M, beim Versuch, es auf seine Spitze zu stellen, kippt das Ellipsoid sofort um.
Ich konnte nicht widerstehen und habe mir ein Super-Ei gekauft. Das 10 cm hohe Super-Ei besteht aus zwei polierten Edelstahl-Halbschalen und erinnert an die gelbe Plastikkapsel in einem Kinder-Überraschungsei.
Im Film rechts steht es wackelnd auf dem Touch Pad meines Notebooks, während auf dessen Bildschirm im Hintergrund die Animation eines wackelnden Super-Eies (die gleiche wie oben am Seitenanfang) läuft.
Zwei interessante Maße sind die Fläche AS einer Superellipse und das Volumen VS eines Superellipsoids, insbesondere das eines Super-Eies.
Fläche Superellipse
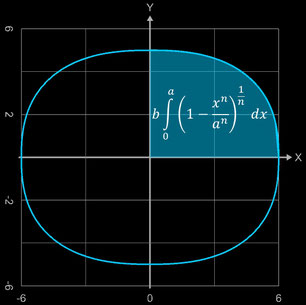
Zur Herleitung der Fläche AS einer Superellipse wird nur die Fläche im 1. Quadranten berechnet; das Ergebnis wird mit 4 multipliziert:
Dieses Integral lässt sich nicht durch elementare Funktionen ausdrücken. Die weitere Herleitung und Lösung [9], [10] ergibt :
Speziell für die Superellipse mit n = 2.5 ergibt sich:
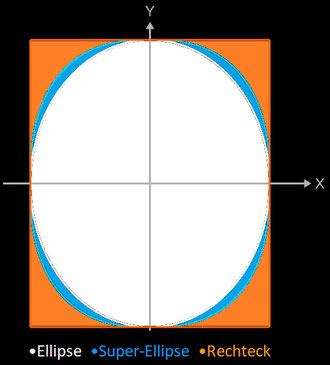
Der Vergleich mit einer einbeschriebenen Ellipse und einem umschriebenen Rechteck ergibt:
AEllipse = π a b ≤ ASuper-Ei ≤ ARechteck = 4 a b
Das oben angegebene Integral lässt sich natürlich auch numerisch lösen:
Mit Hilfe des Graphing Calculator 3D ergibt sich mit der Summierten Simpson-Regel (s. Numerische Integration) für eine Superellipse mit a = 6, b= 5, n =2.5 für die Fläche ein Wert von 101.4280121144567 gegenüber der echten Fläche von 101.428060876121 (Berechnung der Gammafunktionswerte erfolgte mit EXCEL). Dies entspricht einem Fehler von ca. 0.000048 %.

Volumen Super-Ei
Zur Herleitung des Volumens VS eines Superellipsoids wird dieses als Rotationskörper mit Rotation um die x-Achse betrachtet wird. Hierzu wird die Funktion
im 1. Quadranten um die x-Achse rotiert: es entsteht das halbe Superellipsoid; für das Volumen ist das Ergebnis noch mit 2 zu multiplizieren:
Auch dieses Integral lässt sich nicht durch elementare Funktionen ausdrücken. Die weitere Herleitung und Lösung [9], [10] ergibt:
Speziell für das Super-Ei mit n = 2.5 ergibt sich:
Der Vergleich mit einem einbeschriebenen Ellipsoid und einem umbeschriebenen Zylinder ergibt:
AEllipsoid = 4/3 π a b² ≤ ASuper-Ei ≤ AZyl. = 2 π a b²

Das oben angegebene Integral lässt sich natürlich auch numerisch lösen (vgl. mit oben). Mit Hilfe des Graphing Calculator 3D liefert die Summierte Simpson-Regel (s. Numerische Integration) für ein Super-Ei mit a = 6, b= 5, n =2.5 für das Volumen einen Wert von 706.8850663772146, was einem Fehler von ca. 0.00000192 % gegenüber dem tatsächlichen Volumen von ca. 706.885079938187 entspricht.
Nach der Erfindung von Piet Hein tauchten an vielen Stellen Superellipsen auf, sei es in der Architektur oder im Bereich Design (s. Superellipse mania! bei [9]). Noch heute gibt es den Piet-Hein-Shop [11], wo u.a. verschiedene Objekte auf der Basis von Supperellipsen/-ellipsoiden, wie z.B. Lampen, Möbel, Gefäße, Schalen, Super-Eier, etc. zum Verkauf angeboten werden.
Ein großes Super-Ei befindet sich auf dem Gelände von Schloss Egeskov [12] auf der dänischen Insel Fünen:
Das größte Super-Ei der Welt wurde 1999, drei Jahre nach Piet Heins Tod, in der dänischen Kleinstadt Skjern an der Nordseeküste aufgestellt [13]. Dort hatte Piet Hein zu Lebzeiten ein Architekturbüro. Es ist vier Meter hoch und besteht aus Glasfaser mit einem Silber-Bronze-Überzug.
Quellenverweise
[1] https://de.wikipedia.org/wiki/Piet_Hein_(Wissenschaftler)
[2] https://www.skanska.se/vart-erbjudande/vara-projekt/218434/Sergels-Torg%2C-Stockholm
[3] https://commons.wikimedia.org/wiki/File:Sthlm_sergelstorg_MH5Y4176.jpg
[4] https://en.wikipedia.org/wiki/Gabriel_Lam%C3%A9
[5] https://en.wikipedia.org/wiki/Superellipse
[6] Superquadrics and Angle-Preserving Transformations (PDF)
[7] https://de.wikipedia.org/wiki/Standfestigkeit
[8] https://de.wikipedia.org/wiki/Hauptkr%C3%BCmmung
[9] https://www.matematiksider.dk/piethein.html
[10] https://de.wikipedia.org/wiki/Gammafunktion
[12] http://www.astoft.co.uk/herrefyn.htm
[13] https://www.visitvesterhavet.de/nordsee/unsere-staedte/piet-hein