Weitere Verfahren zur Nullstellenbestimmung

Auf dieser Seite werden weitere Verfahren zur Nullstellenbestimmung, d.h. zum Bestimmen der Lösung(en) der Gleichung f (x) = 0, kurz vorgestellt:

Die Verfahren sind Weiterentwicklungen des Sekanten-, Newton- oder Halley-Verfahrens mit dem Ziel, die Konvergenzordnung und Effizienz (s. Iterative Verfahren zur Nullstellenbestimmung) zu erhöhen und/oder die Ableitung (oder zumindest höhere Ableitungen) nicht berechnen zu müssen, indem diese durch entsprechende Approximationen ersetzt werden.

Während bei den "Klassikern", z.B. beim Newton-Verfahren, in jedem Iterationsschritt eine einzige Verfeinerung bei der Näherung an die Nullstelle erfolgt, sind die meisten neueren Verfahren zwei- oder mehrstufige Verfahren. Dies bedeutet z.B. bei einem zweistufigen Verfahren, dass zunächst in einem Zwischenschritt ("Vorhersage", engl. predictor step) eine erste Näherung berechnet wird (oftmals mit dem Newton-Verfahren) und diese dann am Ende jedes Iterationsschrittes verbessert wird (engl. corrector step). In den letzten beiden Dekaden ist diese Zwei- oder Mehrstufigkeit kennzeichnend bei der Entwicklung weiterer Verfahren.

_______________

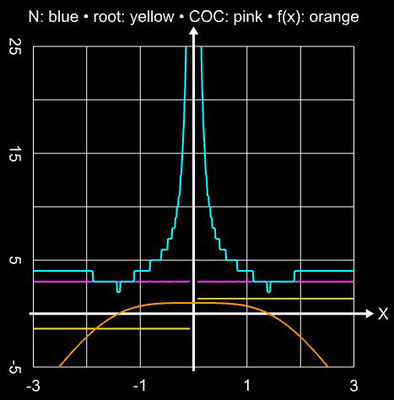
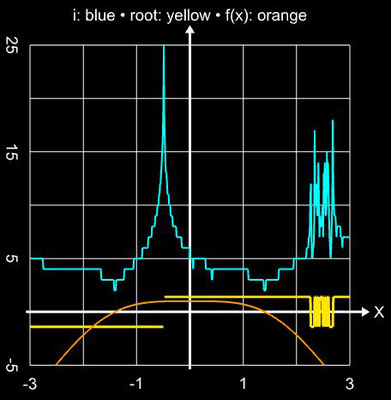
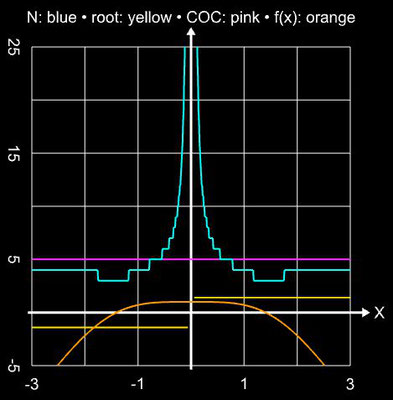
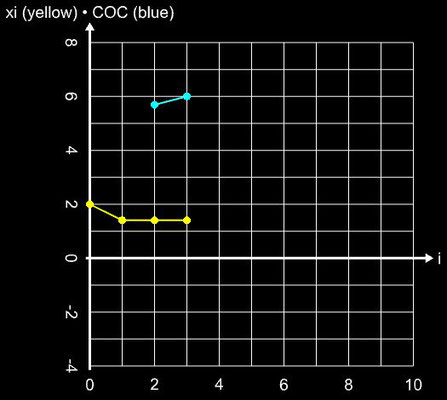
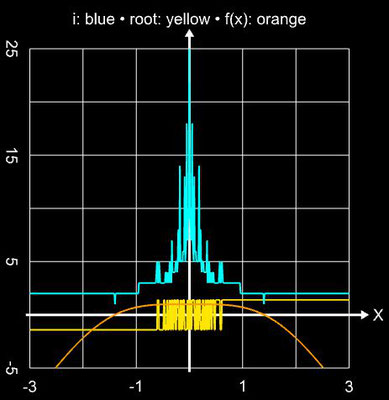
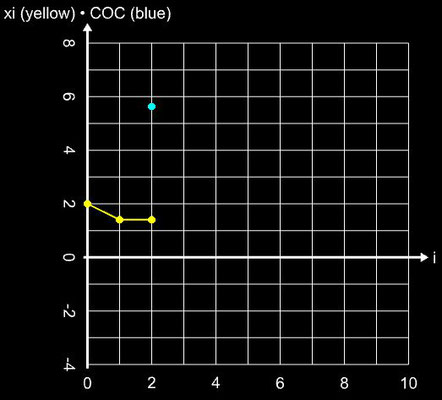
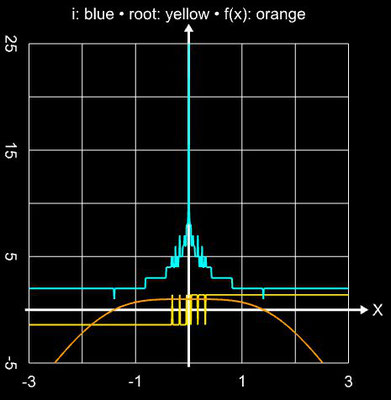
Als übergreifendes Anwendungsbeispiel für die im Folgenden betrachteten Verfahren diene die Funktion
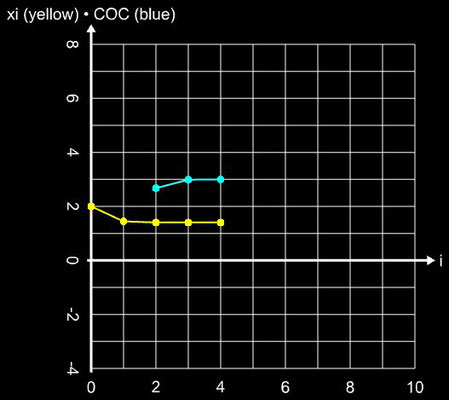
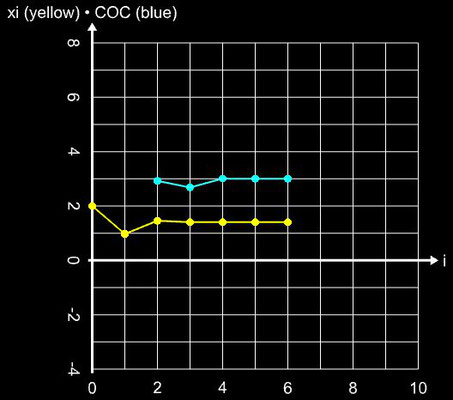
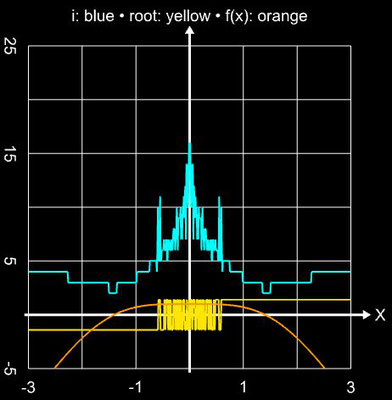
f (x) = sin ² (x) - x² + 1 mit ihren beiden Nullstellen ξ _0,1 ≈ ±1.404491648215341226... Für die schrittweise Darstellung der Iteration wurde x₀ = 2 gesetzt, für den Einzugsbereich wurde das Intervall [-3, 3] (Schrittweite 100) verwendet. Für beide Darstellunegn wurde die maximale Anzahl an Iterationen i_max auf 25 begrenzt und als Abbruchkriterium | x_i – x_i-1 | ≤ 10^-15 gewählt.

Beweise für die Konvergenzordnung sowie Berechnungen für weitere Funktionen finden Sie in der jeweiligen Publikation, weitere Funktionsbeispiele (demnächst) auch unter Verfahrensvergleich.

________________

Zwei Dateien (Step und Range) für eigene Berechnungen mit dem Graphing Calculator 3D finden Sie unten im Download-Bereich.

Ersetzt man in der Iterationsvorschrift des Newton-Verfahrens

die Ableitung f ' der Funktion f durch den (rechtsseitigen) Differenzenquotienten (s. Differential) d (x_i) mit

so erhält man mit h = f (x_i) die Iterationsvorschrift für das Steffensen-Verfahren:

Dieses wurde laut [1] zuerst durch Steffensen vorgenommen ("To circumvent on the derivative calculation in Newton’s iteration, Steffensen first coined the following second order convergent scheme ...").

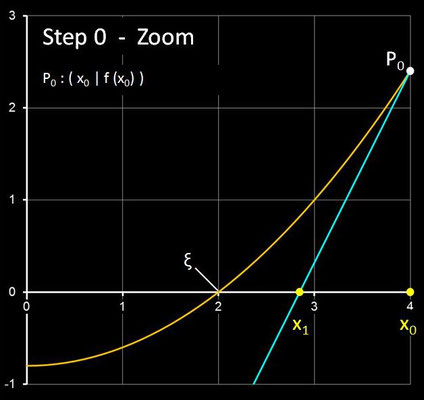
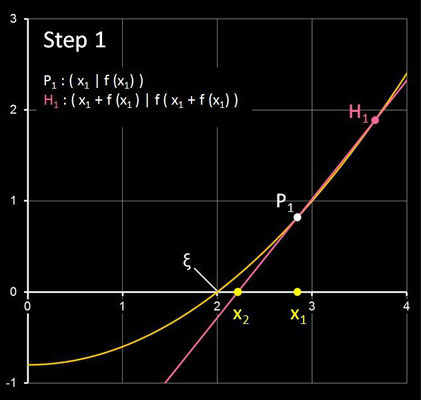
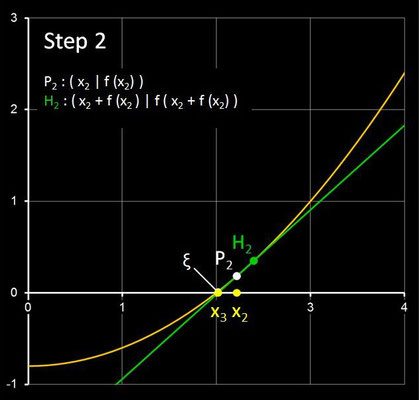
Für einen Punkt P_i ( x_i | f(x_i) ) im i-ten Schritt ist d (x_i) die Steigung der Geraden durch P_i und den Hilfspunkt
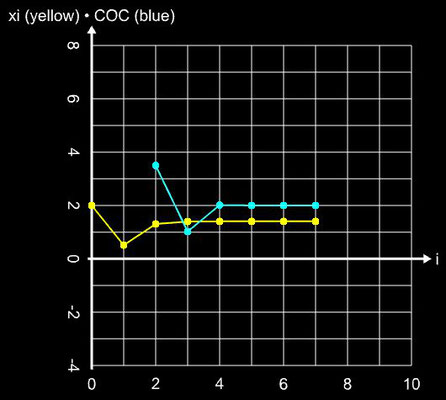
H_i ( x_i +f(x_i) | f (x_i +f(x_i)) ). Die folgende Galerie zeigt die ersten drei Schritte des Steffensen-Verfahren anhand der Funktion f (x) = 0.2 x² - 0.8 mit der Nullstelle ξ = 2 und dem Startwert x₀ = 4.        

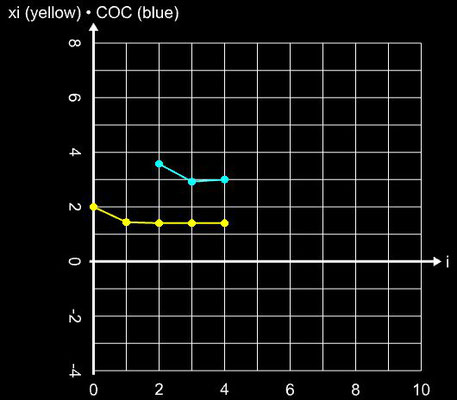
Die Konvergenzordnung und Effizienz des Verfahrens entsprechen denen des Newton-Verfahrens, d.h.
q = 2 und CE = 1.414. Angewandt auf die obigenBeispielfunktion ergibt sich folgendes Ergebnis:

Auf Grund der "engen Verwandschaft" mit dem Newton-Verfahren ist zu erwarten, dass bezüglich des Konvergenzverhaltens auch beim Steffensen-Verfahren die gleichen Problemfälle wie beim Newton-Verfahren auftreten. In der Tat treten solche Fälle wie Divergenz oder Sprünge (z.B. bei f (x) = sin (x)) auf. Bisher ist es mir jedoch nicht gelungen, Funktionen mit entsprechenden Startwerten zu finden, bei denen Oszillationen (s. bei B. Oszillationen unter Newton-Verfahren) auftritt.

Der Verfasser stellt ein Sekanten-ähnliches Verfahren vor, das wie das Tiruneh-Verfahren superquadratisch, d.h. mit  q = 2.414, konvergiert [2] und mit dem Startwert x₀ folgende Iterationsvorschrift besitzt:

In [2] wird zwar die Konvergenz bewiesen, die Herleitung dieser Iterationsvorschrift wird jedoch nicht gezeigt. Die Effizienz des Verfahrens beträgt CE = 1.554. Hier die Ergebnisse bei Anwendung auf die Beispielfunktion:

Ausgehend von der Umkehrfunktion zu f und einer Taylor-Reihenentwicklung leitet Chebyshev für i = 0, 1, 2, ... das folgende Verfahren her:

Es besitzt die Konvergenzordnung q = 3 und die Effizienz CE = 1.442.

Jisheng Kou und Yitian Li entwickelten eine Variante des Chebyshev-Verfahrens, das ohne die zweite Ableitung auskommt und die Konvergenzordnung q = 4 und Effizienz CE = 1.587 aufweist [3].

Kasturiarachi kombiniert in [4] das Sekantenverfahren mit dem Newton-Verfahren, wobei letzteres einen Zwischenschritt darstellt:

Das Verfahren besitzt die Konvergenzordnung q = 3. Im Vergleich zum Newton-Verfahren ist pro Iterationsschritt ein weiterer Funktionswert zu berechnen, woraus sich eine Effizienz von CE = 1.442 ergibt.

Ausgehend vom Steffensen-Verfahren erweitert P. Jain in [5] dieses mit folgendem Ergebnis:

und erhält somit ein ableitungsfreies Verfahren mit der Konvergenzordnung q = 3 und einer Effizienz von
CE = 1.442.

Der Autor entwickelt in [6] ein zweistufiges Verfahren, bei dem als Predictor das von Noor & Noor in [7] vorgestellte Verfahren dient, das selbst wiederum eine zweistufige Modifikation des Halley-Verfahrens ist.
Für i = 0, 1, 2, ... lautet die Iterationsvorschrift:

Das Verfahren hat eine kubische Konvergenzordnung (q = 3) mit einer Effizienz CE = 1.442.

Ausgehend von dem unbestimmten Integral, das sich aus dem Newton-Verfahren ergibt

verwenden die Verfasser bei der Herleitung ihres Verfahrens [8]  für die näherungsweise Berechnung des Integrals (Quadratur) kein Rechteck, sondern ein Trapez und erhalten schließlich für i = 0, 1, 2, ... die folgende Iterationsvorschrift:

mit einer Konvergenzordnung von q = 3 und der Effizienz CE = 1.442. Angewandt auf die Beispielfunktion ergibt sich das folgende Ergebnis:

In [9] entwickeln Kou et al. modifizierte dreistufige Newton-Verfahren, die ohne die zweite Ableitung auskommen und allesamt die Konvergenzordnung q = 5 besitzen, wie z.B. das folgende ("FAN"), dessen Zwischenschritt U_i+1 auf dem Verfahren von Weerakoon/Fernando [8] beruht und für i = 0, 1, 2, ... lautet:

Die Effizienz beträgt CE = 1.495.

Mittels einer Taylor-Reihenentwicklung der Funktion und Einsetzen der Iterationsvorschrift des
Halley-Verfahrens leiten die Verfasser ein neues zweistufiges Verfahren MH1 (Modified Halley Method) her [10] mit folgender Iterationsvorschrift

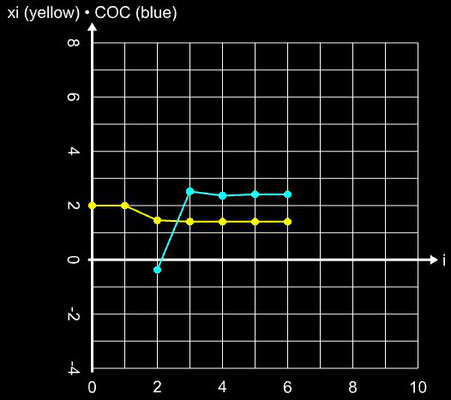
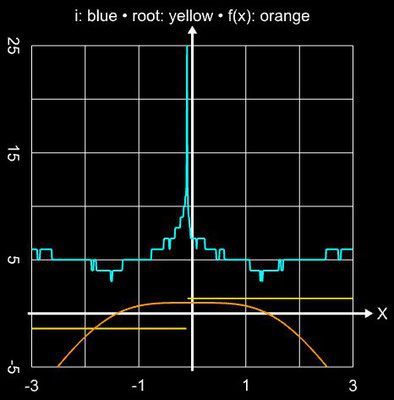
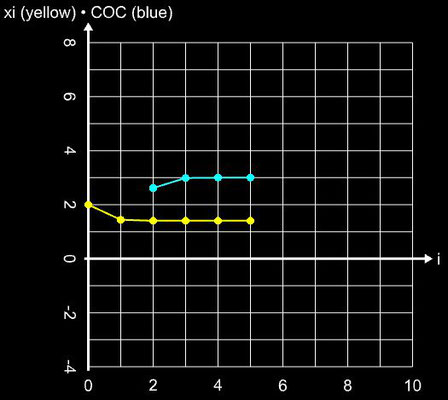
Hierbei dient das Newton-Verfahren (Gleichung 1) als Predictor und die zweite Gleichung als Corrector. Die Konvergenzordnung beträgt q = 6 bei einer Effizienz von 1.431. Die folgende Galerie zeigt die Anwendung des Verfahrens auf die Beispielfunktion (s.o.).

Um die Effizienz des Verfahrens MH1 zu verbessern, wird die zweite Ableitung, basierend auf bereits berechneten Vorgängerwerten der Iteration, durch eine kubische Approximation ersetzt:

und es ergibt sich die Iterationsvorschrift für MH2:

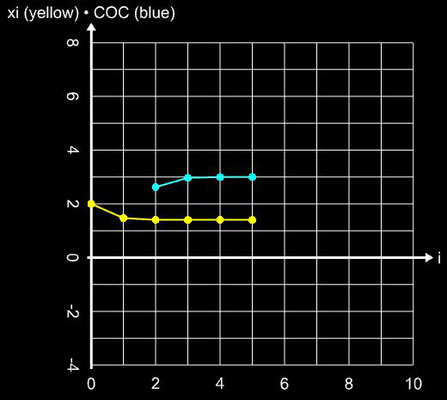
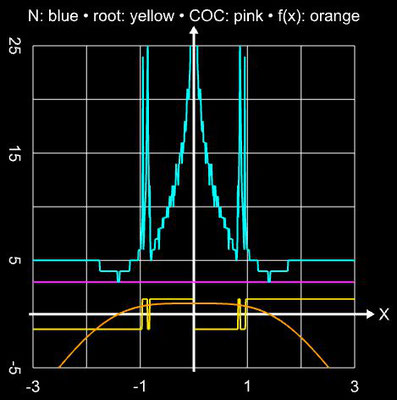
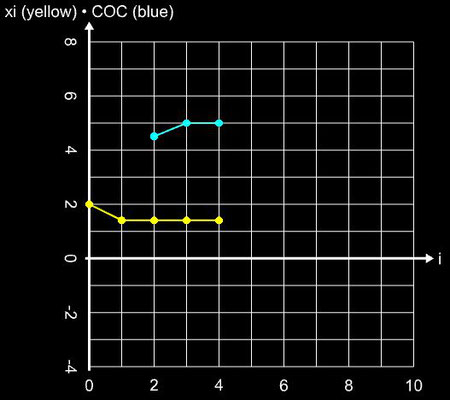
Da nunmehr nur zwei Funktionswerte und zwei Ableitungen zu berechnen sind, beträgt die Effizienz bei gleicher Konvergenzordnung von q = 6 nun CE = 1.565.  Angewandt auf die Beispielfunktion ergibt sich:

Quellenverweise

[1]    M. Kumar, A. Kumar Singh, A. Srivastava, Various Newton-type iterative methods for solving
        nonlinear equations, Journal of the Egyptian Mathematical Society (2013) 21, 334–339

[2]    R. Thukral, A New Secant-type Method for Solving Nonlinear Equations,
        American Journal of Computational and Applied Mathematics 2018, 8(2): 32-36

[3]   Jisheng Kou, Yitian Li, On Chebyshev-type methods free from second derivative,
       Commun. Numer. Meth. Engng 2008; 24:1219–1225

[4]    Kasturiarachi, A. B. (2002), Leap frogging Newton’s method,
        Int. J. Math. Educ. Sci. Technol. 33: 521–527

[5]    Jain, P. (2007), Steffensen type methods for solving non-linear equations,
        Appl. Maths. Comp. 194: 527–533

[6]    M. S. M. Bahgat, New Two-Step Iteration Methods for Solving Nonlinear Equations,
       Journal of Mathematics Research; Vol. 4, No. 3 (2012), S.128 ff

[7]    Noor, M. A., Inayat Noor, K. (2007), Predictor-corrector Halley method for nonlinear equations,
       Journal of applied mathematical and computation, 188, 1587-1591

[8]    S. Weerakoon, T. G. I. Fernando,
        A Variant of Newton’s Method with Accelerated Third-Order Convergence,
        Applied Mathematics Letters 13 (2000) 87-93

[9]    Kou JS, Li YT, Wang Xi, Some modifications of Newton’s method with fifth-order convergence,
        Journal of Computational and Applied Mathematics 209 (2007) 146 – 152

[10]  O. Solaiman, I. Hashim (2018), Two new efficient sixth order iterative methods for solving
        nonlinear equations, Journal of King Saud University – Science

Download

Hinweis:    Insbesondere für ableitungsfreie Verfahren und die COC-Berechnungen sollte beim Graphing Calculator 3D nicht die Standardbibliothek sondern die  Bibliothek APFLOAT mit einer hinreichend großen Anzahl an Nachkommastellen (z.B. 200 Digits) eingestellt werden, da die berechneten Werte bei den Iterationsschritten sehr klein sein können und das Verfahren vorzeitig oder mit einem "Division durch Null"-Fehler abbrechen kann (s. dazu auch die Ausführungen ganz unten beim Sekanten-Verfahren).