3D Birne
Im Gegensatz zum 3D Apfel, 3D Paprika und 3D Kürbis handelt es sich bei der 3D Birne (nach einer Idee von Valentina Galati [1]) um eine implizite Fläche mit der erzeugenden Funktion
(((x²+y²+0.2*z²)²-(x²+y²)) ((x-0.55-0.05*(1.1z+1.75))²+y²+(1.1z+1.75)²-2.3)-0.5) •
(((x-0.3(z-1.5) -0.1)²+y²+0.1(z-1.5)6 -0.006) ((x-0.4)²+y²+(z-2)²-0.03)-0.001) = 0
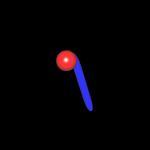
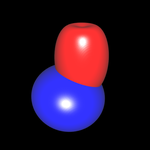
Die Birne besteht aus mehreren Komponenten (impliziten Funktionen), aus denen durch Verschmelzen Stiel und Körper entstehen. Diese Technik ist unter Implizite Flächen (Operationen auf Impliziten Flächen) beschrieben. In der folgenden Galerie wird die Modellierung der Birne aus den Einzelkomponenten dargestellt.
Multipliziert man (vgl. Implizite Flächen) die Komponenten des Stiels (s. Tabelle unten) mit denen des Körpers (s. Tabelle unten), so ergibt sich die obige Gleichung und die fertige Birne:
Für eine halbwegs realistische Darstellung kann man darauf natürlich verzichten und Teilkomponenten entsprechend einfärben.
| Objekt | Funktion | Teilobjekt |
|
3D Birne
|
((x-0.3*(z-1.5) -0.1)^2+y^2+0.1*(z-1.5)^6-0.006)*((x-0.4)^2+y^2+(z-2)^2-0.03)-0.001 = 0
((x^2+y^2+0.2*z^2)^2-(x^2+y^2))*((x-0.55-0.05*(1.1*z+1.75))^2+y^2+(1.1*z+1.75)^2-2.3)-0.5 = 0 |
Stiel
Körper
|