Pseudo-Zufallszahlen

Was der Troll sagt, ist richtig:
Es ist unmöglich, definitiv zu beweisen, ob eine gegebene Zahlenfolge und der Generator, der sie erzeugt hat, zufällig sind. So kann der Troll seit vielen Jahren perfekte Zufallszahlen generiert haben, als Dilbert gerade in dem Moment hereinspaziert, als er zufällig sechs Neunen hintereinander nennt.
Für einige Themen / Berechnungen, wie z.B. bei der Simulation eines Galton-Bretts oder bei den Spherical Harmonics, wird eine Sequenz von Zufallszahlen benötigt; diese Sequenz soll einerseite "zufällig", andererseits jedoch reproduzierbar sein!
Beim 3D Galton-Brett ist die Reproduzierbarkeit auf Grund der Animation zwingend erforderlich, bei den Spherical Harmonics oder anderen Flächen / Objekten mit zufällig gewählten Parametern wird somit sicher gestellt, dass zwar zufällige Flächen / Objekte entstehen, diese aber bei Interesse/Gefallen reproduziert und editiert werden können.
Zwar bietet der Graphing Calculator 3D die Funktion rand zum Erzeugen von Zufallszahlen im Intervall [0, 1] (ähnlich auch bei anderen Programmen und EXCEL), jedoch werden mit jedem Durchlauf einer Animation oder beim Klicken auf ein Bedienelement neue Zufallszahlen berechnet, wodurch ein gewünschtes und zu editierendes Objekt adhoc durch ein neues ersetzt wird :-((
Daher muss für die genannten Anwendungen ein Algorithmus (Zufallszahlen-Generator, engl. Random Number Generator, kurz: RNG) programmiert werden, der Zufallszahlen erzeugt. Dies ist ein Widerspruch in sich, da ein Algorithmus determiniert ist und somit jeder Nachfolger einer erzeugten Zufallszahl bereits zwingend feststeht. Es lassen sich daher nur "Pseudozufallszahlen" erzeugen (wie dies auch die Funktion rand macht), die aber dem echten Zufall recht nahe kommen sollen; folglich soll der Zufall deterministisch möglichst gut nachgestellt werden.
Intuitiv folgert man aus dem Begriff "Zufallszahl", dass kein Muster, keine Struktur in der Folge der erzeugten Zahlen erkennbar sein soll. Allgemeine Forderungen an einen Zufallszahlen-Generator (engl. Random Number Generator, RNG) sind:
-
Gleichverteilung
Die Zufallsfolge genügt der Gleichverteilung über einem bestimmten Zahlenbereich.
-
Unvorhersagbarkeit
Der Nachfolger einer Zahl darf nicht vorhersagbar sein. Dies bedeutet, dass der Konstruktionsmechanismus komplex genug sein muss, um aus ihm nicht unmittelbar das Konstruktionsprinzip ablesen zu können.
-
Reproduzierbarkeit
Um die Fehlersuche zu erleichtern und verschiedene Simulationen einfacher miteinander vergleichen zu können, ist es wichtig, dass eine einmal erzeugte Zufallsfolge immer wieder reproduziert werden kann (s. obige Anforderungen).

Die Konstruktion / Untersuchung geeigneter Zufallszahlengeneratoren ist ein spezielles Gebiet der Mathematik und umfasst Teilgebiete der Algebra, Zahlentheorie und Stochastik. so dass hier nur einige wenige Aspekte zur Lösung der oben genannten Aufgabe, "reproduzierbare Zufallszahlen" zu erzeugen, betrachtet werden können.
Kongruenzgeneratoren
Ich habe dazu auf Kongruenz-Generatoren [1], [2] zurückgegriffen, die in vielen Laufzeitbibliotheken von Programmiersprachen verwendet werden und zufällig aussehende Zahlenfolgen erzeugen.
Ein Linearer Kongruenzgenerator (kurz: LCG) ist eine rekursive Funktion (vgl. Iteration)
xi+1 = (a xi + b) mod m mit a, b ∊ {1, 2, … , m-1}, Startwert x0 ∊ {0, 1, … , m-1}, m ∊ {2, 3, 4, ...}, i ∊ |N0,
die eine periodische Folge ganzzahliger Pseudozufallszahlen {x0, x1,..., xi} in M = {0, 1, ... , m-1} erzeugt.
Abhängig vom Startwert x0 ("Saat", engl. seed) entsteht jeweils eine andere Folge. Ist b = 0, so nennt man den Generator Multiplikativer Kongruenzgenerator. Falls m genügend groß ist, können die erzeugten Zufallszahlen mit der Vorschrift
in das Intervall [0, 1] transformiert werden, um eine ausreichend feine Unterteilung zu erhalten.
Anmerkung: Der Graphing Calculator 3D verfügt nicht über die Funktion mod, die den Rest einer
ganzzahligen Division liefert; sie kann aber folgendermaßen
realisiert werden:
mod (a, m) = a - floor (a/m) * m.
Die Qualität der Folge der Zufallszahlen hängt hierbei entscheidend von den Parametern a, b und m ab. Erstrebenswert ist zum einen eine Folge mit maximaler Periodenlänge. So liefert z.B. der folgende LCG
xi+1 = (7 xi + 3) mod 800 und x0 = 1
die Folge 1, 10, 73, 514, 401, 410, 473, 114, 1, 10, 73, ... und somit lediglich eine Periodenlänge von 8.
Donald Knuth stellte dazu für den oben definierten LCG die notwendigen Bedingungen auf, für die ein LCG eine maximale Periodenlänge m liefert [3]:
- b und m sind teilerfremd
- p | (a − 1) f¨ur alle Primteiler p von m
- 4 | (a − 1) falls 4 | m.
Die Erfüllung dieser Bedingungen garantiert jedoch noch keinen guten Zufallsgenerator!
So erzeugt z.B. der LCG
xi+1 = (1 xi + 1) mod 800 mit x0 = 1
die Folge 1, 2, ..., 799, 0, 1, 2, ... mit maximaler Periodenlänge, die aber ganz sicher nicht den Anspruch an eine Zufallsfolge erfüllt.
Beispiele für RNGs mit maximaler Periode:
| Autor | Funktion | Periode | |
| RNG 1 | Knuth [4] | xi+1 = (137 xi + 187) mod 216 | 216 |
| RNG 2 | drand48 in C++ | xi+1 = (25214903917 xi + 11) mod 248 | 248 |
| RNG 3 | Park Miller [5] | xi+1 = 75 xi mod (231 - 1) | 231 - 1 |
| RNG 4 | Marsaglia [6] | xi+1 = 75 xi mod (238 - 401) | 238 - 401 |
| RNG 5 | Marsaglia [6] | xi+1 = (534059 xi - 4416 xi-1 ) mod (231 - 69) |
(231 - 69) 2 ≈ 262 |
Um die Qualität eines Zufallszahlengenerators zu untersuchen, wurde eine Vielzahl meist sehr aufwendiger statistischer Tests entwickelt, wie z.B.
- X² und Kolmogorov-Smirnov-Test auf Gleichverteilung
- Gap-Test auf Auto-Korrelation (Überprüfung der Intervalllängen bis zum Wiedererscheinen der gleichen Zahl)
- Poker-Test auf Auto-Korrelation (wie viele unterschiedliche Zahlen enthalten alle Quintupel der Zahlenfolge)
- Spektraltest auf stochastische Unabhängigkeit
- ...
Geometrische Tests auf Muster
Bildet man für die von einem Generator erzeugte Sequenz der Zufallszahlen z0,
z1, z2, … (s.o.) die Paare
(z0, z1), (z1, z2), (z2, z3), … bzw. die Tripel (z0, z1, z2), (z1, z2, z3), (z2, z3, z4), … und bildet diese in die Fläche [0, 1]² bzw. den Einheitswürfel [0, 1]³ ab, würde man erwarten, dass die Punkte in der Fläche bzw. dem Raum gleichverteilt sind, wie es die folgenden beiden Grafiken zeigen.
Hyperebenen
Bei Kongruenzgeneratoren ist dies aber nicht der Fall. Marsaglia zeigte [7], dass für jeden Kongruenzgenerator die erzeugten Punkte im n-dimensionalen Einheitswürfel [0, 1]n (n>2) auf Hyperebenen liegen. Dies kann z.B. bei Simulationen, bei denen mehrere aufeinander folgende Zufallszahlen benötigt werden (s. auch unten bei Normalverteilte Zufallszahlen), zu Problemen führen. Die maximal mögliche Anzahl an Hyperebenen im n-dimensionalen Einheitswürfel [0, 1]n beträgt
jedoch ist die tatsächlich erreichte Anzahl an Hyperebenen meist deutlich kleiner, in ungünstigen Fällen sogar sehr klein.
So ist z.B. für den LCG im TI-59 (ich war Ende der 70er stolzer Besitzer des damals sündhaft teuren programmierbaren Taschenrechners mit Magnetstreifen von Texas Instruments) mit der Vorschrift
xi+1 = (24298 xi + 9991) mod
199017 [8]
die Anzahl der Hyperebenen im 3-dimensionalen Einheitswürfel mit 12 deutlich kleiner als
die maximale Anzahl von 106:
Wünschenswert ist jedoch eine möglichst große Anzahl an Hyperebenen mit möglichst kleinem Abstand d.
L'Ecuyor [9] gibt eine untere Schranke für diesen Abstand an mit
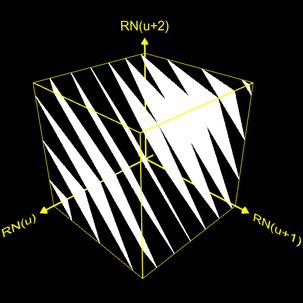
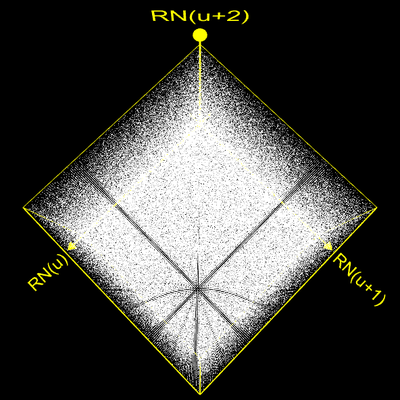
sowie ermittelte Werte für eine Vielzahl von Generatoren. Bei der folgenden linken Grafik mit dem Generator RNG 1 von Knuth (s.o.) erkennt man deutlich die Hyperebenen; bei der rechten Grafik zum RNG 3 von Park Miller liegen die Abstände der Hyperebenen bei ca. 0.00156 [9] und sind, auch wegen der "kleinen" Anzahl von 900 000 Punkten in Relation zur maximalen Periode, nicht mehr als solche zu erkennen.
Noise Sphere Test
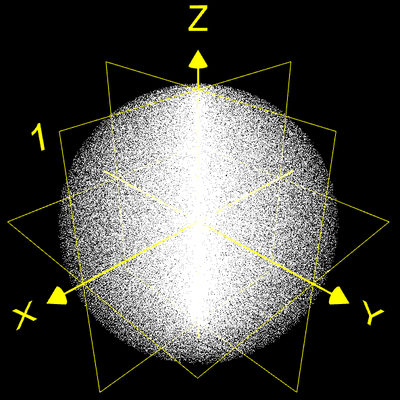
Beim Noise Sphere Test [10] werden die Tripel (zi, zi+1,
zi+2) von Zufallszahlen in Polarkoordinaten abgebildet:
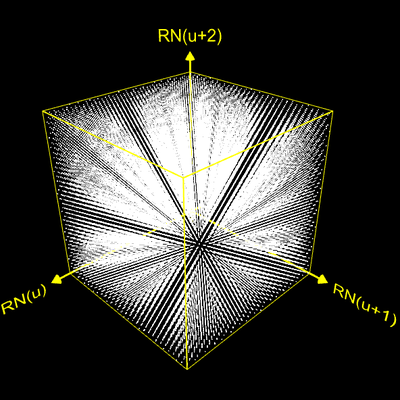
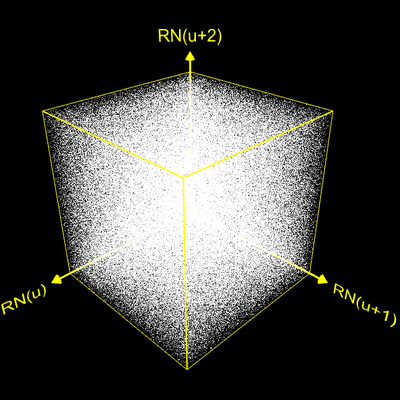
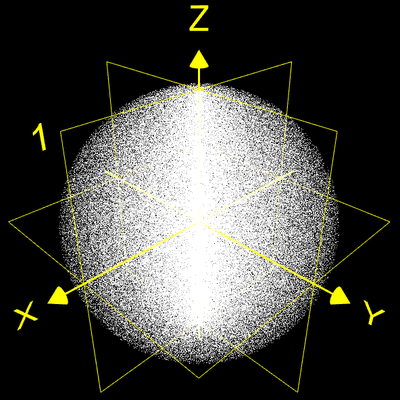
Sind in der Sequenz der generierten Zufallszahlen aufeinander folgende Zahlen stochastisch unabhängig, so ergibt sich eine Gleichverteilung der entsprechenden Punkte in der Einheitskugel ohne erkennbare Strukturen, wie die folgende Abbildung zeigt.
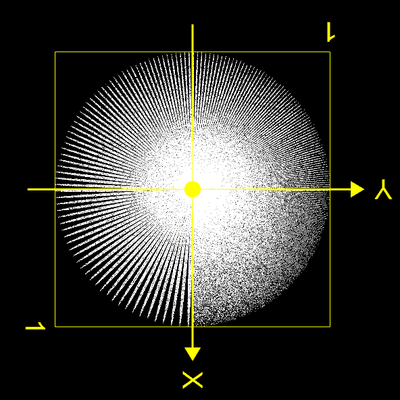
Hingegen erkennt man in den beiden ersten folgenden Grafiken deutliche Strukturen, während beim Park Miller Generator mit seiner großen Anzahl an dicht liegenden Hyperebenen (s.o.) bei 500 000 Punkten keine Strukturen erkennbar sind.
Einen anderen Weg zur Erzeugung von Pseudo-Zufallszahlen beschreitet der Cliff-Generator [11]:
z i+1 = | (100 ln (z i)) mod 1 | mit z0 = 0.1
der Zufallszahlen in [0, 1] erzeugt. In allen folgenden Grafiken sind deutliche Strukturen zu erkennen, wenngleich auch in [11] behauptet wird, dass der Generator den Noise Sphere Test bestehen würde (an einer Klärung des Sachverhalts bin ich dran).
Normalverteilte Pseudo-Zufallszahlen
Für manche Anwendugen werden normalverteilte Zufallszahlen benötigt (s. auch Normalverteilung).
Diese lassen sich zum Beispiel mit der Box-Muller-Methode erzeugen [12]. Hierbei wird eine zweidimensionale Gleichverteilung in eine bivariate Normalverteilung transformiert.
Sind x1 und x2 stochastisch unabhängige, gleichverteilte Zufallszahlen aus [0, 1], dann liegt für z1 und z2 mit
eine Normalverteilung mit µ = 0 und σ² = 1 (Standardnormalverteilung) vor. Mit Hilfe der Vorschrift
kann eine durch µ und σ bestimmte Normalverteilung erzeugt werden.
Die folgende Grafik zeigt die sich ergebende Standardnormalverteilung für 1000 000 gleichverteilter Zufallszahlen. Die cyanfarbenen Kreise haben die Radien σ, 2σ und 3σ.
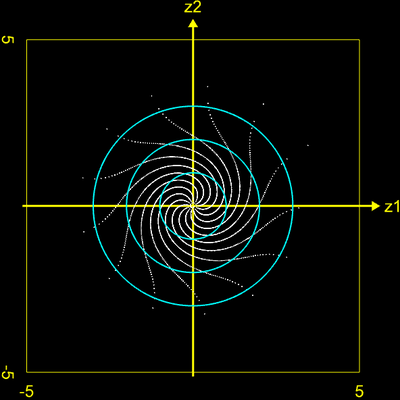
Wird für die Erzeugung der Zufallszahlen ein LCG verwendet, so liegen die Punkte (z1, z2) auf spiralförmigen Kurven, wie dies in den folgenden drei Grafiken für verschiedene Generatoren mit maximaler Periodenlänge, jedoch sehr kleinem m (2048) dargestellt ist.
Die folgenden Grafiken zeigen die entstehenden Strukturen mit den Generatoren TI-59, RNG 1 (Knuth), Cliff und RNG 3 (Park Miller).
|
|
2x auf Grafik klicken für maximales Zoom! |
Abschließend sei noch erwähnt, dass für die am Anfang dieser Seite gestellte Aufgabe "realisiere einen Zufallsgenerator mit reproduzierbarer Sequenz" sich insbesondere Generatoren wie die von Park Miller (RNG 3) und Marsaglia (RNG 4) eignen ...
Quellenverweise
[1] https://de.wikipedia.org/wiki/Kongruenzgenerator
[2] Donald E. Knuth, The Art of Computer Programming, Vol. 2, Addison-Wesley,1997, Seite 9
[3] ebenda, Seite 16
[4] ebenda, Seite 90
[5] Communication of the ACM, July 1988, Vol. 31, No.10 (PDF)
[6] Communication of the ACM, July 1993, Vol. 36, No.7, page 107 (PDF)
[8] Use of the TI 59 with applications to probability and statistical analysis (PDF), Seite 14
[9] Pierre L'Ecuyer, Random Number Generation (PDF)
[10] http://mathworld.wolfram.com/NoiseSphere.html
[11] http://mathworld.wolfram.com/CliffRandomNumberGenerator.html
[12] http://mathworld.wolfram.com/Box-MullerTransformation.html


![Gleichverteilung von Punkten in [0, 1]²](https://image.jimcdn.com/app/cms/image/transf/dimension=1920x400:format=png/path/scee86bccd27a6ab2/image/iad7ac893048af666/version/1539261184/image.png)
![Gleichverteilung von Punkten in [0, 1]³](https://image.jimcdn.com/app/cms/image/transf/dimension=1920x400:format=png/path/scee86bccd27a6ab2/image/i4efe0f36ea709aea/version/1539261184/image.png)