3D Visualisierung komplexwertiger Funktionen
Eine Abbildung
heißt komplexwertige Funktion oder auch komplexe Funktion (die Verwendung der Begriffe ist in der Literatur nicht eindeutig; manchmal wird der komplexwertigen Funktion ein Zusatz angehängt, um zu präzisieren, welche Struktur die Definitionsmenge hat, s. dazu [1]). Hierbei ist die Menge D der Definitionsbereich und die Menge W aller Funktionswerte der Wertebereich der Funktion.
Zerlegt man Argument und Funktionswert von f in ihren jeweiligen Real- und Imaginärteil
z = x + y ∙ i, w = u + v ∙ i mit x, y, u, v ∈ ℝ
so lassen sich u und v als reelle Funktionen der beiden reellen Variablen x und y auffassen:
u = u (x, y) und v = v (x, y).
Mithin ergibt sich eine Abbildung von ℝ² nach ℝ² :
f : D ⊆ ℝ² → W ⊆ ℝ² : (x ,y) ↦ (u, v)
d.h. wir haben es mit vier (!) reellen Variablen zu tun.
Bei einer Funktion f (x, y) mit zwei reellen unabhängigen Variablen lässt sich ein Funktionswert z = f (x, y) als "Höhe" eines Punktes über der x/y-Ebene darstellen, und die Gesamtheit der Funktionswerte bildet eine Fläche (ein "Gelände", engl. landscape) im Raum (s. 3D Flächen). Bei Funktionen mit einer komplexen Variablen hingegen sind die Funktionswerte ebenfalls komplexe Zahlen. Die zuvor beschriebene Art der Darstellung ist nicht möglich – es fehlt einfach eine Dimension.
Außer der im Folgenden auf dieser Seite betrachteten 3D Visualisierung ist auch eine 2D Visualisierung mit Hilfe der Darstellung einer komplexen Zahl in Polarkoordinaten als sogenannte Phasen Plots möglich. Sie finden diese unter 2D Mathe.
Bei der 3D Visualisierung werden die komplexen Funktionswerte f (z) auf reelle Werte heruntergebrochen, d.h. die komplexwertige Funktion f : ℂ → ℂ wird durch die Funktion f̃ : ℝ² → ℝ ersetzt.
In einem 3D Koordinatensystem liegt ein Bereich B ⊆ D in der x/y-Ebene (Gauß'sche Zahlenebene). Auf der z-Achse können dann für z ∈ B dargestellt werden:
-
f̃ (x, y) = ℜe( f (z) ) Realteil von f (z)
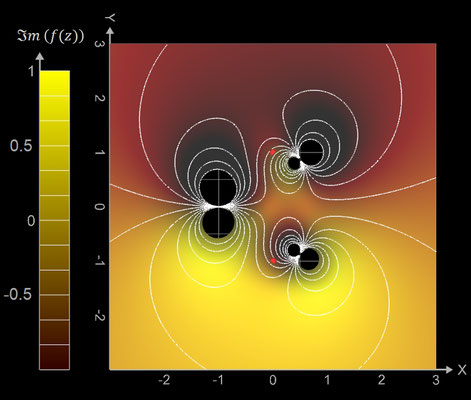
- f̃ (x, y) = ℑm ( f (z) ) Imaginärteil von f (z)
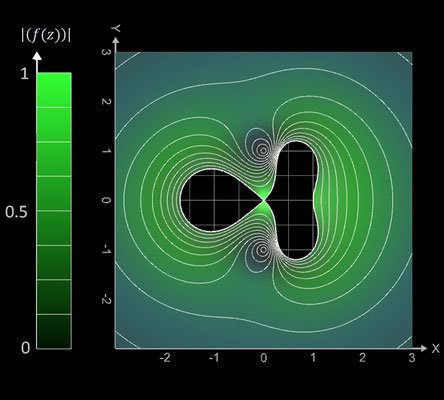
- f̃ (x, y) = | f (z) | Betrag von f (z)
Diese Darstellungen werden nun an einem ersten Beispiel umgesetzt.
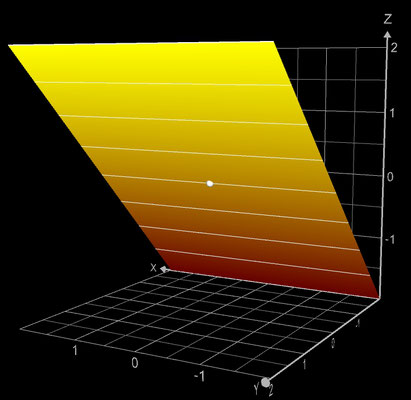
f (z) = z
Für die Funktion f (z) = z (sog. Identität) gilt:
ℜe( f(z) ) = x
ℑm ( f(z) ) = y
Die Funktion hat bei z = 0 eine reelle Nullstelle; in den Grafiken ist diese durch einen weißen Punkt (bzw. "Kügelchen", da ja 3D) dargestellt.
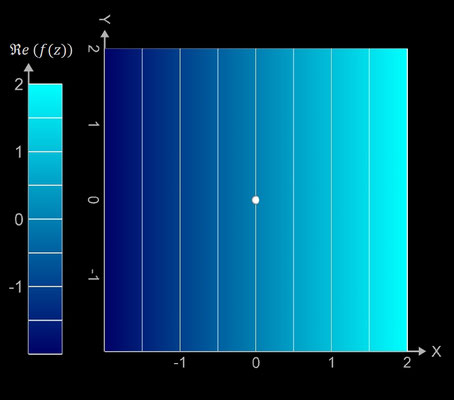
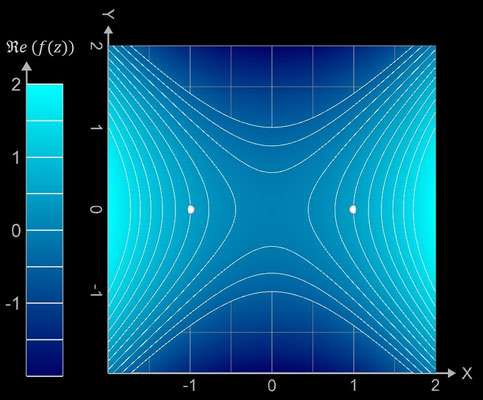
Kontur-Diagramme (Contour Plots)
Eine sinnvolle Ergänzung zu den vorigen 3D Darstellungen einer komplexwertigen Funktion f sind 2D Kontur-Diagramme (Contour Plots). Wiederum liegt der Bereich B ⊆ D in der x/y-Ebene, jedoch eines zweidimensionalen Koordinatensystems. Für ein z ∈ B wird dieser Punkt entsprechend der Art der dargestellten Größe (Betrag, Imaginär-, Realteil, Betrag) anhand einer Skala eingefärbt. Weiterhin werden für die jeweilige Größe wie bei Land- oder Wetterkarten Iso-Linien eingezeichnet. Dies sind Linien mit gleichem Wert der jeweiligen Größe (im 3D Diagramm sind dies Höhenlinien der jeweiligen Größe).
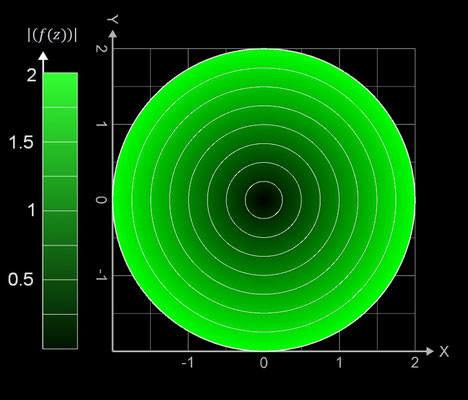
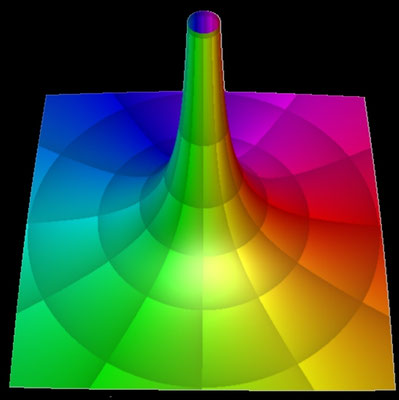
Bezüglich des 3D Plots mit dem Betrag von f (z) gibt es eine Erweiterung:
-
f̃ (x, y) = | f (z) | und (x, y, | f (x+i•y) |) wird entsprechend der Phase an dieser Stelle eingefärbt
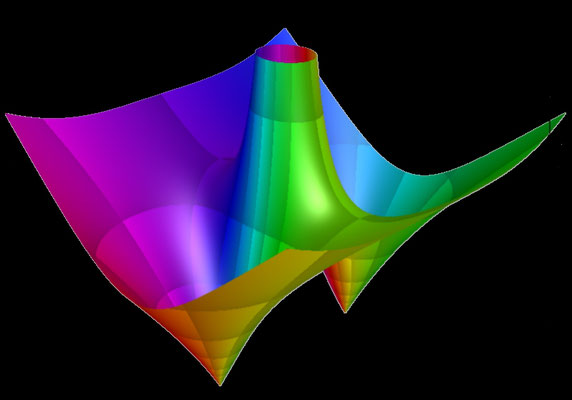
Für f (z) = z ergibt sich dann z.B. die folgende 3D Fläche.
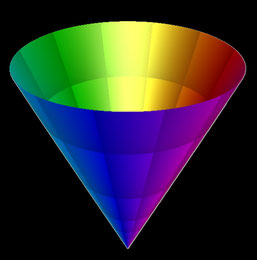
Anmerkung:
In einer der am meisten benutzten Mathematik-Software Wolfram Mathematica ("eier-legende Wollmichsau") wurde die Funktion ComplexPlot3D für die obige Visualisierung erst in 2019 (!) eingeführt [2].
Leider ist sie nicht Bestandteil der kostenlosen Software WolframAlpha. Für meine Belange sind mir bis dato die Lizenzkosten für Mathematica zu hoch; ich habe aber eine interessante Seite gefunden [3], mit der sich online eine derartige Visualisierung erstellen lässt, wohl mit dem kleinen Manko, dass die Achsen mit Skalierung fehlen.
s. auch 2D-Darstellung (Phase Plots) dieser Funktion
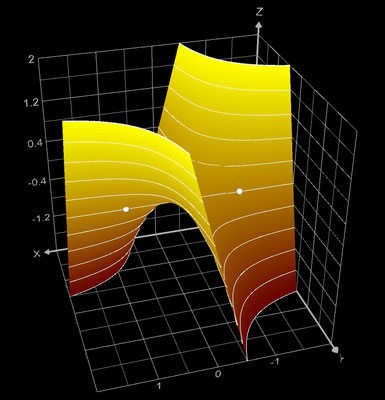
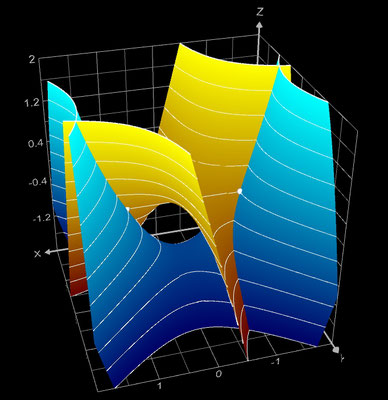
f (z) = z^2 - 1
Die darzustellenden Größen für f (z) = z² - 1 mit z = x + y ∙ i ergeben sich zu:
ℜe ( f(z) ) = x² - y² + 1
ℑm ( f(z) ) = 2 x y
Die Funktion hat bei z = -1 und z = 1 reelle Nullstellen (weiße Punkte bzw. "Kügelchen", da 3D).
Kontur-Diagramme (Contour Plots)
Betrag und Phase
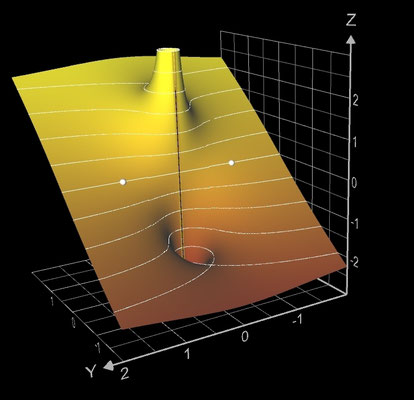
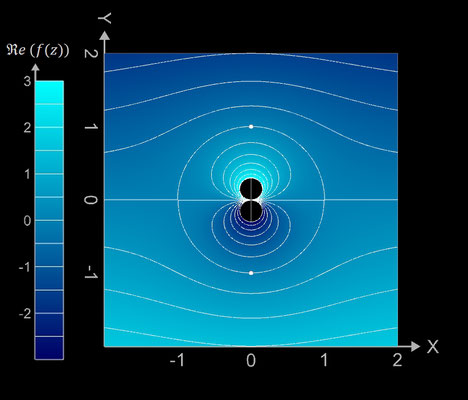
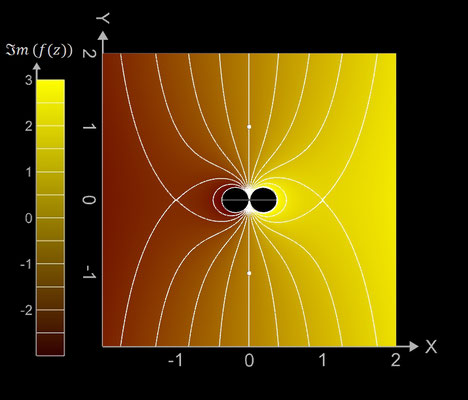
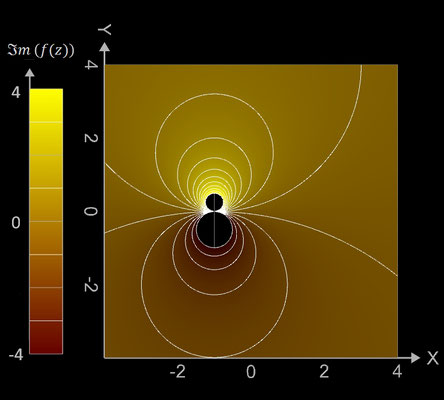
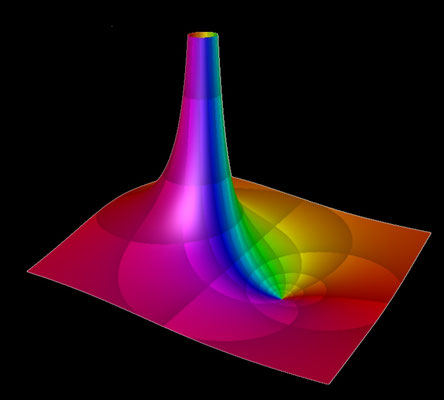
f (z) = 1 / z
Die darzustellenden Größen für f (z) = 1 / z mit z = x + y ∙ i ergeben sich zu:
Die Funktion hat bei z = 0 einen Pol.
Kontur-Diagramme (Contour Plots)
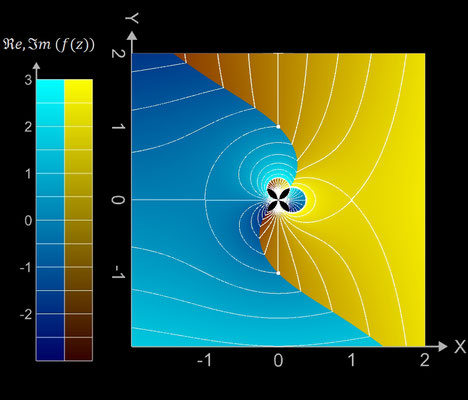
Betrag und Phase
s. auch 2D-Darstellung (Phase Plots) dieser Funktion
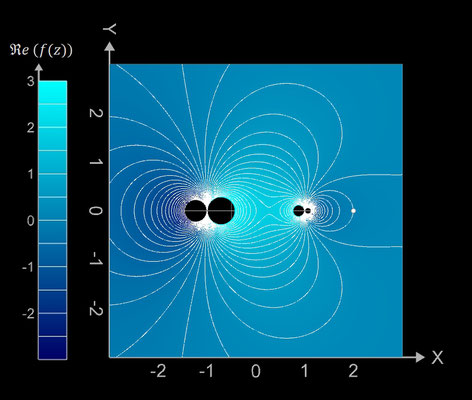
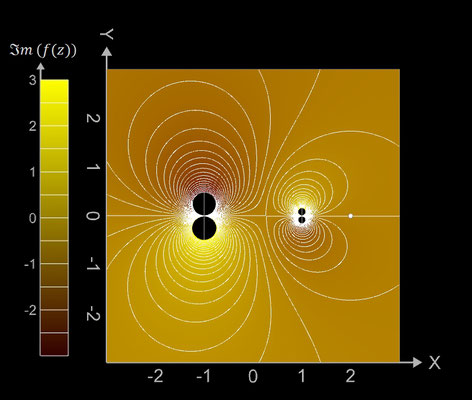
f (z) = i / z - z / i
Für f (z) = i / z - z / i ergeben sich die darzustellenden Größen mit z = x + y ∙ i zu:
Schreibt man den Funktionsterm um:
erkennt man, dass die Funktion die komplexen Nullstellen z = ± i besitzt.
Kontur-Diagramme (Contour Plots)
Betrag und Phase
s. auch 2D-Darstellung (Phase Plots) dieser Funktion
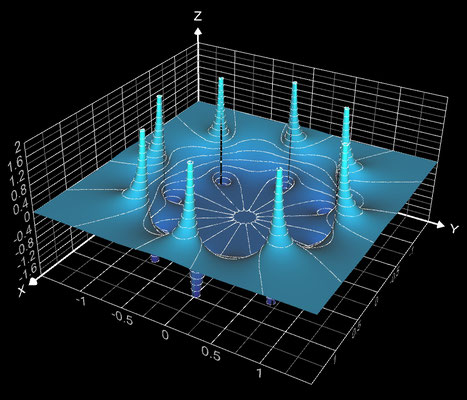
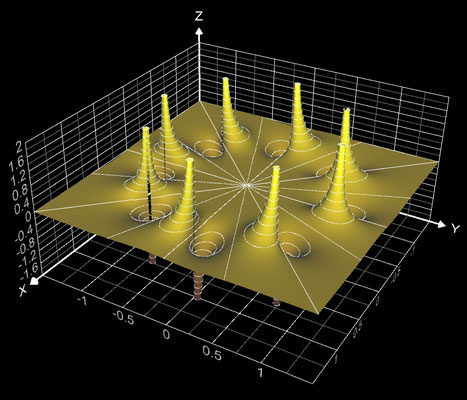
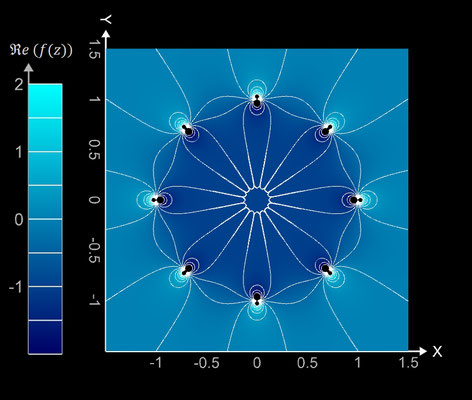
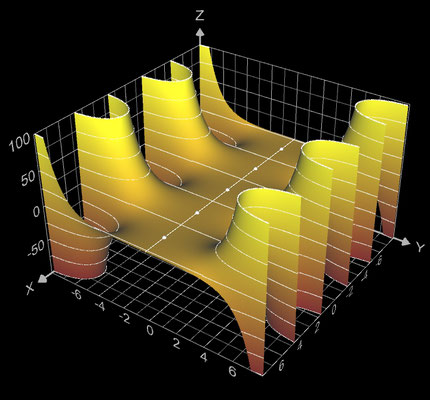
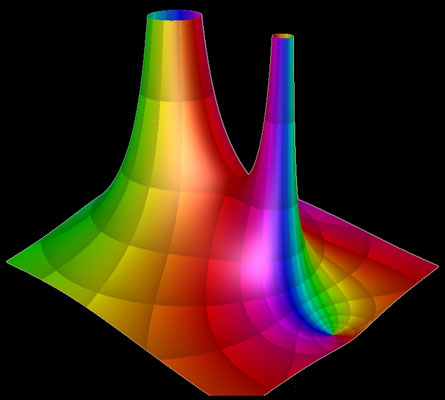
f (z) = 1 / (z^8 - 1)
Die darzustellenden Größen für die Funktion f (z) = 1 / (z^8 - 1) mit z = x + y ∙ i lauten:
ℜe ( f(x) ) = (x8 - 28 x6 y2 + 70 x4
y4 - 28 x2 y6 + y8 - 1) /
(x16 + 8x14y2 + 28x12y4 +
56x10y6 + x8 (70y8 - 2) + 56x6 (y10 + y2)
+ 28x4y4 (y8 - 5) + 8x2y6
(y8 + 7) + (y8 - 1)2)
ℑm ( f(x) ) = (- 8 x y (x6 - 7 x4 y2 + 7 x2
y4 - y6)) /
(x16 + 8 x14y2 + 28x12y4 + 56x10y6 + x8 (70y8 - 2) + 56x6 (y10 +
y2)
+ 28x4y4 (y8 - 5) + 8x2y6
(y8 + 7) + (y8 - 1)2)
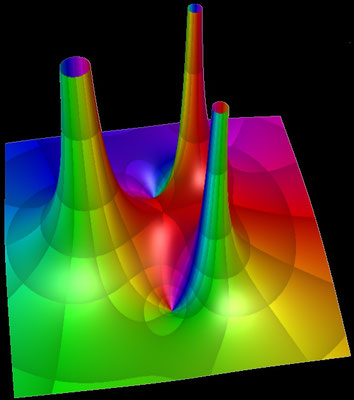
Die Funktion besitzt acht Polstellen bei ± 1, ± i, √½ + ½ i, √½ - ½ i, -√½ + ½ i und -√½ - ½ i.
Kontur-Diagramme (Contour Plots)
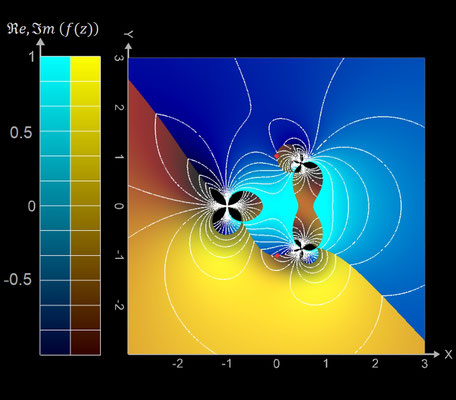
Betrag und Phase
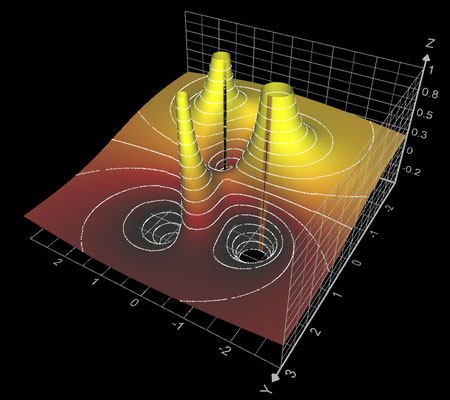
f (z) = (z^2 + 1) / (z^3 + 1)
Mit z = x + y ∙ i lauten für die Funktion f (z) = (z^2 + 1) / (z^3 + 1) die darzustellenden Größen:
Die Funktion besitzt die zwei Nullstellen ± i sowie drei Polstellen bei -1, ½ ± ½ √3 i.
Kontur-Diagramme (Contour Plots)
Betrag und Phase
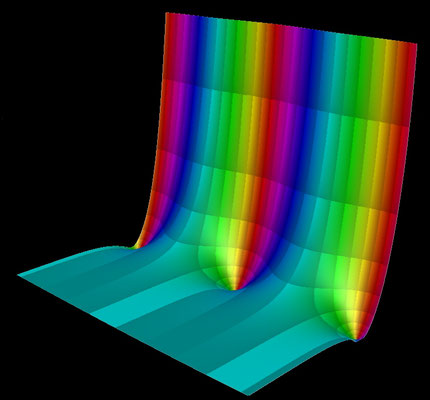
f (z) = exp (z) - 1
Für die darzustellenden Größen für f (z) = exp (z) - 1 mit z = x + y ∙ i ergibt sich:
Die Funktion hat die reellen Nullstellen (0, k∙2π) mit k ∈ ℤ (weiße Punkte bzw. "Kügelchen", da 3D).
Kontur-Diagramme (Contour Plots)
Betrag und Phase
s. auch 2D-Darstellung (Phase Plots) dieser Funktion
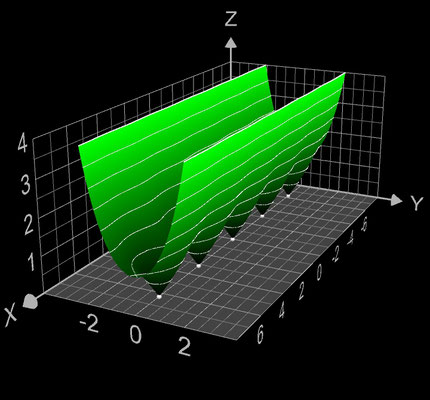
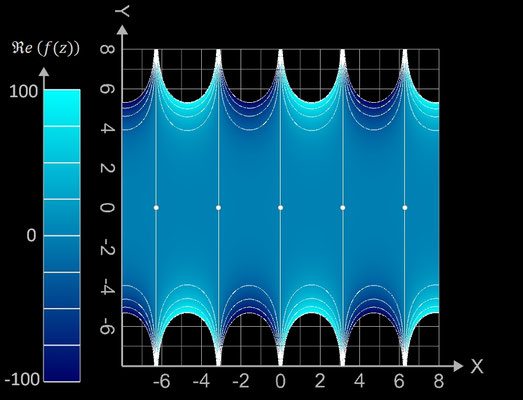
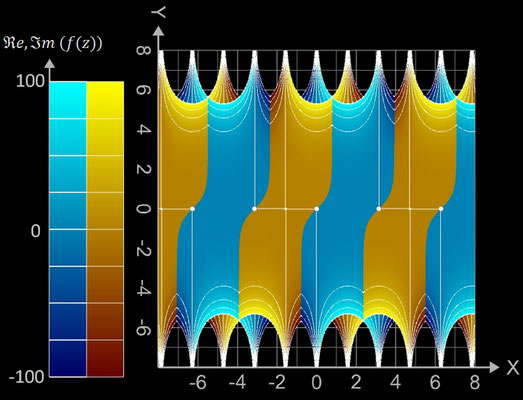
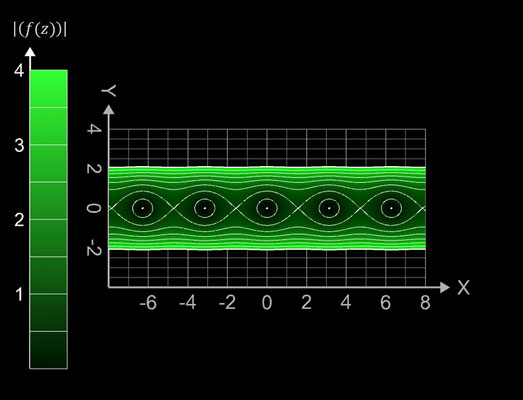
f (z) = sin (z)
Die darzustellenden Größen für f (z) = sin (z) ergeben sich mit z = x + y ∙ i zu:
Die Funktion besitzt die reellen Nullstellen (k∙π, 0) mit k ∈ ℤ ( (weiße Punkte bzw. "Kügelchen", da 3D).
Kontur-Diagramme (Contour Plots)
Betrag und Phase
s. auch 2D-Darstellung (Phase Plots) dieser Funktion
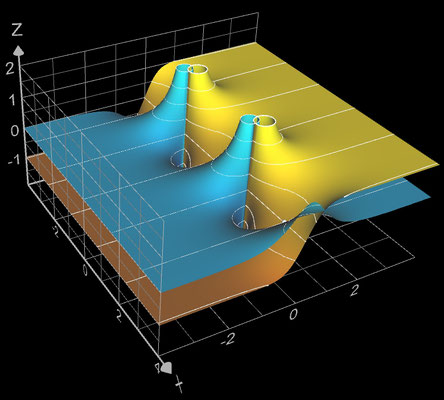
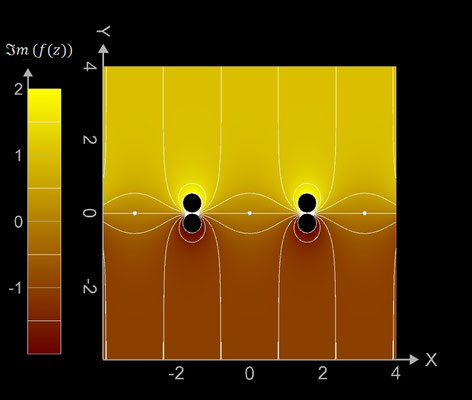
f (z) = tan (z)
Für f (z) = tan (z) = sin(z) / cos (z) lauten mit z = x + y ∙ i die darzustellenden Größen:
Dort, wo sin (z) die Nullstellen hat, nämlich bei (k∙π, 0) mit k ∈ ℤ, hat die Funktion f reelle Nullstellen (weiße Punkte bzw. "Kügelchen", da 3D).
Interessant sind die beiden "Plateaus" beim Imaginärteil ℑm ( tan (z) ). Für deutlich größere bzw. kleinere Imaginärwerte (also y-Werte, da z = x + y i) als 0 ergeben sich zwei Ebenen in der Höhe 1 bzw. -1, denn wie man leicht zeigen kann, gilt
Kontur-Diagramme (Contour Plots)
Betrag und Phase
Im Wikibook zurm Thema "Darstellung komplexwertiger Funktionen" [4] stieß ich auf die Idee, in einer einzigen Grafik den Real- und Imaginärteil einer Funktion in einer Animation fließend ineinander übergehen zu lassen. Hierbei macht man sich zunutze, dass der Imaginärteil Im (z) einer komplexen Zahl z auch als der Realteil der um π/2 im Uhrzeigersinn gedrehten Zahl
aufgefasst werden kann, d.h. es gilt
Animiert man nun
für φ ∈ [0, 2π], so sieht man nacheinander für φ=0 den Realteil, für φ=π/2 den Imaginärteil, für φ=π den negativen Realanteil und für φ=3/2π den negativen Imaginäranteil.
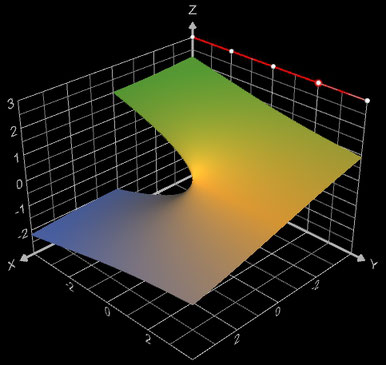
Zwar erschließt sich mir der praktische Nutzen einer derartigen Darstellung nicht so ganz, dennoch habe ich einige Beispiele einmal erstellt. Hierbei stellt die rote Linie eine Skala für φ dar mit den weißen Punkten beginnend bei der z-Achse für die Werte 0, π/2, π, 3/2π und 2π. Der wandernde rote Punkt zeigt den aktuellen Wert von φ an.
f (z) = ( z - 1) / (z + 1)
Mit z = x + y ∙ i
ergeben sich Real- und Imaginärteil von f (z) zu:
Ergänzend hier noch Contour Plots sowie ein Diagramm mit Betrag und Phase der Funktion:
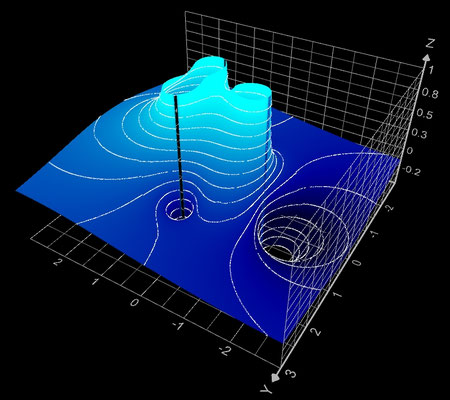
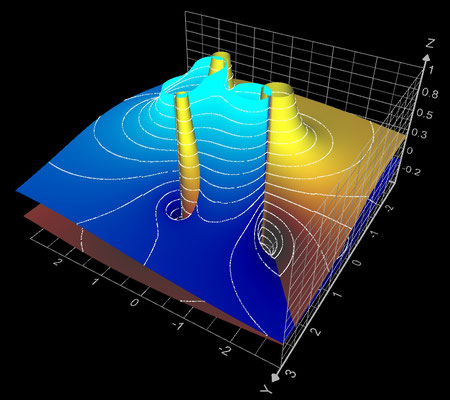
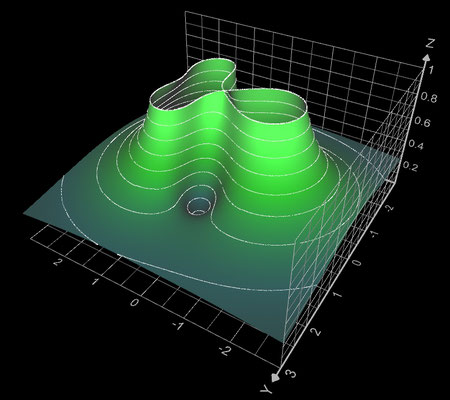
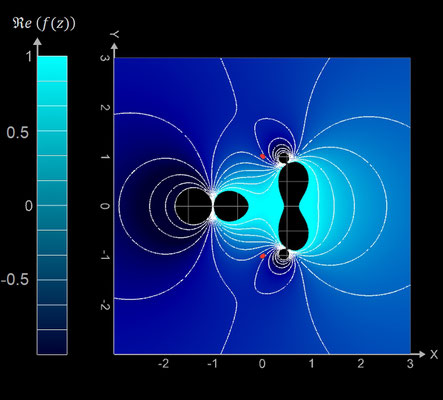
f (z) = (z - 2) / (z^2 - 1)
Mit z = x + y ∙ i
ergeben sich Real- und Imaginärteil von f (z) zu:
Ergänzend sind hier für die Funktion noch Contour Plots sowie der Betrag mit Phase dargestellt:
f (z) = sqrt (z)
Mit z = x + y ∙ i
ergeben sich Real- und Imaginärteil von f (z) zu:
Hinweis: Die senkrechte "Wand" bei x = 0 ist nicht worhanden, sondern ein Artefakt des Graphing Calculator bei Wahl der Darstellungsart "Contour". Für die Darstellungsart "Points" ergibt sich bei genügend großer Punktanzahl eine Darstellung ohne Wand, z.B. für φ=3/2π:
s. auch 2D-Darstellung (Phase Plots) dieser Funktion