Numerische Integration
Ein anderer Weg zum Berechnen von Integralen ist die Numerische Integration. Insbesondere dann, wenn die Stammfunktion schwer hergeleitet werden kann oder gar nicht existiert (s. weiter unten), ist die Numerische Integration der einzige Weg zur Berechnung des Integrals.
Es gibt eine Vielzahl von Verfahren für die Numerische Integration. Eine schnelle und recht genaue Methode, insbesondere geeignet für die Berechnung mit Graphing Calculator 3D, ist die Summierte Simpson Regel (Composite Simpson Rule) [1], [2].
Hierbei wird das Integrationsintervall [a, b] in 2n Teilintervalle aufgeteilt. Für das Integral ergibt sich dann die folgende Näherungslösung:
für i = 0, 1, …, 2n-1.
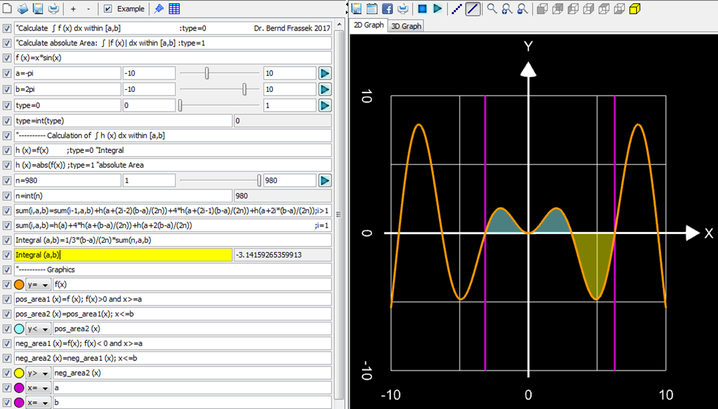
Die obigen Formeln sind in der Graphing Calculator 3D-Datei Integral & Absolute Area.gc3 implementiert:
Programmier-Details:
- Die Summe wird mit Hilfe einer Rekurion über i berechnet mit i = 1 bis n.
- Um den Einfluss von n auf die Genauigkeit zu beobachten, kann n mit einem Slider eingestellt werden.
- Tatsächlich wird die Funktion h (x) integriert; dies erlaubt die Berechnung sowohl des Integrals als auch der absoluten Fläche A, indem die Variable type mit Hilfe eines Sliders eingestellt wird:
Falls f Nullstellen im Intervall [a, b] besitzt, muss dieses nicht gemäß der Nullstellen aufgeteilt werden (s. Integral / Grundlagen); dies erledigt Graphing Calculator 3D automatisch.
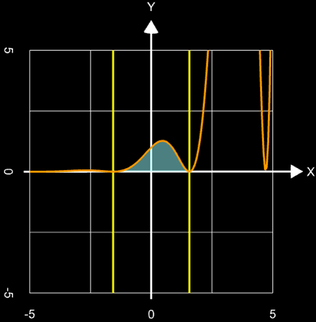
- type = 0 : berechnet das Integral mit h (x) = f (x).
- type = 1 : berechnet die Fläche A mit h (x) = | f (x) |.
-
Zur Darstellung der Stammfunktion kann eine weitere Zeile im Abschnitt
Graphics der Datei hinzugefügt werden
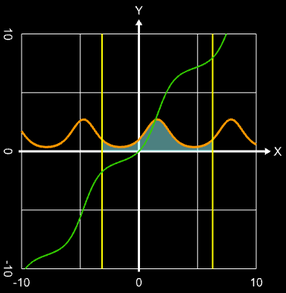
mit folgendem Ergebnis (Stammfunktion in grün):
Für das obige Beispiel f(x) = x sin(x) mit n = 980 und der mathematischen Standardbibliothek Double von Graphing Calculator 3D beträgt der errechnete Integralwert -3.1415926535984022.
Verglichen mit dem exakten Wert -π ergibt dies einen absoluten Fehler kleiner als 10-10, was für die meisten Standardanwendungen ausreichen dürfte.
Numerische Integration - Fehlerabschätzung
Für Polynome bis zum Grad 3 liefert die Summierte Simpson Regel exakte Werte für das Integral, für alle anderen Funktionen liefert es eine Näherung. Der tatsächliche Integralwert ergibt sich somit als Summe der Näherung durch die Simpsonregel S (f) und einem Restglied E (f):
Ist f (x) viermal stetig differenzierbar in [a, b], dann gilt bei der Summierten Simpson Regel für das Restglied
E (f) die Abschätzung [2] :
mit
.
Beispiel 1
Numerisch berechnet werden soll das Integral
dessen Wert sich zu e1 - e0 = 1.781 ... ergibt. Für die Fehlerabschätzung mit n = 20 gilt:
f (4) = ex
Tatsächlich ist der absolute Fehler sogar kleiner; das folgende Diagramm zeigt den entstehenden Fehler bei wachsendem n.
Beispiel 2
Berechnet werden soll das Integral (s. unten)
Für die Fehlerabschätzung mit n = 100 ergibt sich:
Das folgende Diagramm zeigt den Fehlerverlauf bei wachsendem n.
Beispiel 3
Berechnet werden soll die Fläche eines Halbkreises mit dem Radius 1, mithin das Integral
Da die Wurzelfunktion an den Integralgrenzen -1 und 1 nicht differenzierbar ist (dort ist die Steigung -∞ bzw. ∞), lässt sich die obige Abschätzung nicht anwenden.
Das folgende Diagramm zeigt die Entwicklung des Fehlers bis n = 1 000 000.
Bemerkenswert ist, dass Graphing Calculator 3D diese Berechnung in ca. Minute auf meinem PC (s. Tools) leistet; immerhin wurden für das Diagramm 5.5 Millionen Iterationen berechnet.
Numerische Integration - Beispiele
Das Integral kann auch in geschlossener Form mit der Stammfunktion
berechnet werden. Der absolute Fehler mit n = 2000 ist kleiner als 10-13.
Für dieses Integral existiert keine Stammfunktion in geschlossener Form.
Der absolute Fehler ist bereits ab n = 20 kleiner als 10-14.
Der grüne Graph zeigt die Integralfunktion.
Weitere Beispiele für die numerische Integration - insbesondere, da in GC3D keine Integralfunktion implementiert ist - sind enthalten in
- Doppelintegral
- Spezielle Integrale • Integralfunktionen
- Integralanwendungen (Fläche, Schwerpunkt zwischen Funktionsgraphen, Länge Funktionsgraph)
- Rotationskörper (Volumen, Mantelfläche)
- Klothoide, generalisierte Cornu-Spirale