Halley-Verfahren

Vor über 300 Jahren veröffentlichte Edmund Halley 1694 eine Publikation in lateinischer Sprache [1], in der er eine neue Methode zur Berechnung der Nullstellen eines Polynoms vorstellte.
Halley ist bekannt dafür, dass er den nach im benannten Halley'schen Kometen 1682 entdeckte und seine Umlaufbahn berechnete.
Halley verallgemeinerte eine Iterationsformel zur Berechnung der Kubikwurzel einer Zahl und leitete eine Iteration zur Berechnung der Nullstellen eines Polynoms her, wobei er keine Methoden der modernen Analysis verwendete.
Sein Verfahren ist eines der am häufigsten wiederentdeckten Iterationsverfahren in der Literatur. Aufgrund seiner geometrischen Interpretation für reelle Funktionen ist es auch als Methode für tangentiale Hyperbeln bekannt.
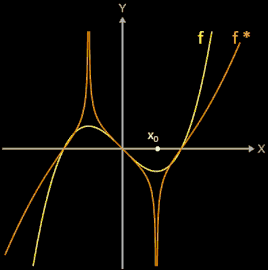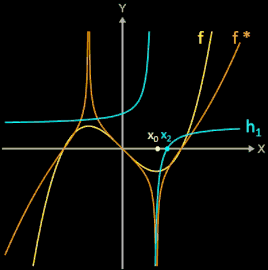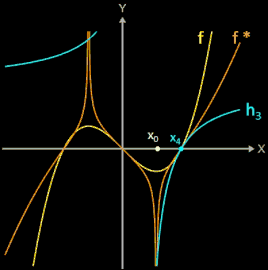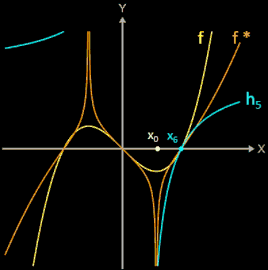
Für eine zweifach stetig differenzierbare Funktion f lautet die Iterationsvorschrift
Außer der ersten Ableitung f ' wie beim Newton-Verfahren wird hier auch die zweite Ableitung f '' benötigt.
Die Iterationsvorschrift lässt sich zum einen herleiten durch eine Taylor-Reihenentwicklung [2], [3].
Alternativ dazu ergibt sie sich, indem man die Funktion f in der Nähe der Nullstelle "gerade biegt" mit Hilfe von
f* (s. orangener Graph in Animation) hat die gleichen Nullstellen wie die zu untersuchende Funktion f.
Wendet man nun auf f* das Newton-Verfahren an, so ergibt sich
woraus die obige Iterationsvorschrift für das Halley-Verfahren folgt.
Eine weitere - und "direkter einsehbare" - Herleitung ist die Idee, die Funktion f an der Nullstelle nicht durch eine Sekante wie beim Sekantenverfahren oder durch eine Tangente wie beim Newton-Verfahren zu approximieren, sondern durch eine Hyperbel, z.B. der Form
Da eine Hyperbel eine Kurve zweiter Ordnung ist, müssen zu ihrer Bestimmung die folgenden Gleichungen an der Stelle xi gelten:
mit den Lösungen
was dann zur Iterationsvorschrift des Halley-Verfahrens führt.
Um für den i-ten Iterationsschritt die Hyperbel hi (x) grafisch darstellen zu können (s. blauer Graph in obiger Animation), werden a, b und c in die obige Hyperbelgleichung eingesetzt; es ergibt sich somit die folgende Funktionsgleichung:
Konvergenzbetrachtungen
Das Halley-Verfahren besitzt eine kubische Konvergenzordnung (einen Beweis findet man bei [3]).
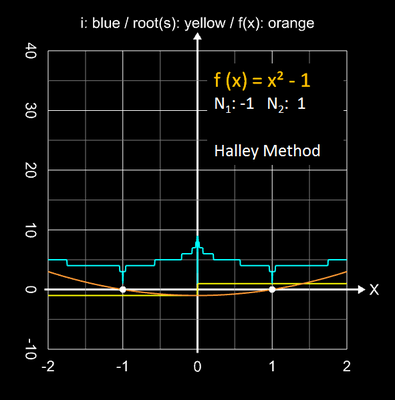
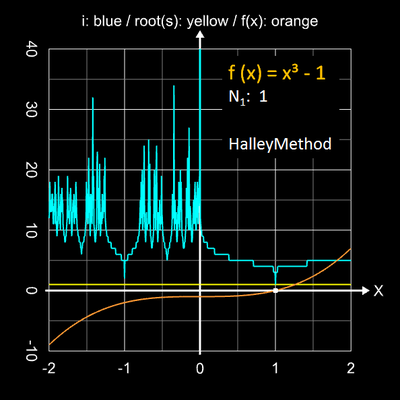
Die folgende Bildsequenz zeigt den Einzugsbereich mit den jeweils erforderlichen Iterationsschritten für eine Genauigkeit von 10-15 für die Funktionen x2-1, x3-1 und x4-1 mit ihren einfachen Nullstellen bei -1 und 1.
Wie auch beim Sekanten- und Newton-Verfahren erhöht sich die Anzahl der Iterationsschritte zum Erreichen der geforderten Genauigkeit deutlich, falls man den Startwert in die Nähe eines Extremwertes der Funktion legt oder es sich bei der gesuchten Nullstelle um eine mehrfache Nullstelle handelt.
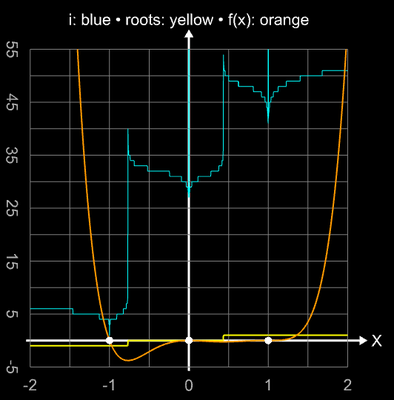
Als Beispiel dafür zeigt die folgende linke Grafik den Einzugsbereich mit den jeweils erforderlichen Iterationsschritten für eine Genauigkeit von 10-15 für eine Funktion mit einfacher bei -1, doppelter bei 0 und dreifacher Nullstelle bei 1 sowie das gleiche für die Funktion f(x) = x4 mit vierfacher Nullstelle (rechte Grafik).
Ebenfalls verschlechert sich das Konvergenzverhalten, falls die Funktion Extremwerte oder Terassen-punkte besitzt und sich der Startwert der Iteration nahe bei diesen befindet. Die folgende Sequenz zeigt dies für die Funktion f (x) = x5 - 10 x + 50 für unterschiedliche Maximalwerte imax der Iterationsschritte bei einer geforderten Genauigkeit von 10-15.
Wendet man das Halley-Verfahren auf das Polynom f (x) = x5 - 3x4 - 5x3 + 15x2 + 4x - 12 oder auf die Funktion f (x) = sin (x) an, so stellt man fest, dass es im Gegensatz zum Sekanten- oder Newton-Verfahren im Bereich zwischen je zwei aufeinanderfolgenden Nullstellen ξk und ξk+1 zu keinen Sprüngen bei der berechneten Nullstelle kommt - das Verfahren liefert "stabil" die Nullstelle im Einzugsbereich nahe der jeweiligen Nullstelle:
Das ist jedoch nicht immer der Fall:
-
Bei der Funktion f (x) =
x4 - x2 - 1 treten Sprünge der berechneten Nullstelle im Bereich innerhalb der
beiden Nullstellen der Funktion auf (s. folgende linke Grafik).
- Bei der Funktion x6 + 7 x3 +x + 1 kommt es zu Sprüngen der berechneten Nullstelle außerhalb der beiden Nullstellen (s. folgende rechte Grafik).
Insbesondere für Polynome lässt sich das Folgende feststellen, wobei in den Grafiken für die Funktion f folgende Punkte farblich markiert:
● Nullstelle
● Extrempunkt ● Wendepunkt ● Terrassenpunkt
Bei einem Funktion mit mindestens zwei aufeinanderfolgenden Nullstellen ξ1 und ξ2 mit ξ1 < ξ2 treten keine mehrfachen Sprünge der berechneten Nullstelle im Intervall [ξ1 , ξ2] auf, wenn in diesem Intervall das Polynom genau einen Extrempunkt besitzt. Folglich weist das Verfahren bei allen quadratischen Funktionen (Parabeln), bei Funktionen des Typs f (x) = a x2n - b, n ∊ |N mit zwei Nullstellen sowie bei reinen Sinus- und Cosinus-Funktionen keine Sprünge auf (vgl. oben für x2, x4 sowie sin(x) ).
Insbesondere bei Polynomen mit mindestens zwei aufeinanderfolgenden Nullstellen ξ1 und ξ2 mit ξ1 < ξ2 treten mehrfache Sprünge der berechneten Nullstelle innerhalb des Intervalls [ξ1 , ξ2] auf, wenn in diesem Intervall die Funktion
- mindestens zwei Extrempunkte oder
- mindestens einen Extrempunkt und mindestens einen Terrassenpunkt besitzt.
Bei einem Polynom mit n ≥ 2 Nullstellen ξ1, ... ,ξn mit ξ1 < ξ2 < ... < ξn treten mehrfache Sprünge der berechneten Nullstelle ausserhalb der Intervalle [ξ1 , ξ2] und [ξn-1 , ξn] auf, wenn die Funktion dort Extrempunkte oder Terrassenpunkte besitzt:
Quellenverweise
[1] https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1694.0029
[2] http://mathworld.wolfram.com/HalleysMethod.html
[3] W. Gander, On Halley's Iteration Method (1985), The American Mathematical Monthly, Vol. 92, No. 2.
(Feb., 1985), pp. 131-134 [PDF]
Download