Spherical Harmonics
Eine interessante Flächenfunktion habe ich bei [1] gefunden. Sie liefert optisch sehr ansprechende und faszinierende, teils "organische", teils "exotische" Flächen in einer unglaublichen Vielfalt. Allgemein werden
diese Objekte als Kugelflächenfunktionen (engl. spherical harmonics) bezeichnet, obwohl sie nur entfernt mit der mathematischen Definition in Zusammenhang stehen, die bei der
Lösung partieller Differential-gleichungen (z.B. in der Physik) zum Tragen kommt.
Die zugrunde liegende Gleichung ist recht einfach:
Sie basiert auf sphärischen (polaren) Koordinaten mit dem Radius r, dem Breitengrad φ und dem Längengrad θ, wobei φ ∈ [0, π] und θ ∈ [0, 2π] gilt.
Die acht Koeffizienten m0 bis m3 und e0 bis e3 bestimmen das Aussehen der Fläche.
Spherical Harmonics - ganzzahlige Koeffzienten
In [1] sind die Koeffizienten m0 bis m3 sowie
e0 bis e3 alle ganzzahlig und größer oder gleich 0, was zu stets
geschlossenen Flächen führt. Ich habe diese Flächen "Typ 1" genannt.
Hinweis: Die Zahlenangaben bei den Bildern
auf dieser Seite sind die Werte der Koeffizienten in der
Reihenfolge m0
m1 m2 m3 |
e0
e1
e2
e3.
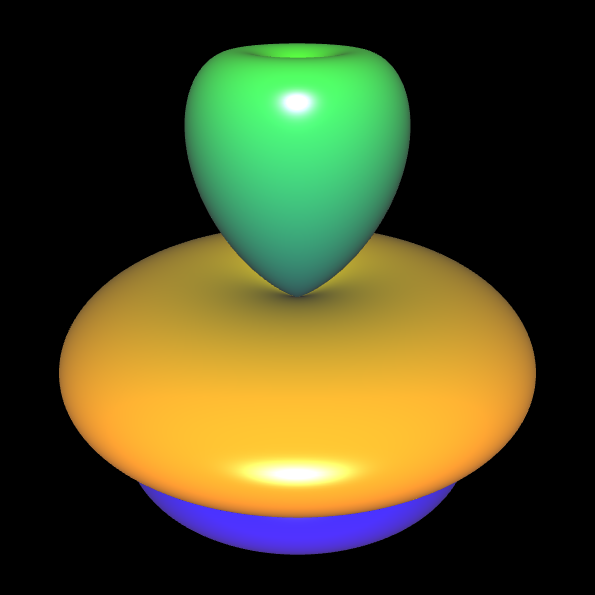
Beschränkt man die zugrunde liegende Gleichung nur auf die φ-Anteile oder auf die θ-Anteile (hierzu reicht es, die Exponenten der auszublendenden Anteile auf 0 zu setzen), so ergeben sich bereits interessante "Basisflächen":
Der wahre "Spaß" beginnt aber erst, wenn sämtliche Koeffizienten beteiligt sind. Beschränkt man die Größe der Koeffizienten m0, …, m3 und e0, …, e3 z.B. auf 10, so gibt es bereits 108 Einstellungen.
Zwar kann man beim Graphing Calculator 3D die Koeffizienten per Slider einstellen, jedoch ist es bequemer, die Koeffizienten zufällig erzeugen zu lassen, wie z.B. für m0:
m0 = int (rand • mmax) wobei mmax die maximale Größe für m0 vorgibt.
Zur Erzeugung einer zufälligen Fläche kann man dann entweder auf "Redraw All" klicken oder - noch viel bequemer - man animiert eine Variable (z.B. mit "Animation Delay" = 1 sec), so dass beim automatischen Hochzählen der Variable jede Sekunde eine neue Fläche erzeugt wird.
Hierbei gibt es jedoch ein Problem: gefällt einem eine Fläche und man stoppt die Animation, um die Fläche dann anders einzufärben oder mit einer größeren Auflösung neu zu berechnen, so ist dies nicht möglich, da mit jedem Klick auf die entsprechenden Werkzeuge die Funktion rand unmittelbar neue Werte annimmt und mit diesen sofort eine neue Fläche erzeugt wird.
Abhilfe bietet hier anstelle der impliziten Funktion rand die Verwendung eines Pseudo Random Number Generator (kurz: PNRG), wie ich ihn auch bei der Simulation eines Galton-Bretts eingesetzt habe. Dieser erzeugt zufällige, jedoch reproduzierbare Zahlen (s. Pseudo-Zufallszahlen). Das obige Beispiel für m0 ergibt sich dann zu
m0 = int (PRNG (i) • mmax) mit i = 0, 1, 2, ...
so dass PRNG mit jedem Wert für i eine neue, aber feste Pseudo-Zufallszahl liefert. Animiert man nun i, kann man die Animation an beliebiger
Stelle anhalten und Einstellungen für die erzeugte Fläche vornehmen. Eine entsprechende Graphing Calculator 3D-Datei zum Download finden Sie unten auf der Seite.
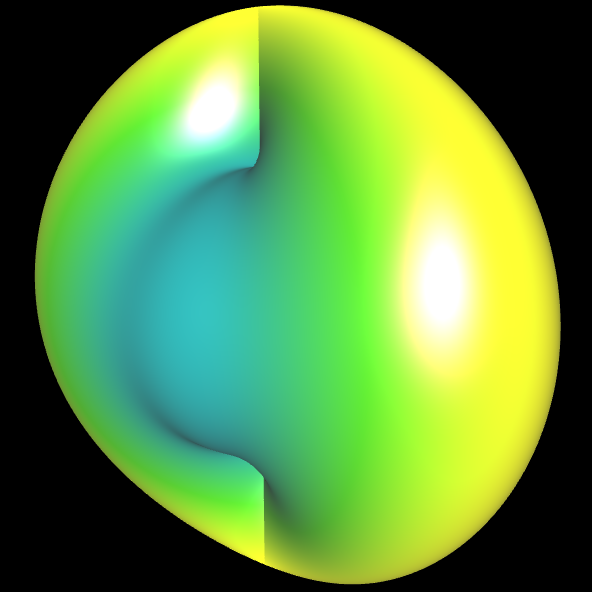
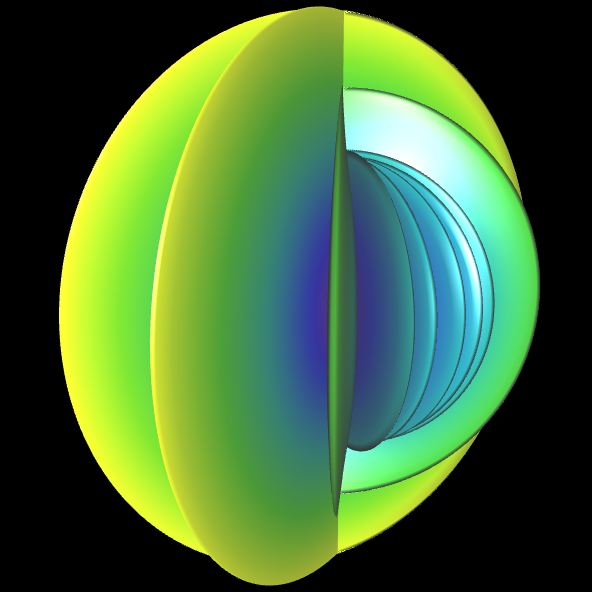
Für viele der folgenden Flächen habe ich Regenbogenfarben dem Zahlenbereich -3 ... 3 zugeordnet. Je nachdem, ob man diese Farbpalette auf r, φ
oder θ anwendet, entstehen nochmals interessante Varianten, wie
das folgende Beispiel zeigt.
In der folgenden Galerie habe ich einige Beispiele für Spherical Harmonics mit ganzzahligen Koeffizienten zusammengestellt, die mit dem Graphics Calculator 3D berechnet wurden.
Spherical Harmonics - Erweiterung mit reellen Koeffizienten
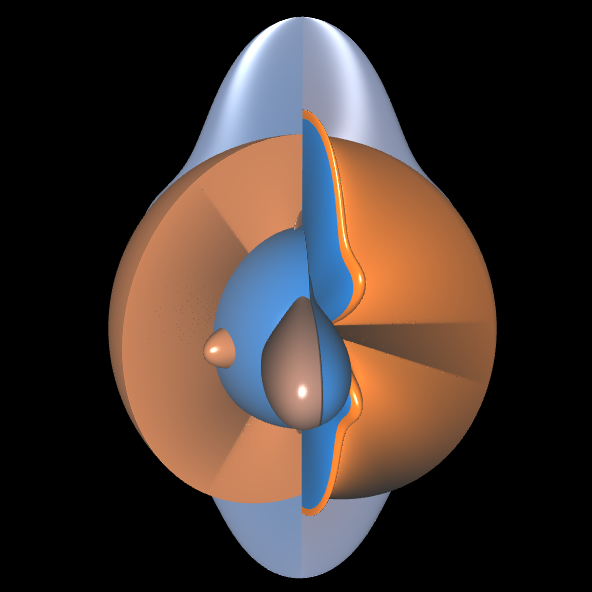
Das Aussehen der erzeugten Flächen lässt sich nochmals deutlich verändern, indem man für die Koeffzienten nicht nur ganze, sondern auch reelle Zahlen zulässt - teils mit überraschenden Ergebnissen bei nur kleinen Änderungen, wie das folgende Beispiel zeigt (linke Fläche: 5731 1111 , rechte Fläche: 5731 111 1.01):
Solange m2 und m3 ganzzahlig ≥ 0 sind, ergeben sich geschlossene Flächen. Insbesondere, wenn e2 und e3 nicht ganzzahlig sind, entstehen "kugelige" Flächen.
Die folgenden Galerie enthält einige Beispiele für geschlossene Flächen mit reellen Koeffizienten (m2 und m3 ganzzahlig ≥ 0).
Offene Flächen entstehen, wenn m2 und m3 nicht ganzzahlig sind. In der folgenden Galerie habe ich dazu einige Beispiele
zusammengestellt.
Die riesige Formenvielfalt lässt sich nochmals erweitern durch folgende Modifikationen:
- Erweiterung des Bereichs für φ auf -π ... π,
- jeden der Sinus- / Cosinus-Terme mit einem Faktor versehen,
- der zugrundeliegenden Gleichung eine additive Konstante hinzufügen,
- andere Einfärbungen ...
... ein schier unendliches Experimentierfeld zur Erzeugung "exotischer" Flächen ...
Insbesondere, wenn man die Flächen mit dem Graphic Calculator 3D erzeugt, kann man diese von allen Seiten und aus anderen Perspektiven betrachten und weitere, teils überraschende Details entdecken. Ich habe bei den obigen Galerien aber bewusst auf sich drehende Bilder verzichtet, um die Dateigrößen klein zu halten.
(Übrigens: auch das kleine blaue, sich drehenden "Logo" oben auf der Seite ist ein Spherical Harmonic).
Zum eigenen Experimentieren finden Sie unten eine Graphic Calculator 3D-Datei ... viel Spaß dabei ...