Kettenlinie
Die Kettenlinie ist in der Physik und Geometrie die Kurve, die eine an zwei nicht übereinander liegenden Punkten aufgehängte idealisierte Kette oder ein Seil unter dem eigenen Gewicht annimmt. Die Form der Kurve hängt von der Lage der Aufhängepunkte und der Länge der Kette, nicht jedoch von ihrem Gewicht ab.
Beispiele aus dem Alltag:
Auch der 192 m hohe (!) Gateway Arch in St. Louis, Missouri (USA) [1] basiert auf einer Kettenlinie, wenngleich er in manchen Schulbüchern als Beispiel für Parabelberechnungen "missbraucht" wird.
Das Problem der Kettenlinie wurde bereits von Galileo Galilei (1564 - 1642) untersucht, jedoch kam er zu dem Schluss, dass die Form der aufgehängten Kette eine Parabel sei. Später wurde dies widerlegt und u.a. von Johann Bernoulli (1667 - 1748), der in 1691 eine korrekte Gleichung herleitete. Weitere historische Details, Quellen sowie weitere Beispiele finden sich in [2].
Auf die physikalische Herleitung der Gleichung für die Kettenlinie soll hier nicht näher eingegangen werden; hierzu sei neben [2] auf folgende Quellen mit gut verständlicher Darstellung verwiesen: [3], [4], [5].
Das Ergebnis für eine idealisierte, d.h. eine nicht dehnbare aber flexible Kette / Seil mit gleichförmiger Massenverteilung, ist die Gleichung
bzw.
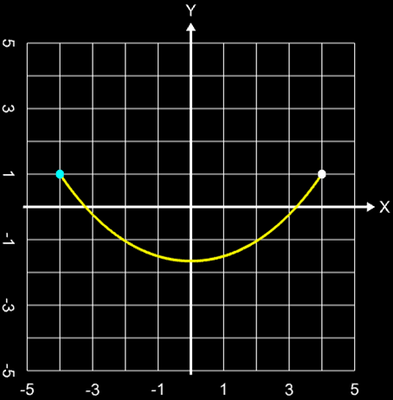
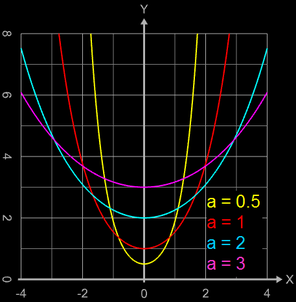
Hierbei bestimmt der Parameter a die Form der Kurve
(s. Grafik), mittels b und c kann diese horizontal bzw. vertikal verschoben werden. Interessanterweise fallen bei der Herleitung der Gleichung die Masse und die Fallbeschleunigung g heraus; ein schweres Seil nimmt
somit dieselbe Form an wie ein leichtes, und auf dem Mond ergibt sich trotz anderer Fallbeschleunigung dieselbe Form wie auf der Erde.

Eine Näherung der Kettenlinie f (x) = cosh (x) durch eine Parabel erhält man, indem man die Taylor-Reihe für ex und e-x anwendet und nach dem 2. Glied abbricht:
Eine sehr viel bessere Näherung (s. Grafik) erhält man mit der
bi-quadratischen Funktion
Weiter unten - nach der nun folgenden Herleitung der Parameter für eine Kettenlinie mit beliebigen Aufhängepunkten - wird gezeigt, welche Form eine Parabel und eine Kettenlinie gleicher Länge und gleicher Aufhängung einnehmen.
Berechnung der Parameter einer allgemeinen Kettenlinie
Ein in der Praxis auftretendes Problem ist die Berechnung der Parameter a, b, c der Kettenlinie für zwei beliebige Aufhängepunkte A ( xA | yA) und B (xB | yB) mit vorgegebener Kettenlänge L.
Für die Länge der Kette gilt (s. Länge Funktionsgraph):
wobei L größer sein muss als die Strecke von A nach B:
Mittels
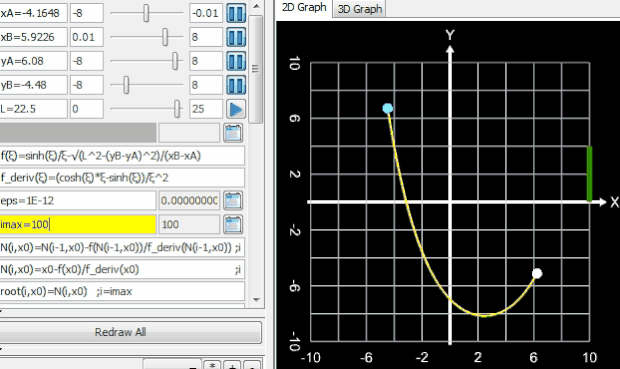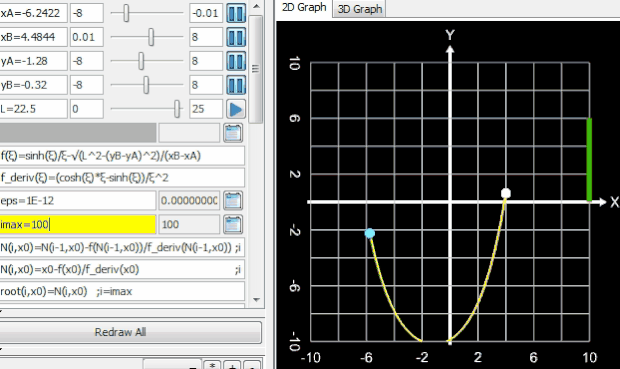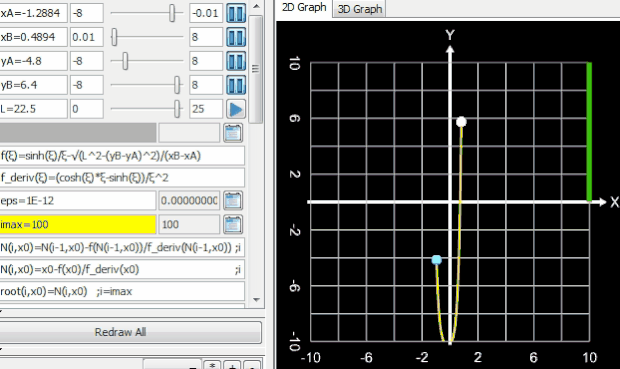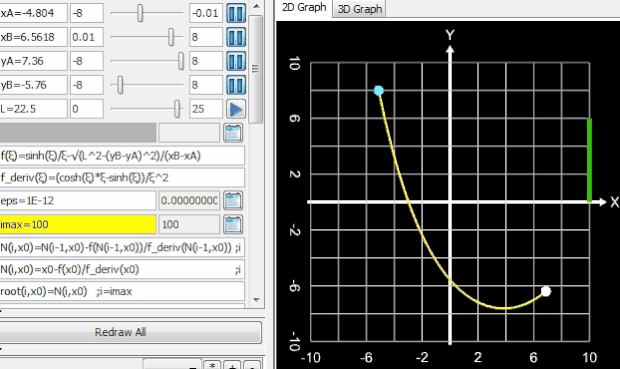
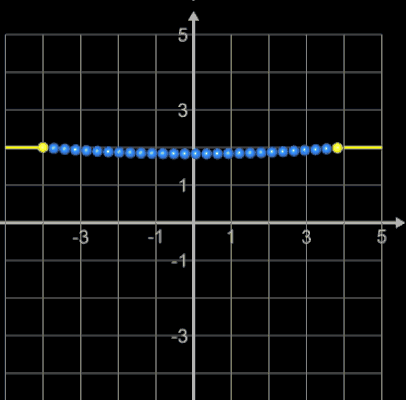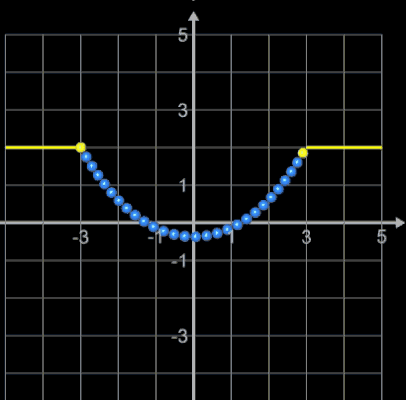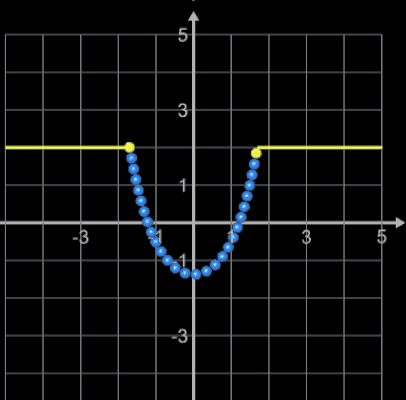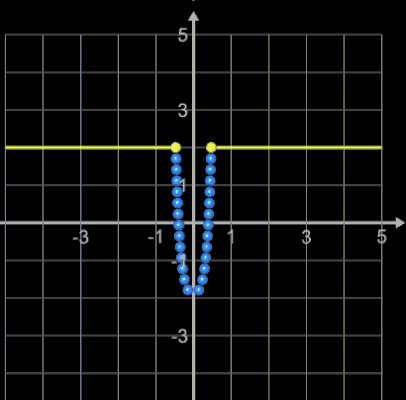
kann der Parameter a numerisch ermittelt werden. Hierzu bietet sich das Newton-Verfahren an. In [4] wird ebenso verfahren und dabei als Startwert ξ0 = 2 verwendet. Dieser Wert dürfte für die meisten praktischen Anwendungen funktionieren, da der Einzugsbereich für das Newton-Verfahren recht groß ist wie etwa in folgendem Beispiel:
Hierbei zeigen die waagerechten gelben Linien den Einzugsbereich, der blaue Linienzug die erforderlichen Iterationsschritte und der gelbe Punkt die Lösung ξfinal an.
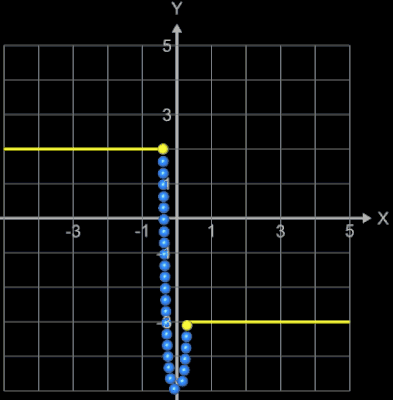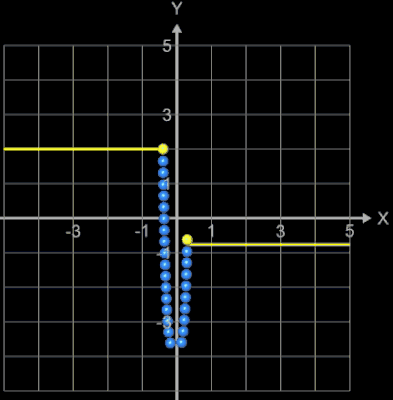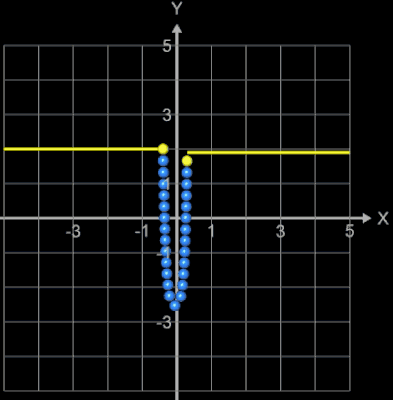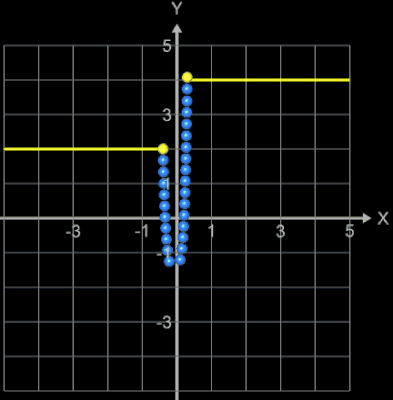
Liegen die Punkte A und B jedoch sehr nah beieinander (im folgenden Beispiel beträgt der horizontale Abstand 0.01, ein in der Praxis wohl eher selten auftretender Fall), so divergiert das Newton-Verfahren für ξ0 = 2. Als Startwert (grüner Punkt) bewährt sich hier wie auch im obigen Beispiel die Vorgabe
Mit ξ = ξfinal können nun die Parameter a, b und c hergeleitet werden gemäß
In [4] werden die Parameter b und c ebenfalls mit dem Newton-Verfahren ermittelt, was jedoch mit den zuvor nach b und c aufgelösten Gleichungen nicht erforderlich ist. Außer einer längeren Rechenzeit für die Iterationen handelt man sich ggf. noch Probleme ein für Wertekombinationen, bei denen das Newton-Verfahren nicht konvergiert.
Die folgende Animation zeigt die berechnete Kettenlinie mit dem Graphing Calculator 3D in Echtzeit. Dabei werden die Parameter a, b und c gleichzeitig animiert. Der grüne Balken am rechten Rand zeigt die jeweils benötigten wenigen Iterationsschritte des Newton-Verfahrens bei einer geforderten Genauigkeit von 10-12 an.
Kettenlinie und Parabel
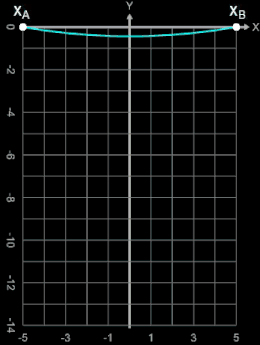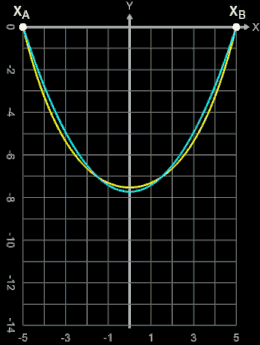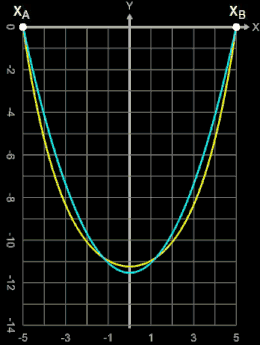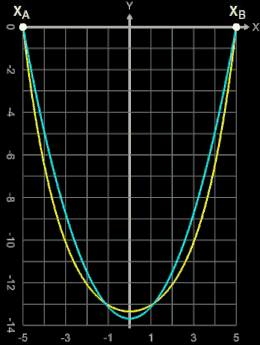
Anhand eines Beispiels mit PA (-5 | 0) und PB (5 | 0) soll gezeigt werden, wie sich die Formen von Kettenlinie und Parabel bei gleicher Kettenlänge L und gleicher Aufhängung unterscheiden.
Die nebenstehende Animation zeigt bei einem Abstand der Aufhängepunkte von 10 für Kettenlängen von 10.05 bis 30.
Mit w = xB lautet die Funktionsgleichung der Parabel
Hierbei wird der Parameter aP solange iteriert, bis die Länge LP des Parabelbogens (s. Länge Funktionsgraph)
gleich der Länge L der Kettenlinie ist.
Gut zu erkennen ist, dass für Kettenlängen, die nur ein wenig größer als der Abstand der Aufhängepunkte sind (bis ca. L = 13), sich Kettenlinie und Parabel kaum unterscheiden. Weitere Vergleiche von Kettenlinie und Parabel finden Sie unter Länge einer Kettenlinie bei Länge Funktionsgraph.
Animationen: Kettenlinien mit Variation von Länge und Aufhängepunkten
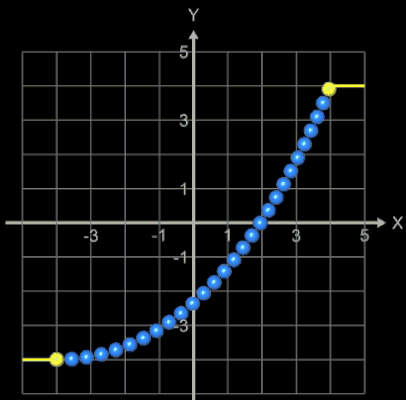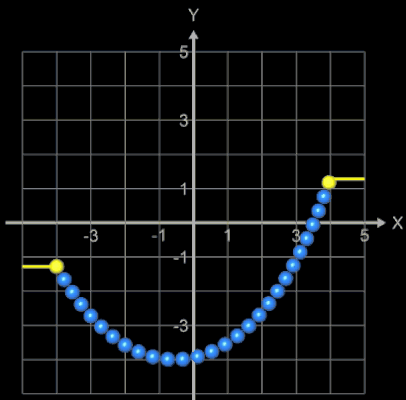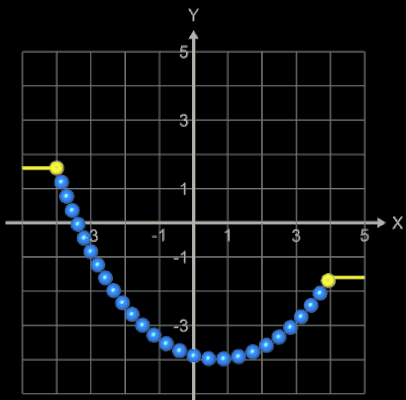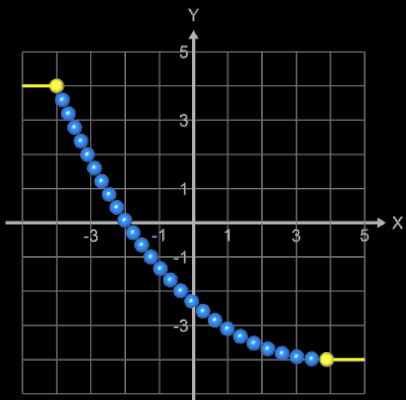
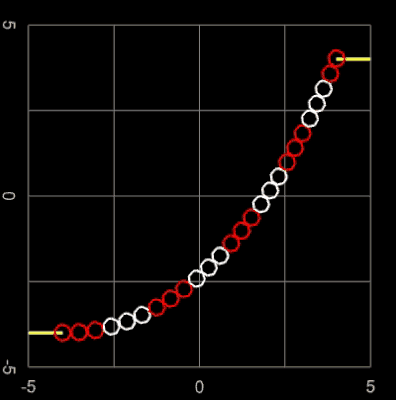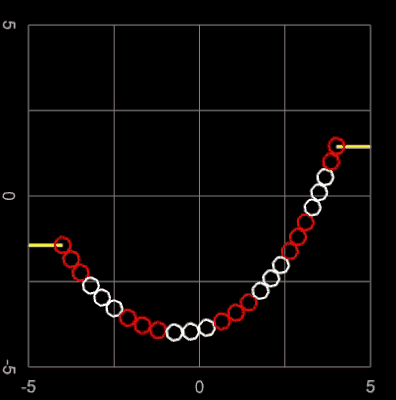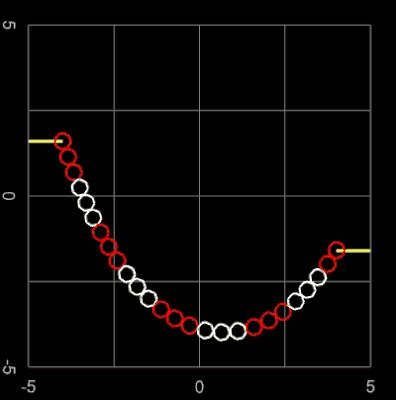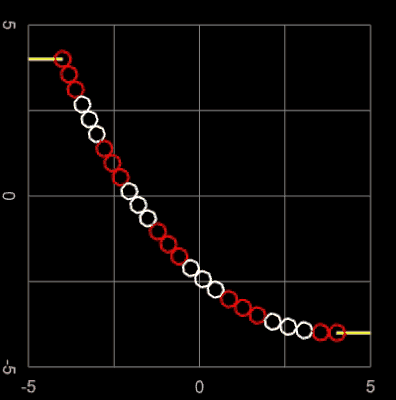
Die folgenden Animationen zeigen die Kettenlinie als 3D-Perlenkette (s. Funktionsgraph aus 3D-Objekten). Hierbei werden bei vorgegebener Kettenlänge L die Positionen der Aufhängepunkte variiert.
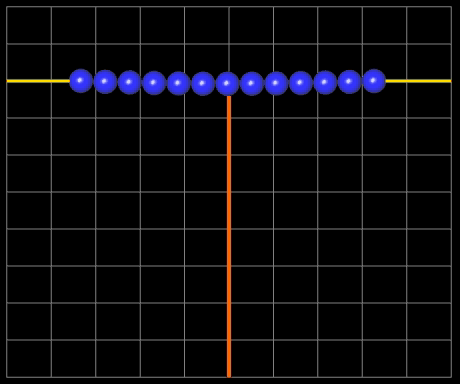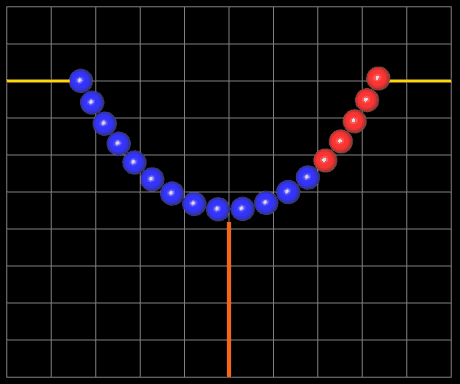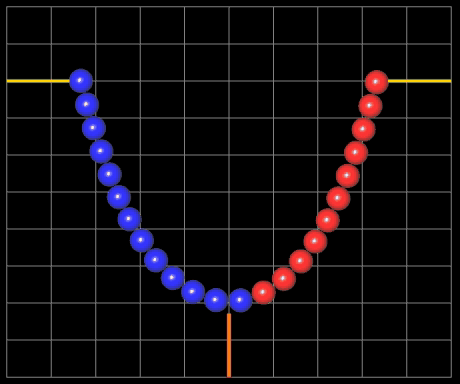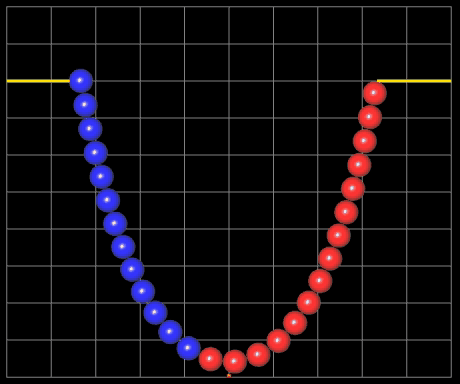
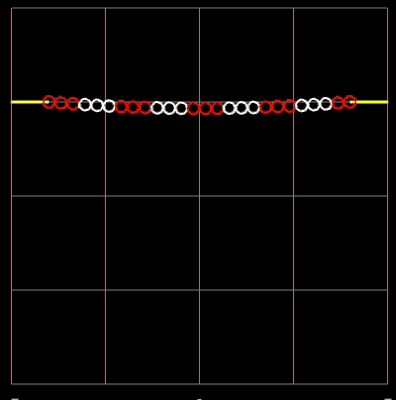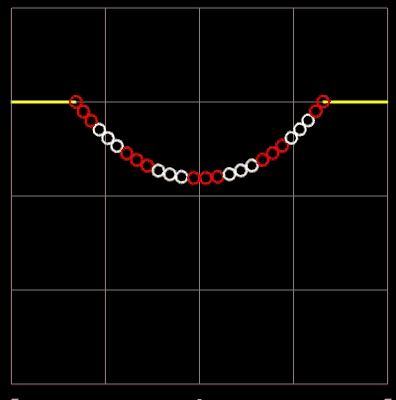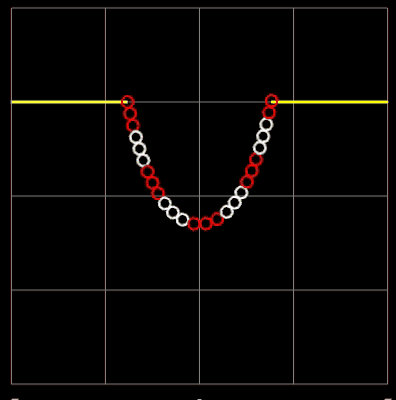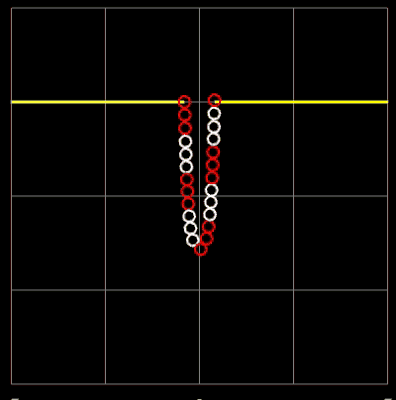
In der folgenden linken Animation wird für zwei feste Aufhängepunkte die Kettenlänge L variiert. Durch die Farbgebung der Kugeln sieht man gut, wie die Länge der Kette zunimmt. Der senkrechte orangene Balken zeigt den resultierenden Durchhang (Abstand Scheitelpunkt zur x-Achse) an.
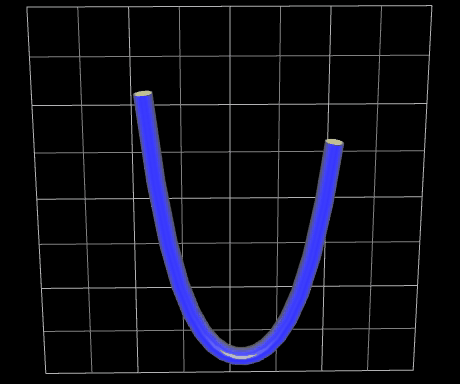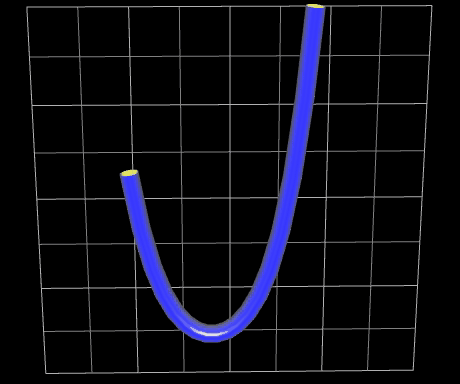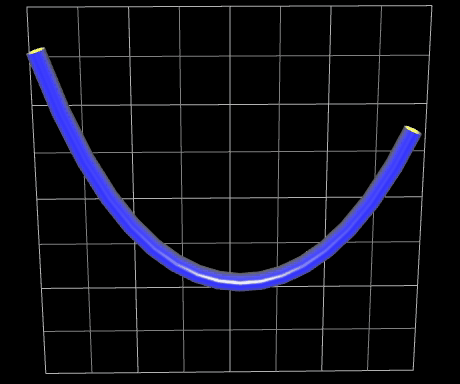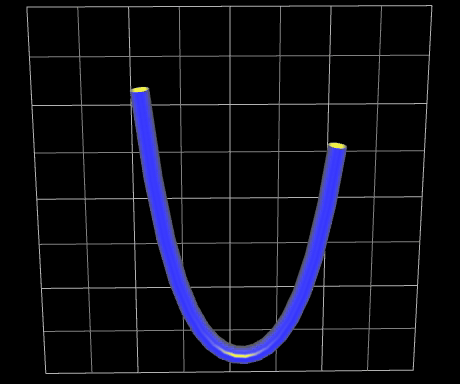
In der rechten Animation ist die Kettenlinie als "weicher, flexibler Schlauch" dargestellt. Dazu wurde die Kettenlinie ummantelt (s. dazu Funktionsgraph als Rohr/Röhre).
Abschließend hier noch 2 pure 2D-Animationen einer Kettenlinie:
Quellenverweise
[1] https://en.wikipedia.org/wiki/Gateway_Arch
[2] https://en.wikipedia.org/wiki/Catenary
[3] http://mathsrv.ku-eichstaett.de/MGF/homes/grothmann/Projekte/Kettenlinie/loesung.html
[4] http://home.eduhi.at/teacher/alindner/Sites/Artikel/Kettenlinie-Arikel.pdf
[5] http://mathforum.org/calcpow/images/catenarytextexact.htm