3D Ei

Ein Ei - im folgenden speziell ein Hühnerei - ist eine interessante biologische "Konstruktion". Es gehört (bei uns) zu den wertvollen Grundnahrungsmitteln und ist in vielen Lebensmitteln enthalten. Hier sollen jedoch weder biologische noch ernährungsphysiologische Aspekte betrachtet werden.
Vielmehr soll die Frage beantwortet werden, wie man ein mathematisches 3D-Modell erzeugt, das dem Original recht nahe kommt.

Auch wenn es die Redewendung gibt "er/sie/es gleichen sich wie ein Ei dem anderen", so stellt man bei genauerer Betrachtung handelsüblicher Eier fest, dass zusätzlich zur Größe (Gewicht) und Farbe es auch bei der Form deutliche Unterschiede gibt; so sind z.B. manche Eier etwas "länglicher", andere hingegen "rundlicher".
Allen Vogeleiern (s. Bild ganz unten) gemeinsam ist aber die Tatsache, dass der Eikörper rotationssymmetrisch um seine Längsachse ist. Es liegt daher nahe, das Ei als Rotationskörper zu modellieren. Im folgenden werden hierzu geeignete Randfunktion mit möglichst wenigen Parametern aufgestellt, die bei Rotation um die x-Achse das Ei entstehen lassen. Abschließend werden diese Modelle mit einem realen Ei verglichen.
Ei-Modell 1
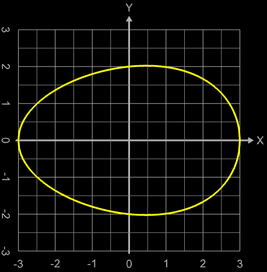
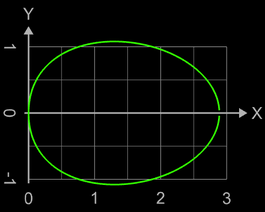
Da ein Ei im Prinzip ein Ellipsoid ist, jedoch mit unterschiedlicher Krümmung an den "Polen", wäre ein erster Ansatz der, als Randfunktion eine Ellipse zu verwenden, die jedoch entsprechend deformiert wird:
Mit a = 3 (halbe Höhe des Eies), b = 2 und c = 0.1 ergibt sich so der Querschnitt des Eies in der Abbildung.
Ei-Modell 2
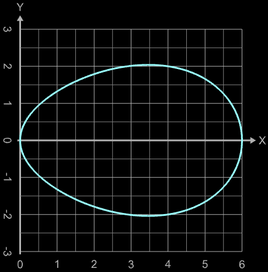
Für meinen Mathematikunterricht, bei dem auch die Volumenberechnung von Rotationskörpern ein Thema ist, habe ich folgende Randfunktion für die Rotation um die x-Achse aufgestellt:
Der Vorteil ist hier, dass das Integral bei der Volumenbestimmung recht einfach zu berechnen ist, da die Wurzel wegfällt und somit nur ein einfaches Polynom zu integrieren ist. Auch die Berechnung weiterer Größen, wie z.B. Integrationsgrenzen (ergeben die Höhe des Eies) und maximaler Durchmesser stellen kein großes Problem dar.
Allerdings ist das entstehende Ei recht "spitz", wie z.B. mit a = 0.5, b= 0.2, c = 7.2 (s. Grafik).
Das folgende Modell ist diesbezüglich etwas flexibler.
Ei-Modell 3
Hier wird im Vergleich zum vorigen Modell der Einfluss der 3. Potenz von x etwas "abgeschwächtt", wodurch u.a. die Spitze etwas runder wird:
Flexibler ist der folgende Ansatz:
Mit b = 1.5 ergibt sich die letzte Gleichung. Die Grafik zeigt die Randfunktion für b = 1.54 und c = 1.15.
Hier noch drei mit den obigen Modellen erzeugten Eierbeispiele:
Ei-Modell 4
Bei diesem Ei-Modell ist der Ausgangspunkt für die Randfunktion ein Kreis mit dem Radius 1, der durch
erzeugt wird. Der konstante Radius 1 wird durch eine Exponentialfunktion mit dem Parameter b ersetzt:
Mit b = 0 ergibt sich ein Kreis, während größere Werte für b diesen deformieren.
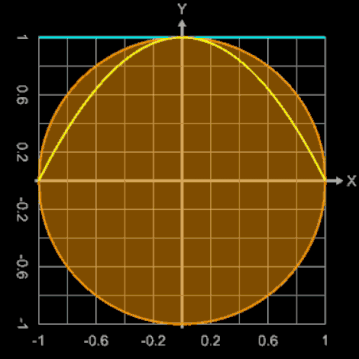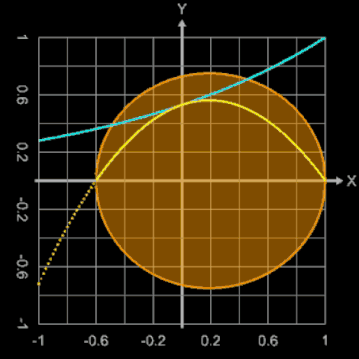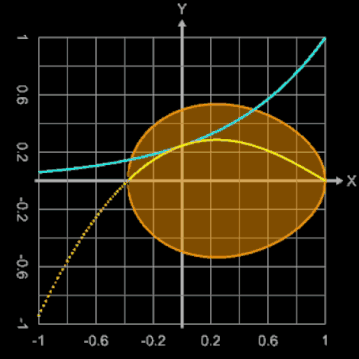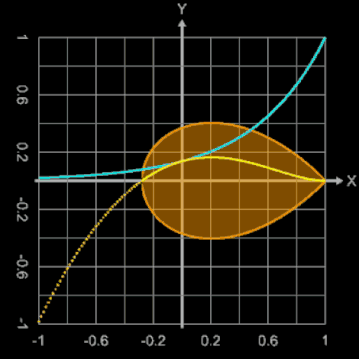
Die nebenstehende Animation zeigt dies für Werte von b zwischen 0 und 2. Dargestellt werden dabei
Brauchbare Werte für die Modellierung eines Hühnereies liegen für b im Bereich zwischen ca. 1.3 und 1.6. Zusätzlich kann mit dem Parameter a
der Graph der Randfunktion gestreckt / gestaucht werden. Das folgende Bild zeigt ein mögliches Ergebnis mit dem Ei-Modell 4, wobei a = 0.9 und b = 1.35 gewählt wurde.
Es liegt nahe, die zuvor aufgeführten Modelleier mit real existierenden Eiern zu vergleichen und auch ein Gütekriterium für die Näherung aufzustellen. Dazu wäre folgendes Vorgehen erforderlich:
- Exaktes Fotografieren (d.h. mit perfekter Ausrichtung der Achsen und Bildebene) verschiedener Eier,
- Normierung der Bilder bezüglich der Größe,
- Ermitteln der Randpunkte eines Eibildes in einem Koordinatensystem
- Bestimmen der Parameter für das Näherungsmodell mit einem geeigneten statistischen Verfahren,
- Berechnen eines Gütekriteriums für die Abweichungen zwischen Ei und Modell.
All dies ist sehr aufwendig, so dass ich lediglich für zwei Eier aus meinem Kühlschrank die Modelle angewendet und dabei die Parameter durch Ausprobieren ermittelt habe:

Dies ist natürlich weder eine wissenschaftliche Herangehensweise noch eine praktikable Methode für das Bestimmen der Parameter. Zum anderen war
der Gegenstand der obigen Betrachtungen lediglich ein Hühnerei. Es gibt jedoch eine große Vielfalt an Formen und Größen bei Vogeleiern, von denen das folgende Bild einige zeigt.
Quelle: www.shutterstock.com
Seit über einem Jahrhundert zerbrechen sich Biologen den Kopf, wie es bei der Bildung des Eies im Eileiter zu dieser Vielfalt kommt, wobei u.a. die Schwierigkeit darin bestand, dass beim Quantifizieren der Eiform keine eindeutige Kenngröße definiert war, die die gesamte Palette an Formen abdeckte.
Seit Mitte des zwanzigsten Jahrhundert haben einige Mathematiker versucht, praktikable Modelle für Vogeleier zu entwickeln. In der interessanten und sehr lesenswerten Publikation [1] geben die Verfasser nach einem ausführlichen und kritischen historischen Rückblick einen allgemeinen Ansatz für ein Modell der Eiform an, das auf einem Kreis beruht, der mittels einer Funktion d (x) entsprechend zur Eiform deformiert wird:
Im Rahmen ihrer Untersuchungen konnten die Verfasser zeigen, dass ein Polynom 3. Grades für d (x) die besten Ergebnisse für alle (!) Eiformen darstellt:
Die Parameter c0, ..., c3 lassen sich intuitiv bezüglich ihres Einflusses auf die Eiforn jedoch nicht leicht interpretieren; daher stellten die Verfasser drei charakteristische Kenngrößen für Vogeleier auf:
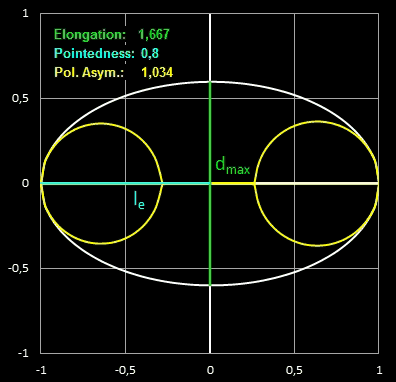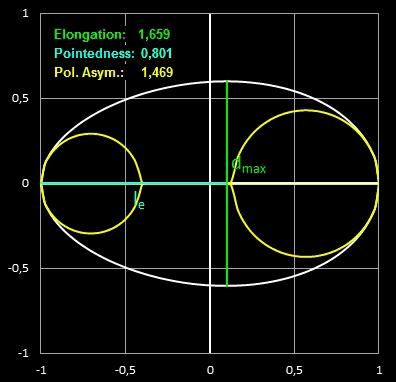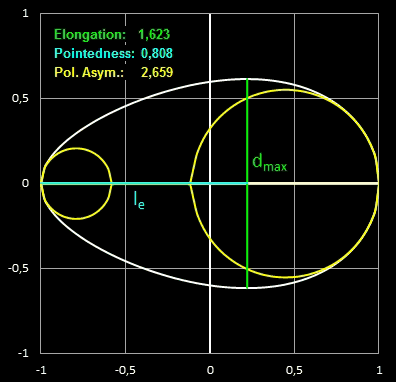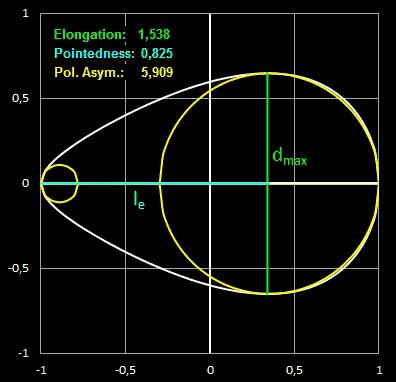
- Elongation (Dehnung) ist das Verhältnis der Länge zum maximalen Durchmesser,
- Pointedness ("Spitzigkeit") ist die Länge vom Punkt, an dem das Ei den maximalen Durchmesser hat, bis zum weiter entfernten Ende, geteilt durch die Gesamtlänge,
- Polar Asymmetry ("Polare Assymetrie") ist das Verhältnis des Durchmessers des größten Kreises, der in den Eiquerschnitt passt und dabei das Ei an seinem stumpfen Pol berührt, zum Durchmesser des größten Kreises innerhalb des Eiquerschnitts, der den spitzeren Pol berührt.
Größere Werte dieser Kenngrößen entsprechen größeren Abweichungen von einer Kreisform. In der folgenden Grafik [1] mit
unterschiedlichen Eiformen verschiedener Vögel kann man den Zusammenhang der Kenngrößen und Eiform gut erkennen.

1 - Braunliest (Halcyon smyrnensis), 2 - Adeliepinguin (Pygoscelis adeliae), 3 - Krauskopfpelikan (Pelecanus crispus), 4 - Rosaflamingo (Phoenicopterus roseus), 5 - Südlicher Streifenkiwi (Apteryx australis), 6 - Zwergtaucher (Tachybaptus ruficollis), 7 - Königsseeschwalbe (Thalasseus maximus), 8 - Königspinguin (Aptenodytes patagonicus), 9 - Fasanblatthühnchen (Hydrophasianus chirurgus), 10 - Trottellumme (Uria aalge)
In den folgenden beiden Animationen werden für verschiedene Eiformen die oben definierten Kenngrößen berechnet:
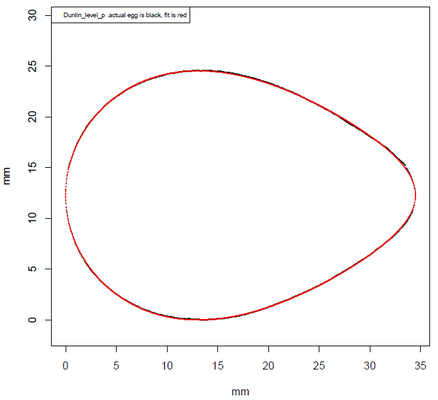
Zur Herleitung der Parameter c0 bis c3 gingen die Verfasser nach dem oben beschriebenen Schema vor. Einige digitalisierte Eibilder, die Herleitung der Modellparameter, einen statistischen Vergleich mit dem Original sowie die verwendeten Programme (Programmiersprache "R") wurden in [2] publiziert.
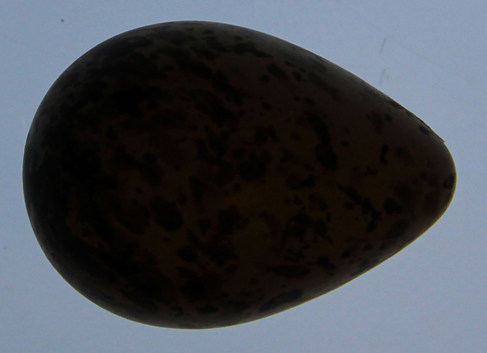
Ich habe aus diesen Daten das Ei des Alpenstrandläufers (Calidris alpina)
herausgepickt. Für x-Werte im Bereich [-1, 1] lauten die Parameter: c0 = 0.68278…, c1 = 0.22139…, c2 = -0.05116…, c3 = 0.03457…
Die folgende Galerie zeigt von links nach rechts: Alpenstrandläufer (www.wikipedia.de), sein Ei (www.wikipedia.de), Eifoto zur Erfassung des Randes ([2]), grafischer Vergleich Rand des Eies mit Modell ([2]) und das von mir mit den obigen Parametern berechnete Ei, versehen mit einem zufälligen Farbmuster (vgl. 3D Texturen unter Meeresschnecken und Muscheln / Modell B. Frassek).
Quellenverweise
[1] Biggins JD, Thompson JE, Birkhead TR (2018), Accurately quantifying the shape of birds’ eggs
[2] https://datadryad.org/resource/doi:10.5061/dryad.8kv2b20