Reuleaux-Dreieck


Ein Reuleaux-Dreieck [1] ist ein Bogendreieck mit konstanter Breite. Es entsteht als Schnittmenge dreier Kreisscheiben mit gleichem Radius r, deren Mittelpunkte jeweils auf der Grenze der beiden anderen liegen.
Benannt ist es nach Franz Reuleaux (1829 - 1905), einem deutschen Ingenieur des 19. Jahrhunderts, der Pionierarbeit auf dem Gebiet der Getriebelehre leistete und in seinen Entwürfen Reuleaux-Dreiecke verwendete [2].
Das Reuleaux-Dreieck ist nach dem Kreis das einfachste nichttriviale Gleichdick, d.h. einer Kurve mit konstanter Breite [3], [4].
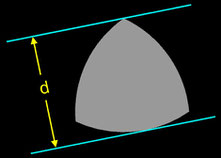
Die Breite einer Kurve ist definiert als der Abstand d zwischen zwei parallelen Geraden, die die Kurve auf gegenüberliegenden Seiten berühren (sog. Stützgeraden).
Beim Reuleaux-Dreieck ist der euklidische Abstand d aller Stützgeradenpaare unabhängig von ihrer Ausrichtung gleich groß.
Während der Kreis das Gleichdick mit der größten Fläche ist, besitzt das Reuleaux-Dreieck die kleinste Fläche. Dazwischen gibt es unendlich viele andere. Mit der Fläche AS des "meniskusförmigen" Kreissegments mit dem Öffnungswinkel α = π / 3 = 60° und der Fläche AD des gleichseitigen Dreiecks mit der Seitenlänge r ergibt sich für die Fläche A des Reuleaux-Dreiecks:
Rotation in einem Quadrat
Das Reuleaux-Dreieck kann eine vollständige Drehung innerhalb eines Quadrats ausführen, wobei es jederzeit mindestens eine der vier Seiten des Quadrats berührt (s. folgende Animation). Aufgrund dieser Eigenschaft wird es manchmal auch als Reuleaux-Rotor bezeichnet, wobei es den Rotor mit der kleinstmöglichen Formfläche darstellt.
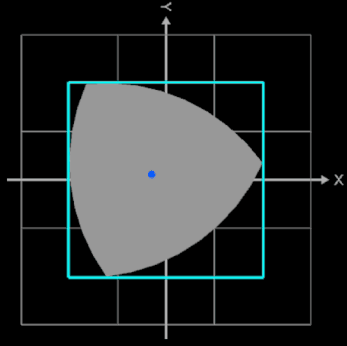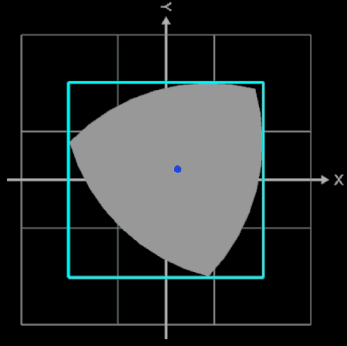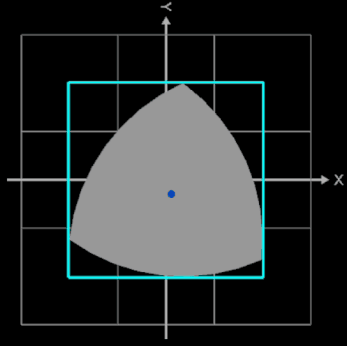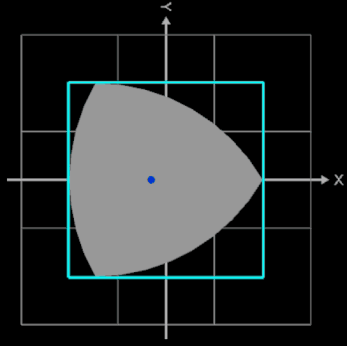
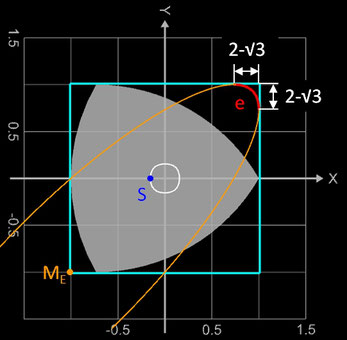
Obwohl dieser bei der Rotation den größten Teil des Quadrats abdeckt, lässt sich auf Grund seines 120°- Winkels ein kleiner Teil des Quadrats im Bereich seiner Ecken nicht abdecken. Nur wenn das Quadrat entsprechend abgerundete Ecken besitzt, berühren bei der Rotation des Reuleaux-Dreiecks stets alle drei Ecken das Quadrat. Dies erreicht man, indem jede Ecke des Quadrats durch ein Teilstück e einer schiefen Ellipse E ersetzt wird, deren Mittelpunkt ME in der diagonal gegenüberliegenden Ecke liegt.
Für ein begrenzendes Quadrat mit der Seitenlänge a = 2 hat die Ellipse
EI in der rechten oberen Ecke
(I. Quadrant des Koordinatensystems, s. obere rechte Grafik) die Parametergleichung [5]
mit der großen Halbachse √3 + 1 und der kleinen Halbachse √3 - 1. Für die Ellipsen der anderen drei Ecken müssen die Vorzeichen entsprechend angepasst werden:
Die bei Rotation des Reuleaux-Dreiecks tatsächlich abgedeckte Fläche des Quadrats beträgt ca. 98.7 % der gesamten Quadratfläche:
Der geometrische Schwerpunkt S des Reuleaux-Dreiecks bleibt bei der Rotation weder an einem einzigen Punkt fixiert, noch bewegt er sich auf einem Kreis. Vielmehr besteht sein Weg aus einer Kurve, bestehend aus vier Ellipsenbögen FI ,.., FIV.
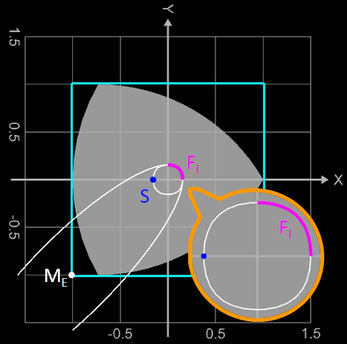
Für ein begrenzendes Quadrat mit der Seitenlänge a = 2 hat die Ellipse FI im ersten Quadranten des Koordinatensystems (s. folgende Grafik) die Parametergleichung
mit der großen Halbachse 1 + 1 / √3 und der kleinen Halbachse 1 - 1 / √3 . Für die Ellipsen der anderen drei Bögen müssen die Vorzeichen entsprechend angepasst werden:
Bei einer vollständigen Rotation von 360° des Reuleaux-Dreiecks durchläuft sein Schwerpunbkt S die vier Ellipsenbögen FI ,.., FIV insgesamt dreimal!
Um dies besser verfolgen zu können, wurde in der obigen Animation eine fixierte Gerade vom Schwerpunkt S zu einer Dreiecksspitze eingezeichnet.
Anwendungen
Nachfolgend sollen zwei Anwendungen des Reuleaux-Dreiecks betrachtet werden.
Wankelmotor
Der Wankelmotor [6] ist ein Rotationskolbenmotor, der nach seinem Erfinder Felix Heinrich Wankel (1902 - 1988) [7] benannt worden ist.
Bei einem Wankelmotor wird die Verbrennungsenergie ohne den Umweg einer Hubbewegung, wie es bei Hubkolbenmotoren der Fall ist, direkt in eine Drehbewegung umgesetzt.
Ein dreieckiger Rotor rotiert in einem doppelbogigen Gehäuse und berührt dabei ständig die Gehäusewand. Die Gehäuseform hat annähernd die Form eines an der langen Seite eingebuchteten Ovals und ist eine Epitrochoide [8] mit einem Verhältnis der Radien vom Grund- zum Abrollkreis von 2:1. Die Kontur des Kreiskolbens hat annähernd die Form eines Reuleaux-Dreiecks.

Quelle: mazda.com
Der Wankelmotor arbeitet nach dem Viertaktprinzip. Die in den Räumen zwischen den Rotorflanken und dem Gehäuse transportierten Gasmengen durchlaufen abwechselnd die vier verschiedenen Phasen/Takte Ansaugen - Kompression - Expansion - Ausstoßen [9].
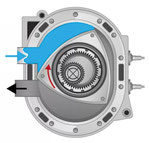
ANSAUGEN
Während dieser Phase saugt ein durch die Bewegung des Rotors verursachter Druckabfall das Kraftstoff-Luft-Gemisch in die kalte Kammer an. Durch die Rotation des Rotors wird das Gemisch in den zweiten Takt des Zyklus gedrückt.
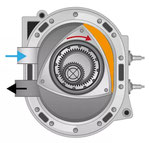
KOMPRESSION
Bei weiterer Drehung des Kolbens nimmt das zwischen Rotor und Gehäuse eingeschlossene Volumen ab, wodurch das Kraftstoff-Luft-Gemisch verdichtet wird.

EXPANSION
Wenn das Gemischvolumen minimal ist, lösen eine oder mehrere Zündkerzen die Verbrennung aus, was zu einem raschen Druck- und Temperaturanstieg führt. Die plötzliche Expansion des nun gasförmigen Kraftstoffgemisches dreht den Rotor und den Exzenter weiter.
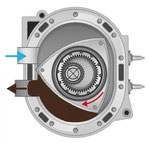
AUSLASS
Die expandierenden Abgase verlassen die Kammer durch den im vierten Takt geöffneten Auslasskanal. Bei weiterer Rotation des Kolbens wird der Auslasskanal geschlossen, während sich der Einlasskanal wieder öffnet, um einen neuen Zyklus zu beginnen.
Im Folgenden noch einmal das Ganze als Animation, die auf einem von mir editierten Film von CARinfoD [10] beruht. In der Zeit, in der sich der Dreieckskolben einmal vollständig dreht (rote Markierung), dreht sich die exzentrische Welle genau dreimal (orangefarbige Markierung, s. auch oben bei Drehung des Reuleaux-Dreiecks im Quadrat).
Bohrer für quadratische Löcher
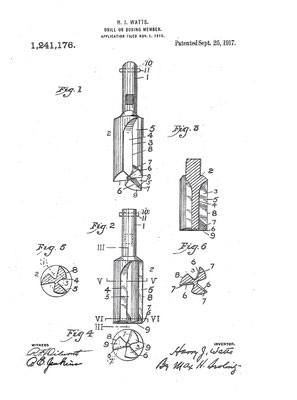
Im Jahr 1917 wurde Harry J. Watts das US Patent 1,241,176 erteilt (s. folgende Bilder). Darin beschreibt er einen speziellen Bohrer in Form eines Reuleaux-Dreiecks, modifiziert mit konkaven Aussparungen, um Schneidflächen zu bilden. Wird der Bohrer in einem speziellen Spannfutter montiert, welches ermöglicht, dass der Bohrer keinen festen Drehpunkt hat, kann er ein Loch bohren, das nahezu quadratisch ist.
Eine schöne Animation, die die Arbeitsweise des Bohrers verdeutlicht, habe ich auf der Seite Mathematical Etudes eines russischen Teams gefunden [11]:
Das Reuleaux-Dreieck findet man auch in gotischen Kirchenfenstern, wie z.B. bei der Liebfrauenkirche in Brügge (Belgien) [5]. Auch unter den Gitarrenplektren gibt es manche, die ein Reuleaux-Dreieck als Kontur haben [12].
Auch manche Buntstifte haben einen Querschnitt ähnlich einem Reuleaux-Dreieck (Foto: Tatiana Mirlin/ Shutterstock). Beim Kölntriangle, einem ca. 103 m hohem Gebäude mit 29 Etagen [13 ] findet man einen Grundriss mit bogenförmigen Kanten, ähnlich einem Reuleaux-Dreieck (Foto: webbaviation.de).
"Fake"-Reuleaux-Dreieck
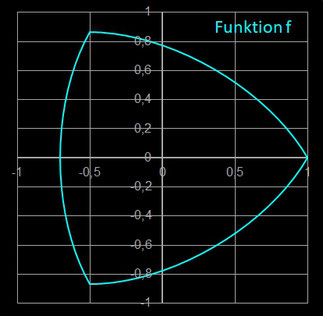
Bei der Internet-Recherche zum Thema "Reuleaux-Dreieck" stieß ich auf einen Beitrag in Mathematics Stack Exchange [14] in dem ein Benutzer die Frage stellt, ob es sich bei dem durch die folgende Funktion f generierten Objekt um ein Reuleaux-Dreieck handelt:
Betrachtet man die Grafik dazu, ist man wirklich schnell geneigt, es für ein Reuleaux-Dreieck zu halten:
In der folgenden Grafik wurde zusätzlich ein "echtes" Dreieck (Bogenradius r = √3) in weiß eingezeichnet. Man sieht sofort, dass das auf der Funktion f basierende Dreieck etwas kleiner ist:

Wäre der Graph von f ein Reuleaux-Dreieck, so müssten die eingezeichneten Radien r1 und r2 gleich groß sein. Dies ist jedoch nicht der Fall, wie die folgende Rechnung zeigt:
Punkt A: f (0) = 1
Punkt B: f (π/2) = ω = -½ + i ½ √3
Punkt C: f (3/4 π) = ω cos (π/4) + ω² cos (π/4) = ½ √2 (ω + ω²)
= ½ √2 (-½
+ i ½ √3 +
¼ - 2•½ i ½ √3 - ¾)
= ½ √2
(-1) = - ½ √2
| r1 | = √ [ (1-(-½))² + (-½ √3)² ] = √ [ 9/4 + ¾ ] = √3 ≈ 1,73205081..
| r2 | = √ [ (1-(- ½ √2))² ] = 1 + ½ √2 ≈ 1,70710678..
Gleichdick ähnlich einem Reuleaux-Dreieck
Das Reuleaux-Dreieck ist ein Gleichdick, hat aber Spitzen und ist somit stückweise "glatt" (engl. smooth), d.h. es gibt nicht differenzierbare Bereiche (eben an den Spitzen). Man könnte nun vorschnell annehmen, dass der Kreis die einzige Kurve mit konstanter Breite ist, die auch analytisch ist, d.h. deren Ableitungen überall existieren.
Dies ist jedoch nicht der Fall. Tatsächlich sind mehrere Methoden zum Konstruieren geschlossener Polynome in zwei Variablen (x, y) bekannt, deren Nullmenge Kurven konstanter Breite in der Ebene definiert. In [15] konstruiert der Verfasser ein solches Polynom 8. Grades:
(x²+y²)4 - 45(x²+y²)3 - 41283(x²+y²)² + 7950960(x²+y²) + 16(x²-3y²)3 + 48(x²+y²)(x²-3y²)²
+ (x²-3y²)x(16(x²+y²)²-5544(x²+y²)+266382)-720³ = 0
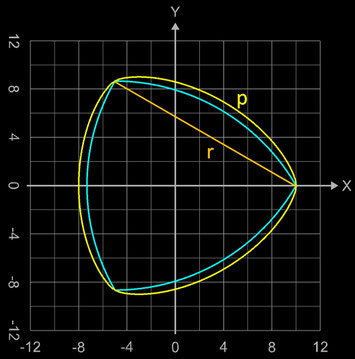
Das Polynom p (gelb in folgender Grafik) hat die Nullstellen x1 = 10, x2 = - 8 und somit die Breite 18; ebenfalls ist ein Reuleaux-Dreieck eingezeichnet mit einer Weite von r = 10 √3.
Sein Polynom ist sehr kompliziert im Aufbau, und so stellt er selbst folgende Fragen auf:
- Existiert ein Polynom mit einfacherer Form?
- Existieren Polynome mit niedrigerem Grad?
- Welchen minimalen Grad hat ein Polynom, dessen Graph eine Kurve konstanter Breite ist?
Diese allgemeinen Fragen scheinen weiterhin ein Bereich aktiver Forschung zu sein. So wiesen in 2013 die Verfasser in [16] nach, dass der Grad 8 der kleinstmögliche Grad für ein derartiges Polynom ist.
Quellenverweise
[1] https://en.wikipedia.org/wiki/Reuleaux_triangle
[2] https://de.wikipedia.org/wiki/Franz_Reuleaux
[3] https://de.wikipedia.org/wiki/Gleichdick
[4] https://en.wikipedia.org/wiki/Curve_of_constant_width
[5] https://mathworld.wolfram.com/ReuleauxTriangle.html
[6] https://de.wikipedia.org/wiki/Wankelmotor
[7] https://de.wikipedia.org/wiki/Felix_Wankel
[8] https://en.wikipedia.org/wiki/Epitrochoid
[9] https://www.wankelsupertec.de/
[10] https://www.youtube.com/@carinfo3d-En/videos
[11] https://etudes.ru/etudes/drilling-square-holes/
[12] https://www.vip-guitar.de/shop/VIP-Guitar-Plektren-c118750072
[13] https://de.wikipedia.org/wiki/K%C3%B6lntriangle
[14] https://math.stackexchange.com/questions/4311123/is-this-graph-a-reuleaux-triangle
[15] S. Rabinowitz (2013) A Polynomial Curve of Constant Width, Missouri Journal of Mathematical
Sciences, 9 (1997) 23–27, DOI: 10.35834/1997/0901023
[16] M. Bardet, T. Bayen (2013) On the degree of the polynomial defining a planar algebraic curves of
constant width, arXiv:1312.4358