Dandelin'sche Kugeln
Die Dandelin'schen Kugeln sind ein geometrisches Hilfsmittel zum Nachweis (s. dazu [1]), dass der ebene Schnitt eines Drehkegels ein regulärer Kegelschnitt [2] ist, sofern die Schnittebene nicht durch die Spitze verläuft.
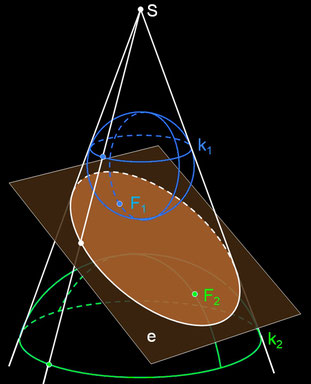
Wird ein Kreiskegel derart durch die Ebene e geschnitten, dass diese die Kegelspitze nicht enthält, dass die Ebene nicht senkrecht zur Kegelachse und nicht parallel zu einer Mantellinie des Kegels verläuft und dass alle Mantellinien nur auf einer Seite der Kegelspitze geschnitten werden, so entsteht ein Kegelschnitt in Form einer Ellipse. Dann können in den Kegel zwei Kugeln mit ihren Mittelpunkten auf der Kegelachse folgendermaßen einbeschrieben werden (s. Abbildung oben):
- Die erste Kugel wird zwischen der Kegelspitze S und der Schnittebene e so platziert, dass sie die Schnittebene in genau einem Punkt F1 und den Kegel auf einer Kreislinie k1 berührt.
- Die zweite Kugel wird unterhalb der Schnittebene so platziert, dass sie die Schnittebene in genau einem Punkt F2 und den Kegel auf einer Kreislinie k2 berührt.
Aufgrund der Symmetrie des geraden Kegels und der Kugel liegen die Kreisebenen der horizontalen Berührungskreise k1 und k2 senkrecht zur Kegelachse. Die Berührpunkte F1 und F2 sind genau die Brennpunkte des Kegelschnitts.
Beide Kugeln sind in ihrem Radius und ihrer Lage eindeutig und werden als Dandelin'sche Kugeln benannt nach dem belgischen Mathematiker Germinal Pierre Dandelin (1794-1847) [3], dessen hauptsächliches Arbeitsgebiet Kegelschnitte waren.
3D Visualisierung und Animation
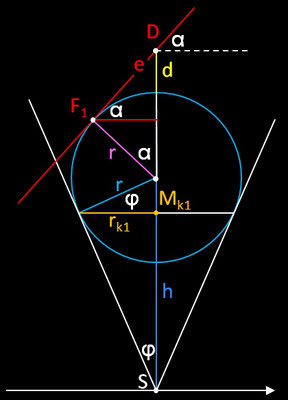
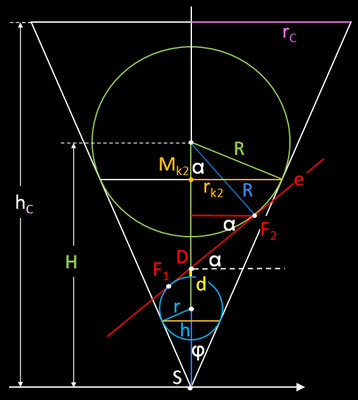
Im folgenden soll eine 3D Visualisierung und Animation der Dandelin'schen Kugeln realisiert werden. Hierbei wird ein Kegel mit dem Radius rC und der Höhe hC von einer Ebene e geschnitten. Die Höhe D und der Neigungswinkel α zur Horizontalen werden vorgegeben (animiert); die Kugeln werden dann berechnet. Für die Herleitung der erforderlichen Größen betrachte man die beiden folgenden Grafiken, die einen Längsschnitt durch den Kreiskegel mit Dandelin'schen Kugeln darstellen.
Aus
können die folgenden Größen hergeleitet werden:
• Kugelparameter:
• Brennpunkte F1 und F2 :
• Berührkreise k1 und k2:
In den folgenden Animationen ist zusätzlich die Drehachse für die Schnittebene e durch den Drehpunkt D als gelbe Strecke eingezeichnet.
Im folgenden Bild wird der Schnittwinkel α animiert. Ist α = 0, so berühren sich beide Kugeln und Schnittebene in genau einem Punkt F1≡ F2.
Bei der folgenden Animation wird die Höhe D der Schnittebene animiert. Außerdem dreht sich der Kegel um seine MIttelachse.
Iin der folgenden Grafik wird wieder der Schnittwinkel α animiert, jedoch über den Winkel hinaus, an dem die Schnittebene e parallel zu einer Mantellinie des Zylinders ist. Dieses ist bei α = π/2-φ der Fall.
Überschreitet α diesen Wert, so erscheint die zweite Kugel in der anderen Hälfte des Doppelkegels:
Im Fall α = π/2-φ (in diesem Fall ist e parallel zu einer Mantellinie) ist der Kegelschnitt eine Parabel (blaue Linie):
Im Fall α > π/2-φ ist der Kegelschnitt eine Hyperbel (blaue Linien):
Dandelin'sche Kugeln beim Zylinder

Ersetzt man im obigen Szenario den Kreiskegel durch einen Zylinder und schneidet diesen mit der Schnittebene e, so ist der entstehende Kegelschnitt ebenfalls eine Ellipse.
Eine solche Erfahrung hat man vielleicht bereits im Alltag erlebt, wenn man eine zylinderförmige Wurst (z.B. Salami) nicht im rechten Winkel zur Längsrichtung der Wurst, sondern vielmehr schräg anschneidet. Die dann entstehenden Scheiben sind nicht irgendwelche Ovale, sondern Ellipsen.
Das Erstellen einer Animation mit einem Zylinder statt eines Kreiskegels ist hinsichtlich der erforderlichen Größen etwas einfacher - siehe dazu folgende Grafik.

Im Falle des Zylinders sind beide Kugeln gleich groß.
Es gilt: Radius des Zylinders rC , Radius der Kugeln r und Radius der Berührkreise k1 und k2 sind gleich: rc = r = rk1 = rk2
Es gilt:
Die senkrechte Entfernung vom Drehpunkt D zu den Mittelpunkten der Kugeln beträgt D - d - r bzw. D + d + r.
Für die Koordinaten der Brennpunkte F1 und F2 gelten die gleichen Rechenvorschriften wie beim Szenario mit einem Kreiskegel:
Die beiden folgenden Grafiken zeigen ein Beispiel für einen Kegelschnitt am Zylinder sowie eine Animation des Schnittwinkels α zwischen Ebene e und dem Mantel.