Riemann-Summen

Längen-, Flächen- und Volumenberechnungen (bzw. allgemein Inhaltsberechnungen) waren/sind eine der Haupttriebkräfte bei der Entwicklung der modernen Analysis.

Auf dieser Seite geht es um die Inhaltsbestimmung einer Fläche A zwischen dem Funktionsgraph einer reellwertigen Funktion f mit der reellen Veränderlichen x und der x–Achse. Dazu gibt es in der modernen Analysis unterschiedliche Wege.

Im folgenden werden die sogenannten Riemann–Summen betrachtet, die in einem Grenzwertprozess zum Riemann-Integral führen.

Das vom deutschen Mathematiker Bernhard Riemann (1826 - 1866) entwickelte zugrunde liegende Konzept besteht darin, den gesuchten Flächeninhalt im Intervall [a, b] mit Hilfe leicht zu berechnender Flächeninhalte von Rechtecken anzunähern.

Im folgenden sind

f : [a, b] → ℝ eine beschränkte Funktion,
[a, b] ⊂ ℝ ein Intervall,
Z = { [x₀, x₁], [x₁, x₂], …, [x_n-1, x_n] } mit a=x₀ < x₁< … < x_n=b eine Zerlegung des Intervalls [a, b],
$[x i-$ $1, x i] ein Teilintervall von [a, b],$
$Δ$ $x i =$ $x i - x i-1 die Länge des Teilintervalls$ $[x i- 1, x i],$
$||$ $Δ x i || die Norm (Feinheit) der Zerlegung Z mit$ $|| Δ x i || = max ( {$ $Δ x i$ $| i =1, ..., n } ),$
ξ_i ∈ [x_i-1, x_i] mit i = 1, …, n zu Z gehörende Zwischenstellen.

Riemann untersuchte Summen der Form

(heute als Riemann-Summen bezeichnet). Für eine gewählte Zerlegung Z ist jeder Term in der Summe das Produkt aus dem Funktionswert an der Zwischenstelle ξ_i und der Intervalllänge und repräsentiert folglich die (vorzeichenbehaftete) Fläche des Rechtecks mit der Höhe f (ξ_i) und der Breite $Δ$ $x i$ = $x i - x i-1$ .

Die folgende Grafik zeigt dazu ein Beispiel. Die Norm der Zerlegung ist dort $||$ $Δ x i || =$ $x 5 - x 4 .$

Riemann-Summe mit allgemeiner Zerlegung von [a, b]

Die Riemann-Summe S ist die (vorzeichenbehaftete) Gesamtfläche all dieser Rechtecke.

Animation Riemann-Summe mit feiner werdender, beliebiger Zerlegung

Falls nun für eine Funktion f über dem Intervall [a, b] und für beliebige und immer feiner werdende Zerlegungen (s. Beispiel in Grafik rechts) die Riemann-Summen sich einer festen Zahl A beliebig nähern, so nennt man die Funktion integrierbar.

Hierbei müssen die einzelnen Teilintervalle nicht notwendigerweise alle gleich groß sein; auch können die Stützstellen ξ_i innerhalb eines Teilintervalls $[x i-1, x i]$ beliebig angeordnet sein.

Die Zahl A ist dann das Riemann-Integral:

Ohne Beschränkung der Allgemeinheit kann man für die Zerlegung Z eine konstante Länge $Δ$ $x für die Teilintervalle wählen, da dies die praktische Berechnung deutlich erleichtert:$

$Weiterhin ergeben sich dabei in Abhängigkeit der Wahl der Zwischenstellen$ $ξ i spezielle Riemann-Summen, die im folgenden näher betrachtet werden.$

Linke Riemann-Summe

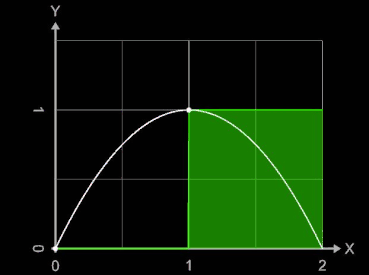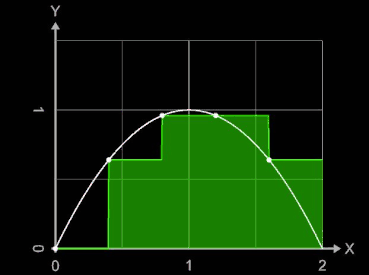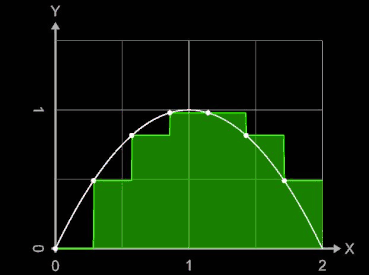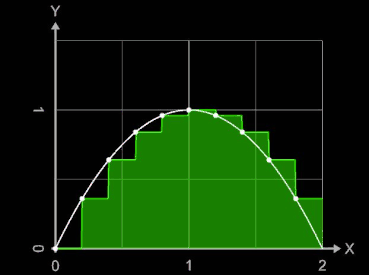
Gilt für alle Teilintervalle $[x i-$ $1, x i]$ einer Zerlegung Z, dass $ξ i =$ x_i-1 , so heißt die entsprechende Summe

Animation: Linke Riemann-Summen für f(x)=-x^2+2x mit n=2, ..., 10

linke Riemann-Summe S $L$ .

Die nebenstehende Animation zeigt für die Funktion f (x) = -x² + 2 x und das Intervall [0, 2] die entstehenden linken Riemann-Summen S $L$ für Werte von n = 2, ..., 10. Die weißen Punkte auf dem Funktionsgraph markieren die Funktionswerte der Zwischenstellen $ξ i$ .

Hierbei gilt:

Für n → ∞ ergibt sich dann als Grenzwert für die linke Riemann-Summe:

Für diese Funktion und das Intervall [0, 2] wurden für einige Werte von n die linken Riemann-Summen sowie der absolute Fehler | ∫ - S_L | berechnet:

Linke Riemannsumme - Über- und Unterschreitung der echten Fläche

Grundsätzlich gilt für T ⊆ [a, b] und die für das Teilintervall T gebildete Linke Riemann-Summe S $L$ (T) in Bezug auf die echte Fläche:

S $L$ (T) ist zu klein, falls in T gilt:
f (x) ≤ 0 und f monoton fallend
oder
f (x) ≥ 0 und f monoton steigend,
S $L$ (T) ist zu groß, falls in T gilt:
f (x) ≤ 0 und f monoton steigend
oder
f (x) ≥ 0 und f monoton fallend.

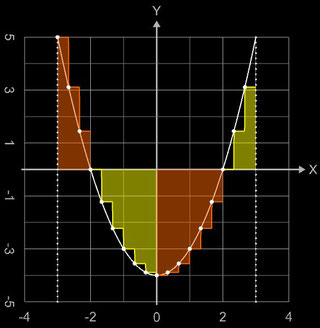
An Hand der nebenstehenden Grafik mit der Beispielfunktion f (x) = x² - 4 (für x<0 ist f monoton fallend, für x>0 monoton steigend) lassen sich die beiden obigen Aussagen nachvollziehen.

Im folgenden soll der absolute Fehler für die linke Riemann-Summe allgemein abgeschätzt werden ...

Für n = 1 gilt:

Mit der Taylor-Entwicklung für f (x) an x₀ = a mit Ordnung 1

ergibt sich:

Sei M $1$ = max ( | f '(x) | ) in [a, b], d.h. für alle x ∈ [a, b] ist | f '(x) | ≤ M $2$ .

Mit

folgt:

Für n>1 gilt somit:

wobei M $1$ das Maximum von | f '(x) | in [a, b] ist.

Rechte Riemann-Summe

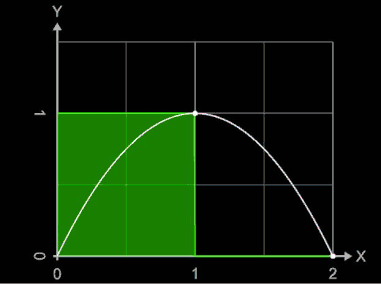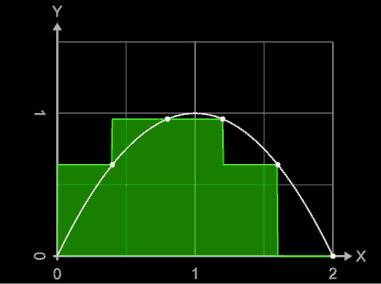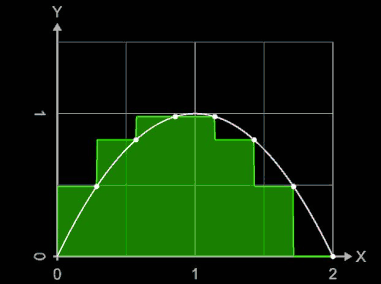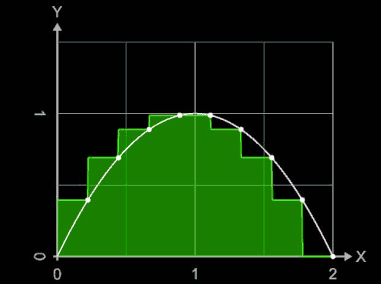
Gilt für alle Teilintervalle $[x i-$ $1, x i]$ einer Zerlegung Z, dass $ξ i =$ x_i , so heißt die entsprechende Summe

Animation: Rechte Riemann-Summen für f(x)=-x^2+2x mit n=2, ..., 10

rechte Riemann-Summe S $R$ .

Die nebenstehende Animation zeigt für die Funktion f (x) = -x² + 2 x und das Intervall [0, 2] die entstehenden rechten Riemann-Summen S $R$ für Werte von n = 2, ..., 10. Die weißen Punkte auf dem Funktionsgraph markieren die Funktionswerte der Zwischenstellen $ξ i$ .

Hierbei gilt:

Als Grenzwert für die rechte Riemann-Summe ergibt sich mit n → ∞ (vgl. oben):

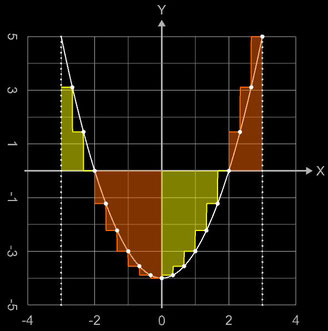
Rechte Riemannsumme - Über- und Unterschreitung der echten Fläche

Grundsätzlich gilt für T ⊆ [a, b] und die für das Teilintervall T gebildete Linke Riemann-Summe S $R$ (T) in Bezug auf die echte Fläche:

S $R$ (T) ist zu klein, falls in T gilt:
f (x) ≤ 0 und f monoton steigend
oder
f (x) ≥ 0 und f monoton fallend,
S $R$ (T) ist zu groß, falls in T gilt:
f (x) ≤ 0 und f monoton fallend
oder
f (x) ≥ 0 und f monoton steigend.

An Hand der nebenstehenden Grafik mit der Beispielfunktion f (x) = x² - 4 (für x<0 ist f monoton fallend, für x>0 monoton steigend) lassen sich die beiden obigen Aussagen nachvollziehen.

Analog zur linken Riemann-Summe ergibt sich für die Abschätzung des absoluten Fehlers der rechten Riemann-Summen:

Da die Funktion f im Intervall [0, 2] spiegelsymmetrisch zu x = 1 ist, ergibt sich für diverse Werte von n und den entstehenden Fehler die gleiche Tabelle wie bei den linken Riemann-Summen (s.o.).

Riemann'sche Mittelpunktsumme

Gilt für alle Teilintervalle $[x i-$ $1, x i]$ einer Zerlegung Z, dass $ξ i = ($ $x i-1 +$ x_i) / 2, so heißt die entsprechende Summe

Animation: Riemann-Mittelpunkt-Summen für f(x)=-x^2+2x mit n=1, ..., 10

Riemann'sche Mittelpunktsumme S $M$ .

Die nebenstehende Animation zeigt für die Funktion f (x) = -x² + 2 x und das Intervall [0, 2] die entstehenden rechten Riemann-Summen S $R$ für Werte von n = 1, ..., 10. Die weißen Punkte auf dem Funktionsgraph markieren die Funktionswerte der Zwischenstellen $ξ i$ .

Hierbei gilt:

Mit n → ∞ ergibt sich als Grenzwert für die Riemann'sche Mittelpunkt-Summe (vgl. mit oben):

Für diese Funktion und das Intervall [0, 2] wurden für einige Werte von n die Riemann-Mittelpunkt-Summen sowie der absolute Fehler | ∫ - S_M | berechnet:

Im Vergleich mit den linken und rechten Riemann-Summen (s.o.) schneidet das Mittelpunktsverfahren deutlich besser ab. Im folgenden soll der absolute Fehler für die Riemann-Mittelpunkt-Summe allgemein abgeschätzt werden ...

Für n=1 gilt:

Mit der Taylor-Entwicklung für f (x) an x₀ = (a + b) / 2 mit Ordnung 2

ergibt sich:

Sei M $2$ = max ( | f ''(x) | ) in [a, b], d.h. für alle x ∈ [a, b] ist | f ''(x) | ≤ M $2$ .

Mit

folgt:

Für n>1 gilt somit:

wobei M $2$ das Maximum von | f ''(x) | in [a, b] ist.

Riemann'sche Unter- / Obersumme

Während bei der linken und rechten Riemnannsumme für beliebige Zerlegungen die Zwischenstellen $ξ i frei gewählt werden können, hängen bei den beiden folgenden Typen von Riemann-Summen die Zwischenstellen von den Funktionswerten im jeweiligen Teilintervall ab - genauer: von Infimum bzw. Supremum der Funktionswerte im Teilintervall.$

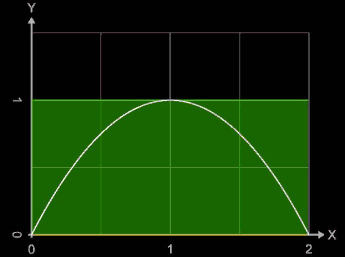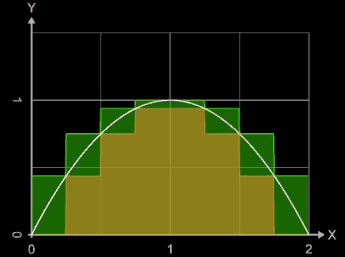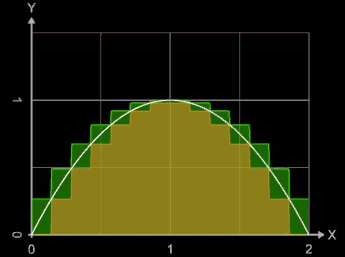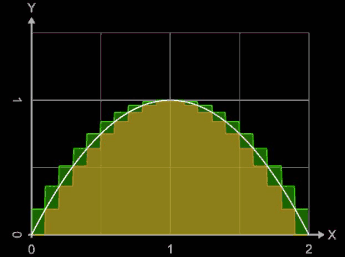
Für eine beliebige Zerlegung Z von [a, b] nennt man die Summe

Riemann (Darboux) Unter- und Obersumme

Riemann-Untersumme bezüglich der Zerlegung Z; die Summe

Riemann (Darboux) Unter- und Obersumme

nennt man Riemann-Obersumme bezüglich der Zerlegung Z.

Die Funktion wird dabei durch eine Treppenfunktion ersetzt, die auf jedem Teilintervall konstant gleich dem Supremum beziehungsweise Infimum der Funktion auf diesem Intervall ist. Die Animation zeigt für die Funktion f (x) = -x² + 2 x und das Intervall [0, 2] für Werte von n = 2, ..., 20 die entstehenden Obersummen S $O$ (grün) und Untersummen S $U$ (oliv). Für einige Werte von n wurden die Riemann-Ober- und Untersummen sowie die absoluten Fehler | ∫ - S_O | und | ∫ - S_U |berechnet:

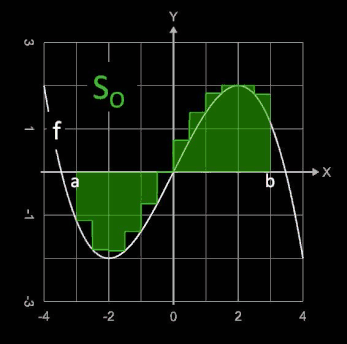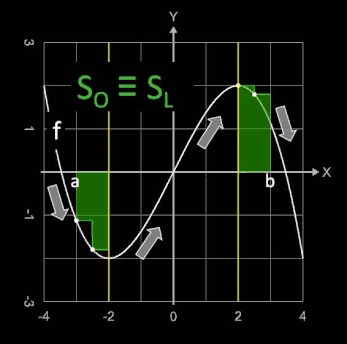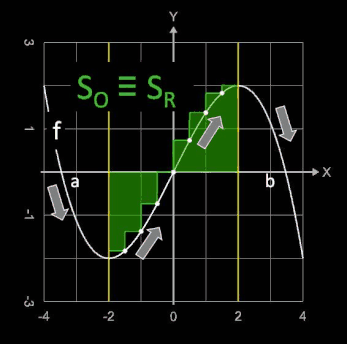
Unter- und Obersumme können für einen Funktionsabschnitt identisch mit der Linken oder Rechten Riemann-Summe sein, falls die Funktion in diesem Abschnitt entweder monoton fällt oder monoton steigt.

Grundsätzlich gelten hier für ein (Teil-)intervall T ⊆ [a, b] die folgenden Aussagen:

S $U$ ≡ S $L$ , falls f in T monoton steigt.
S $U$ ≡ S $R$ , falls f in T monoton fällt.

S $O$ ≡ S $L$ , falls f in T monoton fällt.
S $O$ ≡ S $R$ , falls f in T monoton steigt.

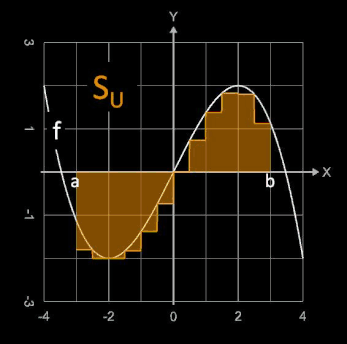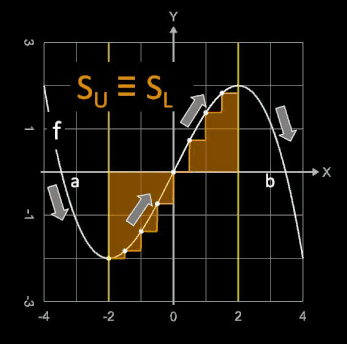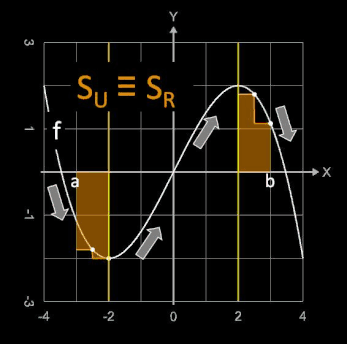
An Hand der Funktion f (x) = - 0.125 x³ + 1.5 x in den beiden folgenden Grafiken lassen sich die obigen Aussagen nachvollziehen. Die Funktion verläuft durch alle vier Quadranten und besitzt bei x = -2 und x=2 Extremwerte (s. gelbe Linie), so dass sich jeweils links und rechts davon andere Steigungsverläufe (s. Pfeile) ergeben.

Identität von Untersumme, linker und rechter Riemann-Summe

Identität von Obersumme, linker und rechter Riemann-Summe

Für alle Zerlegungen Z von [a, b] mit n Teilintervallen und beliebigen Zwischenstellen ξ_i und den zugehörigen Summen S - und somit insbesondere für S_L, S_M und S_R - gilt stets:

Weiterhin gilt grundsätzlich für alle Zerlegungen Z_k von [a, b]:

und im Falle der Gleichheit von Infimum und Supremum:

Vergleichendes Beispiel

Zum Vergleich wurden für die Funktion f (x) = - 0.45 x⁴ + 1.2 x³ + 0.5 im Intervall [-1, 3] Animationen der oben definierten Riemann-Summen S_L, S_M, S_R, S_U und S_O erstellt:

Linke Riemann-Summe f(x)=-0.45x^4+1.2x^3+0.5 mit [-1, 3]

Linke Riemann-Summe S_L

Riemann-Mittelpunkt-Summe f(x)=-0.45x^4+1.2x^3+0.5 mit [-1, 3]

Riemann-Mittelpunktsumme S_M

Rechte Riemann-Summe f(x)=-0.45x^4+1.2x^3+0.5 mit [-1, 3]

Rechte Riemann-Summe S_R

Riemann-Unter-, Obersumme f(x)=-0.45x^4+1.2x^3+0.5 mit [-1, 3]

Untere und Obere Riemannsumme S_U, S_O

Im Intervall [-1, 3] ist für -1 ≤ x ≤ 2 f monoton steigend, für 2 ≤ x ≤ 3 ist f monoton fallend, und es gibt Bereiche, für die f (x) < 0 gilt, d.h. der Funktionsgraph liegt unterhalb der x-Achse und der entsprechende Flächenanteil ist somit negativ. Die exakte vorzeichenbehaftete Fläche A beträgt

Für n = 100, 1000, 10000 wurden die Werte der Riemann-Summen berechnet:

Das beste Konvergenzverhalten zeigt die Mittelpunkt-Summe. Allerdings gibt es zur numerischen Berechnung des Integrals weitaus leistungsfähigere Verfahren, wie z.B. die Summierte Simpson Regel (s. Numerische Integration).

Um z.B. die Genauigkeit der Mittelpunkt-Summe mit n = 1000 (ca. vier Nachkommastellen) zu erhalten, benötigt man mit diesem Verfahren nur 46 Iterationsschritte, im Falle von n = 10000 und sechs Nachkommastellen nur 144 Iterationsschritte!

[1] https://de.wikipedia.org/wiki/Bernhard_Riemann