Nullstellen - Grundlagen
Nullstellen von Funktionen haben im Kontext der Funktion unterschiedlichste Bedeutungen. Beispiele hierfür sind der Aufschlagpunkt einer Wurfparabel, Stellen, an denen die Steigung der Funktion Null ist, die Temperatur, bei der Wasser gefriert, etc.
Im folgenden werden nur Funktionen betrachtet, die auf dem rellen Zahlenkörper |R definiert sind und insbesondere deren reelle Nullstellen.
Geometrisch gesehen ist die Nullstelle einer Funktion f die Stelle auf der x-Achse, an denen der Funktionsgraph die x-Achse schneidet oder berührt.
Algebraisch sind die Nullstellen einer Funktion f die Lösungen der (nichtlinearen) Gleichung f (x) = 0.
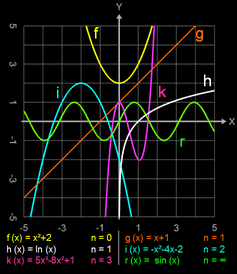
Funktionen können keine, eine, mehrere und sogar unendlich viele Nullstellen besitzen (s. Grafik rechts).
Mehrfache Nullstelle
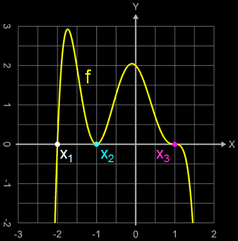
Eine Funktion kann mehrfache Nullstellen besitzen.
So hat z.B. die Funktion f (x) = – x6 – x5 + 4x4 + 2x3 – 5x2 – x + 2 in der Grafik rechts bei x1 = -2 eine einfache, bei x2 = -1 eine doppelte und bei x3 = 1 eine dreifache Nullstelle.
Es gilt:
- Eine stetige und an der Stelle x0 differenzierbare Funktion f hat bei x0 eine mehrfache Nullstelle, wenn dort die Steigung 0 ist, wenn also f ' (x0) = 0 gilt.
Ist f öfter differenzierbar, lässt sich diese Bedingung mehrfach wiederholen und es gilt für eine natürliche Zahl k:
- Eine (mindestens) k-mal differenzierbare Funktion hat in x0 eine k-fache Nullstelle, wenn f selbst und die ersten k-1 Ableitungen von f an der Stelle x0 den Wert 0 annehmen und die k-te Ableitung ungleich 0 ist: f (x0) = 0, f '(x) = 0, f ''(x) = 0, …, f (k-1)(x0) = 0, f (k)(x0) ≠ 0
Für die obige
6-mal differenzierbare Funktion gilt:
f (x) = – x6 – x5 + 4x4 + 2x3 – 5x2 – x + 2 f (-2) = 0 f (-1) = 0 f (1) = 0
f ' (x) = – 6x5 – 5x4 + 16x3 + 6x2 – 10x – 1 f '(-2) = 27≠ 0 f '(-1) = 0 f '(1) = 0
f ''(x) = – 30x4 – 20x3 + 48x2 + 12x – 10 f ''(-1) = 16≠ 0 f ''(1) = 0
f '''(x) = – 120x3 – 60x2 + 96x + 12 f '''(1) = -72 ≠ 0
Nullstellen von Polynomen
Für ein Polynom vom Grad (höchste vorkommende Potenz) n, d.h. für eine Funktion f der Struktur
wobei a0, …, an reelle und die Exponenten natürliche Zahlen sind, gelten folgende Aussagen:
- Ein Polynom vom Grad n kann höchstens eine n-fache Nullstelle besitzen.
- Ein Polynom vom Grad n kann höchstens n Nullstellen besitzen.
- Ist der Grad n ungerade, so hat hat das Polynom mindestens eine Nullstelle.
- Ist der Grad n gerade, so kann das Polynom keine Nullstelle besitzen.
Polynomdivision
Für ein Polynom vom Grad n gilt folgender Satz:
- Hat ein Polynom vom Grad n an der Stelle x0 eine Nullstelle, dann lässt sich ein Linearfaktor (x - x0) abspalten, so dass gilt:
f (x) = (x - x0) • g (x)
wobei das Polynom g dann nur noch den Grad n-1 besitzt.
Die letzte Aussage ist insbesondere für Polynome mit einem Grad größer oder gleich 3 für die Bestimmung der Nullstellen hilfreich, denn
d.h. es ist nur noch die Gleichung g (x) = 0 zu untersuchen. Im Falle einer kubischen Funktion f ist g quadratisch, so dass nur noch eine einfache quadratische Gleichung zu lösen ist.
Das Polynom g (sog. Restpolynom) lässt sich mittels einer Polynomdivision ermitteln:
f (x) : (x - x0) = g (x).
Hierzu ein Beispiel:
f (x) = x³ + x² - 17 x + 15, bestimme die Nullstellen
- f (x) = 0
- rate Lösung: x0 = 1 f (1) = ... = 0 o.k.
- Polynomdivision:
(x³ + x² - 17 x + 15) : (x - 1) = x² + 2 x - 15
- (x³ - x²)
2 x² - 17 x
- (2x² - 2 x)
15 x + 15
- (15 x +15)
0
- Restpolynom zu Null setzen und lösen:
x² + 2 x - 15 = 0
...
x1 = 3 x2 = - 5
Das Verfahren der Polynomdivision entspricht im Wesentlichem dem Verfahren des schriftlichen Dividierens zweier Zahlen, wie z.B.
Für meine Schüler(innen) hatte ich einst ein kleines Erklärvideo erstellt, das die einzelnen Schritte bei der Polynomdivision zeigt:
Für Polynome mit einem Grad n > 3 lässt sich das Verfahren wiederholt anwenden.
Beispielsweise ergibt sich für die Bestimmung der Nullstellen von f (x) = x4 - x3 – 7x2 + x + 6 das folgende Schema:
f (x) =
x4 - x3 - 7x2 + x + 6 = 0
Rate Lösung: x0 = 1 f (1) = ... = 0 o.k.
Polynomdivision ergibt: x³ - 7 x - 6
x³ - 7 x - 6 = 0
Rate Lösung: x1 = - 1
Polynomdivision ergibt: x² - x - 6
x² - x - 6 = 0
x2 = - 2 x3 = 3
Die Funktion f kann somit vollständig in Linearfaktoren zerlegt werden, so dass man sofort die Nullstellen und deren Vielfalt ablesen kann:
f (x) = (x + 2) (x + 1) (x - 1) (x - 3)
Das Auffinden ganzzahliger Nullstellen für die Polynomdivision kann sehr mühselig sein. Die Auswahl solcher Nullstellen wird durch folgenden Satz eingeschränkt:
- Sind bei einem Polynom die Koeffizienten a0, …, an alle ganzzahlig, so ist jede ganzzahlige Nullstelle ein Teiler von a0 .
Für die letzte Beispielfunktion sind z.B. {-3, -2, -1, 1, 2, 3} die Teiler von a0; bis auf die Werte 2 und -3 lassen sich diese Teiler für die Polynomdivision verwenden.
Der zuvor genannte Satz bedeutet hingegen nicht, dass die Nullstellen von f auch ganzzahlig sind. So hat z.B. f (x) = x² - 2 nur ganzzahlige Koeffizienten,
ihre Nullstellen sind aber irrational mit x0 = - √2
und x1 =
√2. Auch die Funktion f (x) = x³ + 2x - 1 hat nur ganzzahlige Koeffizienten, als reelle Lösung aber eine Irrationalzahl.
Ist die Funktion f normiert, d.h. vor der höchsten Potenz von x kommt kein Faktor (genauer: nur 1 als Faktor) vor, so gibt es, falls alle Koeffizienten ganzzahlig sind, auch keine echten Brüche als Nullstellen. Alle Nullstellen sind dann ganzzahlig oder irrational.
Beispielsweise ist die Funktion f (x) = x³ - 5 x² - 3 x + 15 normiert und enthält nur ganzzahlige Koeffizienten. Die Nullstellen sind x0 = 5, x0 = - √3 , x2 = √3 .
Die Darstellung in Linearfaktoren ergibt: f (x) = (x +
√3) (x -
√3) (x –
5).
Lässt sich, wie z.B. bei der Funktion f (x) = x³ - 2x + 2 keine ganzzahlige Nullstelle finden, um das Polynom zu reduzieren, so kann man für diese Funktion auf die Cardanischen Formeln [1] zum Lösen einer kubischen Gleichung zurückgreifen - ein zugegebenermaßen etwas mühseliger Weg:
Für Polynome 4. Grades existieren für f (x) = 0 zwar geschlossene Lösungen, jedoch sind diese recht unübersichtlich [2].
Niels Henrik Abel konnte im Jahr 1824 beweisen, dass für den Grad 5 und größer keine algebraische Lösung [3] (d.h. eine Lösung mit den Operationen Addition, Subtraktion, Multiplikation, Division, Potenz mit ganzzahligem Exponenten n und n-te Wurzel) existiert [4].
Nullstellen bestimmen mit numerischen Verfahren
Für beliebige stetige Funktionen f lässt sich die Gleichung f (x) = 0 mit Hilfe von numerischen Verfahren lösen.
Bei diesen Verfahren kann man unterscheiden zwischen Vefahren, die auf einer Intervallschachtelung basieren, wie z.B. Bi-Sektion [5] oder Regula Falsi 6] und Iterative Verfahren.
Letztere sind Gegenstand auf meiner Webseite Nullstellen, wobei einige Grundlagen und wichtige Größen in Iterative Verfahren zur Nullstellenbestimmung erklärt werden. Weiterhin werden diverse Verfahren vorgestellt, von denen einige (Sekanten-, Newton-, Schröder-, Tiruneh-, Halley-, und Ostrowski-Verfahren) näher betrachtet werden.
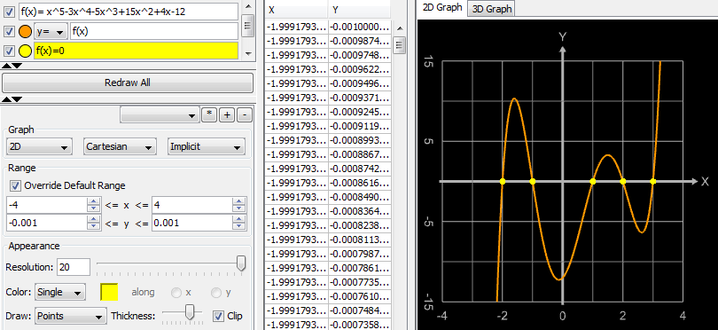
Nullstellen bestimmen mit Graphing Calculator 3D
Da der Graphing Calculator 3D implizite Gleichungen lösen kann, lassen sich mittels f (x) = 0 auch die Nullstellen von f bestimmen. Als Beispiel diene die Funktion f (x) = mit den Nullstellen {-2, -1, 1, 2, 3}:
GC3D liefert bei einer Plot-Auflösung von 100 für den x-Bereich [-4, 4] die folgenden Lösungen:
{-1.9999667…, -0.9999980…, 1.0000157…, 1.9999891…, 2.9999787…}.
Die Genauigkeit lässt sich noch verbessern, indem man einen engen x-Bereich um die Nullstellen legt und die Plot-Auflösung entsprechend hoch wählt.
Nachteilig ist, dass der Graphing Calculator 3D in einigen Fällen trotz hoher Auflösung nicht unbedingt sämtliche Lösungen findet und dass man die Lösungen aus der Wertetabelle für den Plot entnehmen muss und diese nicht in Variablen zur Verfügung stehen, mit denen man direkt weitere Berechnngen durchführen kann. Hierfür greift man besser auf numerische Verfahren (s.o.) zurück.
Quellenverweise
[1] https://de.wikipedia.org/wiki/Cardanische_Formeln
[2] https://de.wikipedia.org/wiki/Quartische_Gleichung
[3] https://en.wikipedia.org/wiki/Algebraic_solution
[4] https://en.wikipedia.org/wiki/Abel%E2%80%93Ruffini_theorem
[5] https://de.wikipedia.org/wiki/Bisektion
[6] https://de.wikipedia.org/wiki/Regula_falsi