Ein-Schritt-Verfahren (one-step methods)

Die Anwendung der im folgenden betrachteten Verfahren für eine Vielzahl komplexer Funktionen finden Sie unter Basins of Attraction.

Das Newton-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ beruht auf der Iterationsvorschrift

Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Newton-Verfahren für reelle Funktionen.

Im Falle einer mehrfachen Nullstelle konvergiert das Newton-Verfahren nur noch linear. Besitzt die Funktion eine a-fache Nullstelle (a ∈ |N, a ≥ 2), so liefert das modifizierte Verfahren

aber wieder lokal quadratische Konvergenz. Sehr schön kann man das am folgendem Beispiel erkennen.

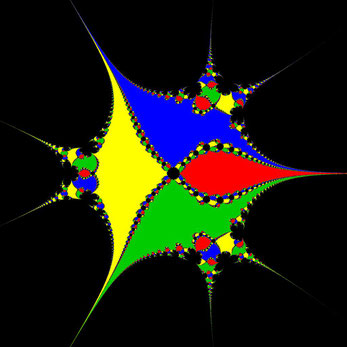
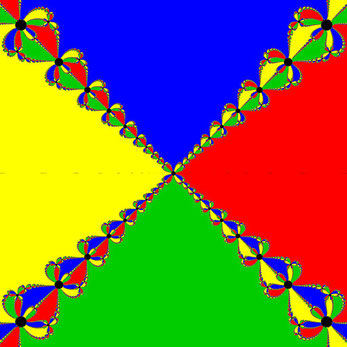
Die Funktion f (z) = (z² - 1) ² = 0 besitzt die beiden doppelten Nullstellen ζ_1,2 = -1,  ζ_3,4 = 1. Sowohl das Newton- als auch das modifizierte Newton-Verfahren (a = 2) liefern für B = [-4, 4] × [-4, 4] ⊆ ℂ die gleichen Basins of Attraction (s. erstes Bild in folgender Galerie). Stellt man jedoch die Konvergenzgeschwindigkeit für diesen Bereich B mit Hilfe einer Regenbogen-Farbpalette dar (s. dazu Basins of Attraction - Algorithmen), so zeigt sich an Hand der vorherrschenden Blautöne, dass das Verfahren mit a = 1 deutlich langsamer konvergiert (s. mittleres Bild in Galerie) als das Vefahren mit a = 2 und vorherrschenden Rot-/Gelb-Tönen (s. letztes Bild in Galerie).

Die Iterationsvorschrift für das Halley-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ lautet

Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Halley-Verfahren für reelle Funktionen.

Das Schröder-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ beruht auf der Iterationsvorschrift

Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Schröder-Verfahren für reelle Funktionen.

Das hier betrachtete Householder-Verfahren [1], [2] für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ beruht auf der Iterationsvorschrift

Es hat die Konvergenzordnung q = 3 und den Effizienzindex CE = 1.442.

Quellenverweise

[1]   https://mathworld.wolfram.com/HouseholdersMethod.html

[2]   https://de.wikipedia.org/wiki/Householder-Verfahren

Die Iterationsvorschrift für das Basto-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ lautet [1]:

Das Verfahren besitzt die Konvergenzordnung q = 3 bei einem Effizienzindex CE = 1.442.

Quellenverweise

[1]     M. Basto et al., A new iterative method to compute nonlinear equations (2006),
         Applied Mathematics and Computation 173 (2006), (468–483)

Das von Whittaker entwickelte Verfahren mit konvexer Beschleunigung (engl. convex acceleration) beruht auf dem Newton-Verfahren und besitzt die Konvergenzordnung q = 2 und den Effizienzindex CE = 1.26.

Angewandt auf komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ lautet die Iterationsvorschrift:

Quellenverweise

[1]   J. M. Ortega, W. C. Rheinboldt, Iterative solution of nonlinear equations in several variables (1970),
       Monographs Textbooks Comput. Sci. Appl. Math., Academic Press, New York, 1970, S.181 ff

Whittaker entwickelte sein Verfahren mit konvexer Beschleunigung  (s.o. Whittaker I - Verfahren) weiter zu einem Verfahren mit doppelt konvexer Beschleunigung (engl. double convex acceleration) [1]. Das neue Verfahren hat die höhere Konvergenzordnung q = 3 bei einem Effizienzindex CE = 1.442.

Die neue Iterationsvorschrift, angewandt auf komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ, lautet:

Quellenverweise

[1]   M. Heydari, G.B. Loghmani (2014) Third-Order and Fourth-Order Iterative Methods Free from Second
       Derivative for Finding Multiple Roots of Nonlinear Equations, CJMS 3(1)(2014), (67-85)

[2]   B. Neta, C. Chun, (2013) On a family of Laguerre methods to find multiple roots of nonlinear equations,
       Applied Mathematics and Computation 219 (2013) 10987–11004

http://dx.doi.org/10.1016/j.amc.2013.05.002

Das Euler-Chebyshev-Verfahren beruht auf der Iterationsvorschrift

und ist insbesondere für mehrfache Nullstellen, d.h. Nullstellen der Vielfachheit m geeignet, lässt sich aber auch für einfache Nullstellen einsetzen. Es handelt sich um ein Verfahren der Konvergenzordnung q = 3 bei einem Effizienzindex von CE = 1.442.

Quellenverweise

[1]   M. A. Hernandez, An acceleration procedure of the Whittaker method by means of convexity (1990),
       Zb. Rad. Prirod.-Mat. Fak. Ser. Mat. 20 (1990), 27–38

Die Verfasser konstruieren in [1] ein neues Verfahren basierend auf einer geometrischen Herangehensweise, ähnlich wie der mit der Tangente beim Newton-Verfahren und einer Hyperbel beim Halley-Verfahren (s. die dortigen Animationen). Hierbei nehmen sie aber den Krümmungskreis zur Hilfe, der im Punkt (x_n | y_n) die gleiche Tangente wie die Funktion f  besitzt. SIe leiten die folgende  Iterationsvorschrift für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ her:

Das Verfahren besitzt die Konvergenzordnung q = 3, der Effizienzindex beträgt CE = 1.442.

Es entspricht dem Householder-Verfahren (s.o.).

Quellenverweise

[1]   C. Chun · Y. I. Kim, Several New Third-Order Iterative Methods for Solving Nonlinear Equations (2010),
       Acta Appl. Math. (2010) 109: 1053–1063, DOI 10.1007/s10440-008-9359-3

Für ein komplexes Polynom p (z) vom Grad n ≥ 2 lautet die Iterationsvorschrift des Laguerre-Verfahrens:

mit

wobei das Vorzeichen der Wurzel so gewählt wird, dass der absolute Betrag der Nenner maximal ist.

Eine Herleitung des Verfahrens an Hand eines allgemeinen Polynoms findet man bei [2], [3].

In verschiedenen Publikationen und insbesondere auch in [4] von 2014 erklären die Verfasser, dass "das Laguerre-Verfahren eines der am wenigsten verstandenen Methoden der Numerischen Analysis ist".

Definitiv bekannt sind folgende Eigenschaften des Laguerre-Verfahrens:

• Im Falle einer einfachen Nullstelle besteht kubische Konvergenz, q = 3.
  
• Im Falle einer mehrfachen Nullstelle weist das Verfahren lineare Konvergenz auf.
• Für ein reelles Polynom mit reellen Nullstellen konvergiert das Verfahren für jeden (!) Startwert z₀ ∈ |R gegen eine Nullstelle. Aufgrund der Quadratwurzel im Nenner (s.o.) kann das Verfahren trotz eines reellen Startwertes zu einer komplexen Lösung konvergieren.

Bělik et al. untersuchten in [4] das Verhalten des Verfahrens beim Lösen von  zⁿ – 1 = 0  und fanden interessante Ergebnisse für die Basins of Attraction (s. dazu  z^n-1=0 Laguerre-Verfahren).

Außer für Polynome kann das Verfahren auch für allgemeine Funktionen verwendet werden. Für den "Grad" n können beliebige Werte verwendet werden. Jedoch ergeben sich laut [5] üblicherweise die besten Resultate für n = 2. In diesem Fall entspricht das Verfahren der Halley Irrational Formula [6]. Als Beispiel dazu zeigt die folgende Galerie für  exp (z) - 1 = 0   und den Bereich B = [-10, 20] x [-15, 15] die mit dem Laguerre-Verfahren berechneten Basins of Attraction für verschiedene Werte von n.

Weitere Anwendungen des Laguerre-Verfahrens auf Exponential- und trigonometrische Funktionen finden Sie unter Numerik/Basins of Attraction.

Quellenverweise

[1]   M. Laguerre, Sur une méthode pour obtenir par approximation les racines d’une équation

       algébrique qui a toutes ses racines réelles, Nouvelles annales de mathématiques 2e série, tome 19

       (1880), S. 161-171

       http://www.numdam.org/item?id=NAM_1880_2_19__161_1

[2]   https://en.wikipedia.org/wiki/Laguerre%27s_method

[3]   https://mathworld.wolfram.com/LaguerresMethod.html

[4]   P. Bělik, H. Kang, A. Walsh, E. Winegar (2014)
       Analysis of Laguerre's method applied to find the roots of unity, arXiv:1405.0780

[5]   A, N. Amin (2015) Unification of Well-known Numeric Methods for Solving Nonlinear Equations,
       American Journal of Numerical Analysis, 2015, Vol. 3, No. 3, 65 - 76,
       http://pubs.sciepub.com/ajna/3/3/2/

[6]   https://mathworld.wolfram.com/HalleysIrrationalFormula.html 

Das Sekantenverfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ beruht auf der Iterationsvorschrift

Das Verfahren benötigt außer dem Startwert z₀ ϵ B noch einen zweiten Startwert z₁ ϵ B.

Für weitere Details, Herleitung, Konvergenzordnung q und Effizienzindex CE siehe Sekantenverfahren für reelle Funktionen. Die Anwendung des Verfahrens für einige komplexe Funktionen finden Sie unter Basins of Attraction.

Die Verfasser konstruieren in [1] ein "modifiziertes Sekanten-Verfahren", wobei sie eine Sekante und Parabel kombinieren. Mit Hilfe des Parameters α entsteht eine Familie von Verfahren ähnlich dem Sekanten-Verfahren.

Für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ lautet die Iterationsvorschrift:

Hierbei ist das Vorzeichen der Wurzel so zu wählen, dass der Nenner möglichst groß ist.

Mit α → 0 ergibt sich das "normale" Sekanten-Verfahren.

Das Verfahren zeigt super-lineare Konvergenz, d.h. es besitzt die Konvergenzordnung q = 1.618.

Quellenverweise

[1]   V. Kanwar, J.R. Sharma, A new family of Secant-like method with super-linear convergence (2005),
       Applied Mathematics and Computation 171 (2005) S. 104–107

Angewandt auf komplexe Funktionen  f : D → ℂ  mit  D ⊆ ℂ lautet die Iterationsvorschrift für das Thukral-Verfahren

Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Thukral-Verfahren für reelle Funktionen.

Die Iterationsvorschrift für das Tiruneh-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ lautet

Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Tiruneh-Verfahren für reelle Funktionen.

Die Iterationsvorschrift für das Steffensen-Verfahren für komplexe Funktionen f : D → ℂ  mit  D ⊆ ℂ ergibt sich, wenn man beim Newton-Verfahren die Ableitung durch den (rechtsseitigen) Differenzenquotienten ersetzt:

Für weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Steffensen-Verfahren für reelle Funktionen.

Eine Variante des Steffensen-Verfahrens hat einen zusätzlichen Parameter β und besitzt die folgende Iterationsvorschrift [1]:

Es ist bekannt, dass dieses Verfahren für jeden von Null verschiedenen Wert des Parameters β eine quadratische Konvergenz hat, jedoch spielt der Parameter β eine wichtige Rolle in Bezug auf die Stabilität der Methode.

Zum einen können bei dieser Variante des Steffensen-Verfahrens die Basins of Attraction durch Wahl eines kleinen Wertes für β stark verbessert werden. Die folgenden Grafiken zeigen dies am Beispiel für z³ - 1 = 0 mit einem Bereich B = [-10, 10] x [-10, 10] und unterschiedlichen Werten für β.

Zum anderen lässt sich zeigen (s. [1], S. 5) und eyperimentell beobachten, dass für sehr kleine Werte für β die berechneten Basins of Attraction denen des Newton-Verfahrens ähnlich werden, wie in der folgenden Galerie am Beispiel für z³ - 1 = 0 und einem Bereich B = [-2, 2] x [-2, 2] dargestellt. Das linke Bild zeigt das Ergebnis mit dem Newton-Verfahren; bei der Animation im rechten Bild durchläuft der Parameter β die Werte von 1, 0.9, 0.8, ..., 0.1, 0.01, 0.001, ..., 0.000001. 

Mit kleinen Werten für β ergibt sich ein weiterer Effekt: die Rechenzeiten werden auf Grund der kleineren Bereiche, in denen das Verfahren nicht konvergiert, drastisch verkürzt. So erfolgt z.B. die Berechnung für
z^4 - 1 = 0 und B = [-10, 10] x [-10, 10] für β = 0.000001 ca. 6-mal schneller als für β = 0.01.

Quellenverweise

[1]   A. Cordero, F. Soleymani, J. R. Torregrosa, S. Shateyi (2014) Basins of Attraction for Various
       Steffensen-Type Methods, Journal of Applied Mathematics, Volume 2014, Article ID 539707,
       http://dx.doi.org/10.1155/2014/539707

Das ursprünglich von Ridders vorgestellte Verfahren zur Nullstellenbestimmung reeller Funktionen beruht auf der Basis der regula falsi  und benötigt 3 Punkte [1], [3]:

Hierbei gilt:

• x_i ∈ [x_i-2 , x_i-1]
• die Werte von f (x_i-2) und f (x_i-1) müssen unterschiedliche Vorzeichen haben. 

Liegen die drei Punkte eng bei einander, so kann die Iterationsvorschrift folgendermaßen umgeschrieben werden [2]:

bzw. für den komplexen Fall

Quellenverweise

[1]   C.J.F. Ridders, A New Algorithm for Computing a Single Root of a Real Continuous Function (1979),
       IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS, Vol. CAS-26, NO. 11, NOVEMBER 1979

[2]   Amin Najafi Amin, Unification of Well-known Numeric Methods for Solving Nonlinear Equations (2015)
       American Journal of Numerical Analysis, 2015, Vol. 3, No. 3, S. 65-76, DOI:10.12691/ajna-3-3-2

[3]   AM225: One-dimensional root finding methods, https://courses.seas.harvard.edu

In [1] leiten die Verfasser vier Verfahren zur Nullstellenbestimmung reeller Funktionen her. Ihr Ansatz beruht hierbei darauf, die Funktion in der Umgebung der Nullstelle weder durch eine Sekante wie beim Sekantenverfahren, durch eine Tangente wie beim Newton-Verfahren noch durch eine Hyperbel wie beim Halley-Verfahren zu approximieren, sondern vielmehr eine quadratische Spline-Interpolation auf zwei aufeinanderfolgende Werte x_i und x_i-1 der Iterationsfolge anzuwenden, um das nächstfolgende Glied x_i+1 zu bestimmen. Die Iterationsvorschriften übertragen ins Komplexe lauten:

      •  Verfahren I

      •  Verfahren II

      •  Verfahren III

      •  Verfahren IV

Für die ersten beiden Verfahren beträgt die Konvergenzordnung q = 3 und der Effizienzindex CE = 1.442.

Die beiden letzten Verfahren besitzen die Konvergenzordnung q = 4, erfordern jedoch die Berechnung der dritten Ableitung f ''' der Funktion f, wodurch sich ein niedrigerer Effizienzindex von CE = √2.  ergibt.

Quellenverweise

[1]   R. Saeed and K. M. Aziz, Iterative methods for solving nonlinear equations by using quadratic
       spline function (2013), Math. Sci. Lett. 2, No.1, (2013), S. 37-43

Auf der Basis einer Taylor-Reihenentwicklung und entsprechenden Abschätzungen entwickelt der Verfasser in [1] das folgende Iterationsverfahren:

Es hat die Konvergenzordnung q = 4  bei einem Effizienzindex von CE = √2 ≈ 1.4142.

Quellenverweise

[1]   M. M. Hosseini, A Note on One-step Iteration Methods for Solving Nonlinear Equations (2009)
       World Applied Sciences Journal 7 (Special Issue for Applied Math): 90-95, 2009

In [1] leiten die Verfasser Verfahren zur Lösung nichtlinearer Gleichungen auf Basis der Homotopie-Störungsmethode her. Die Störungstheorie findet vor allem Anwendung in der Physik. Hierbei wird ein kompliziertes Problem zunächst so lange durch Ignorieren kleiner Einflüsse idealisiert, bis es auf ein Problem mit bekannter Lösung reduziert ist. Danach werden die zuvor ignorierten Einflüsse als kleine Störungen (Störgröße) wieder dem System hinzugefügt und eine Näherungslösung berechnet. Die Homotopie ist in der Topologie die stetige Deformation eines topologischen Objekts in ein anderes topologisches Objekt (z.B. Morphing).

Ende der Neunziger koppelte He Störungsmethoden und Homotopie [2]. Das Verfahren wurde von He weiterentwickelt und auf nichtlineare Probleme angewandt und kann verschiedene Arten nichtlinearer Gleichungen lösen.

Golbabai und Javidi entwickelten die folgenden beiden Algorithmen:

      •  Algorithmus 1

      •  Algorithmus 2

Beide haben die Konvergenzordnung q = 3 bei einem Effizienzindex von CE = 1.442.

Quellenverweise

[1]   A. Golbabai, M. Javidi (2007) A third-order Newton type method for nonlinear equations
       based on modified homotopy pertubation method, Applied Mathematics and Computation 191 (2007),
       S. 199–205, doi:10.1016/j.amc.2007.02.079

[2]   J.-H. He (1999) Homotopy pertubation technique, Comput. Methods Appl. Mech. Engrg. 178 (1999),
       S. 257-262, https://doi.org/10.1016/S0045-7825(99)00018-3

Eine Familie modifizierter Schröder-Verfahren stellen die Verfasser in [1] mit p ∈ ℝ auf:

Für p = 0 ergibt sich das "normale" Schröder-Verfahren.

Das modifizierte Verfahren hat ebenfalls quadratische Konvergenz; setzt man p = f '' (x_n) / 2 f ' (x_n), so ergibt sich sogar kubische Konvergenz. Das jeweilige Konvergenzverhalten gilt auch für mehrfache Nullstellen.

Quellenverweise

[1]   R. Behl, V. Kanwar, K. K. Sharma (2012) Another Simple Way of Deriving Several Iterative

       Functions to Solve Nonlinear Equations, Journal of Applied Mathematics, Volume 2012,
       Article ID 294086, https://doi.org/10.1155/2012/294086