Funktionsgraph aus 3D-Objekten
Für Animationen mit dem Graphing Calculator 3D im Bereich der Physik (u.a. für eine Kettenlinie) wird die Darstellung des Funktionsgraphens einer Funktion y = f (x) durch sich berührende Kugeln benötigt.
Nach Herleitung des Algorithmus für Kugeln wird im weiteren Verlauf der Seite die Darstellung des Funktionsgraphens durch andere 3D-Objekte oder 2D-Objekte betrachtet.
Funktionsgraph aus Kugeln
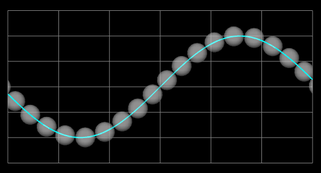
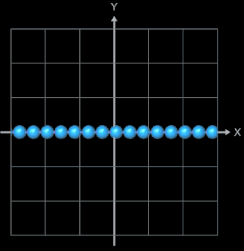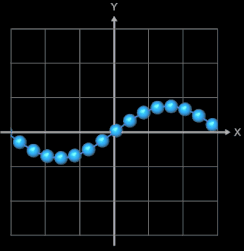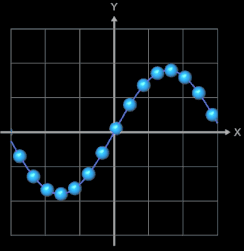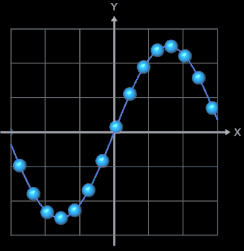
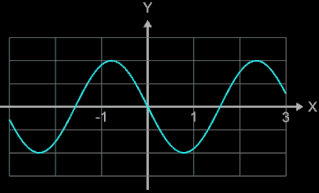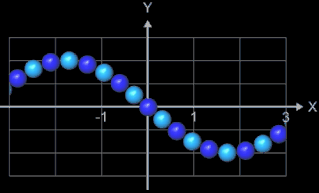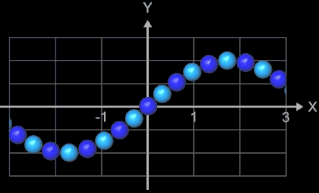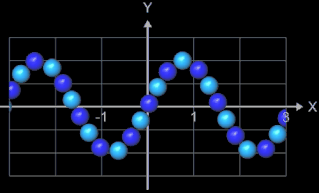
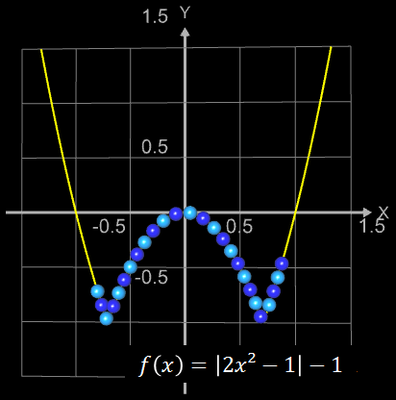
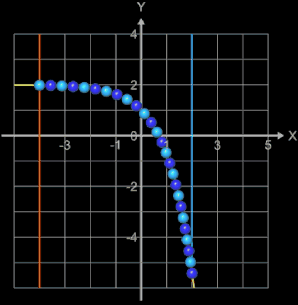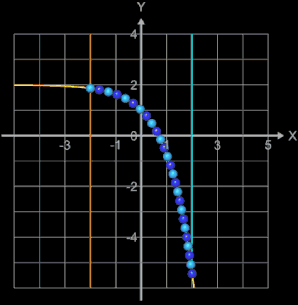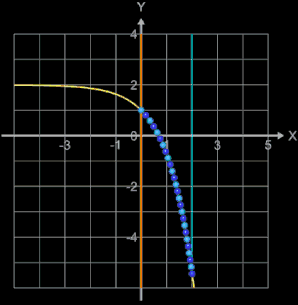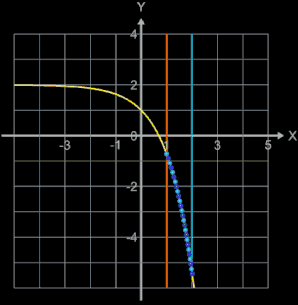
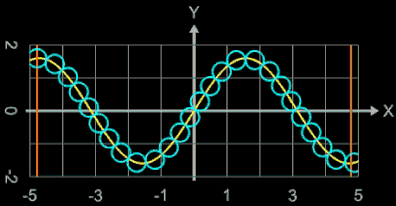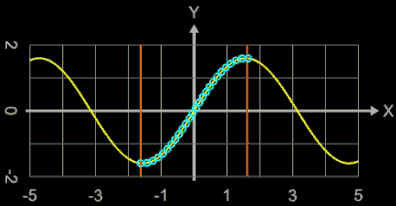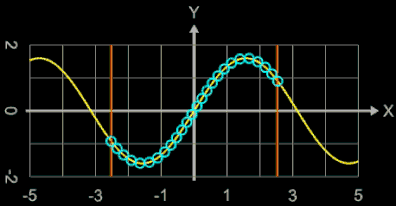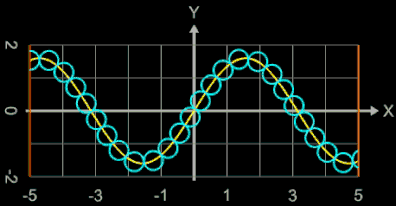
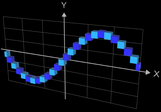
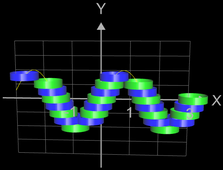
Der Graph bildet quasi eine "Perlenkette", wobei die Kugeln (diese werden als Parameterfläche erzeugt) längs des Funktionsgraphs von f (blau im nebenstehenden "Röntgenbild") aufgereiht sind.
Für die Kugeln gilt:
- alle Kugelmittelpunkte liegen auf dem Graph,
- je zwei benachbarte Kugeln berühren sich in genau einem Punkt.
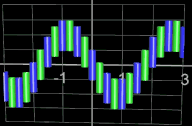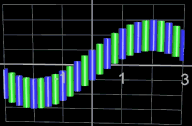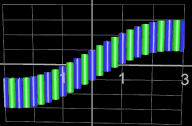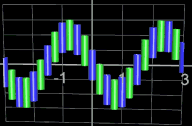
Wählt man als x-Abstand der Kugelmittelpunkte den Wert von 2 • r, so berühren sich die Kugel nur für den Fall einer horizontalen Linie. Je nach Verlauf des Funktionsgraphen entstehen dann natürlich Lücken, wie man dies in der folgenden linken Animation am Beispiel der Funktion f (x) = t • sin (x) gut sehen kann; dabei durchläuft der Parameter t die Werte von 0 bis 2.5.
Damit die Kugeln "zusammenhängend" erscheinen, muss die Position einer jeden Kugel folglich "individuell" bestimmt werden; sie hängt jeweils von der Position ihrer Vorgängerkugel ab. Dazu betrachte man die obere rechte Grafik.
Der Mittelpunkt der (i-1)-ten Kugel liege auf dem Funktionsgraphen von f. Für die Position des Mittelpunktes
(pi
| f (pi
+ ∆ i) der folgenden i-ten Kugel muss ein geeignetes ∆ i bestimmt werden. Hierfür gilt nach Pythagoras
Diese Gleichung kann für ∆ i und eine beliebige Funktion f nur numerisch gelöst werden.
Hierzu wurde zunächst das Newton- sowie das Halley-Verfahren herangezogen. Wie zu erwarten war, konnte für verschiedene Funktionen eine Vielzahl an korrekten Werten für ∆ i bestimmt werden, jedoch versagten die Verfahren oftmals in Bereichen, an denen die Funktionen Extremwerte aufwiesen (vgl. Numerik / Nullstellen). Mithin ist diese Vorgehensweise nicht zielführend, da ja die Position einer jeden Kugel von der Position ihrer Vorgängerin abhängt.
Als Lösung im Sinne der Animationsaufgabe (s.o.), bei der es für ∆ i weniger auf eine sehr hohe Genauigkeit, sondern eher auf eine kurze Rechenzeit ankommt, wird die folgende Iteration durchgeführt (Notation in Pseudocode), bei der für die i-te Kugel der Wert von ∆ i ausgehend von 0 sukzessive in Schritten der Größe h erhöht wird, bis die obige Bedingung erfüllt ist:
δ k = 0
do while [ f (pi-1+ δ k) – f (pi-1) ]² + [ δ k ]² < 4 r²
δ k = δ k + h
loop
∆ i = δ k
p i = p i-1 + ∆ i
Hierbei ist der Parameter h in Bezug auf den Radius r hinreichend klein zu wählen.
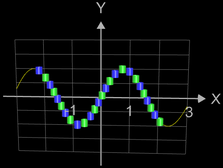
Als Beispiel soll die obige Funktion f (x) = t • sin (x) mit t = 0 bis 2.5 im Intervall [-2, 2] mit Kugeln dargestellt werden. Hierbei ist r = 0.2 und h = 0.005, es stehen 25 Kugeln zur Verfügung:
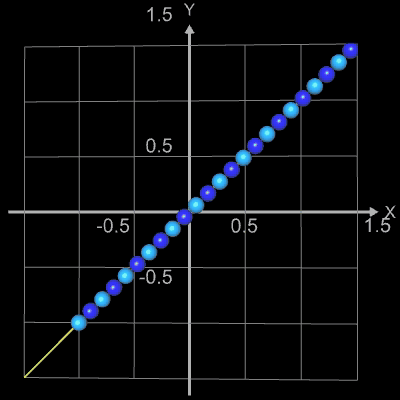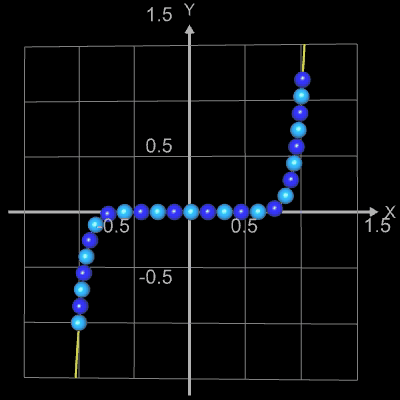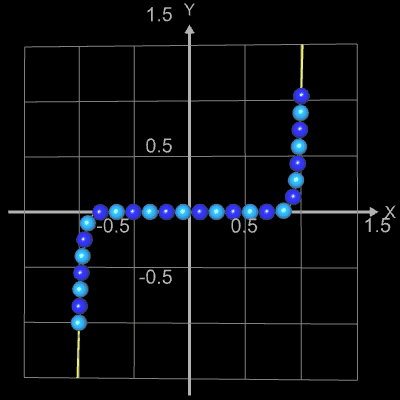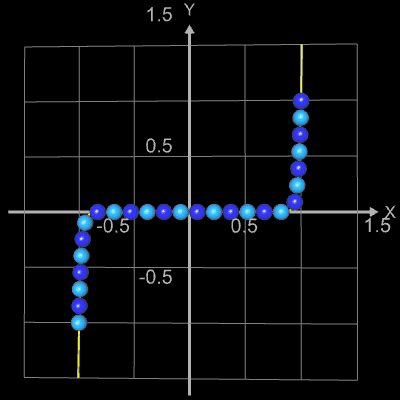
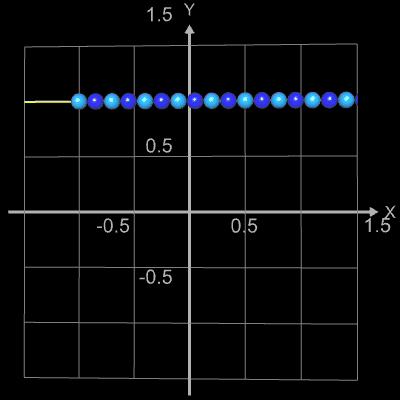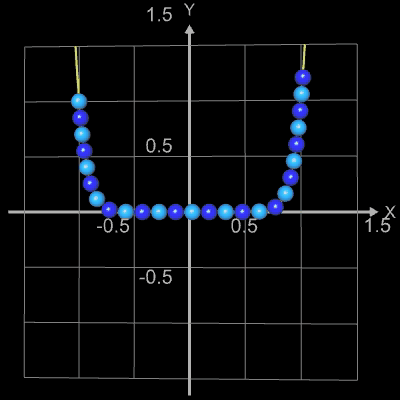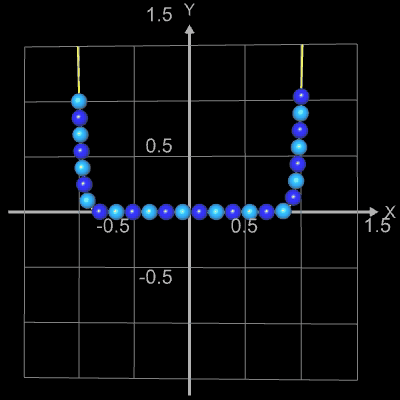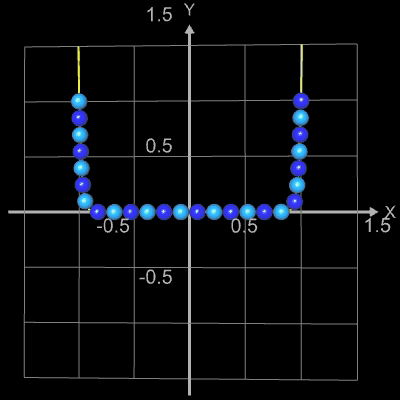
Die folgenden vier Abbidungten zeigen Beispiele für Funktionsgraphen mit jeweils 25 Kugeln, r = 0.065 und
h = 0.0001. Die beiden letzten Animationen zeigen die Funktionen f (x) = x2n+1
und f (x) = x2n
mit n = 0, 1, 2, ..., 20.
Für den Graphing Calculator 3D kann eine gc3-Datei, die einen Funktionsgraph aus Kugeln generiert, im Download-Bereich unten auf der Seite herunter geladen werden.
Als Variante des bisherigen Schemas wird der Radius r der 25 Kugeln automatisch an das darzustellende Intervall [a, b] angepasst, so dass das gesamte Intervall durch 25 Kugeln abgedeckt wird. Hierzu wird die Länge s des Funktionsgraphens im Intervall [a, b] ermittelt gemäß (s. auch Länge Funktionsgraph):
Für den Radius r einer Kugel wird dann die Länge s durch 2 • 25 geteilt. Die folgende Animation zeigt diese automatische Anpassung für die Funktion f (x) = - ex + 2 (gelbe Linie) im Intervall [a, 2], wobei die linke Intervallgrenze a (orange senkrechte Linie) in 0.5er Schritten den Bereich von -4 bis 1 durchläuft.
Funktionsgraph aus Kreisen
Das Schema für Kugeln lässt sich unmittelbar auf eine rein 2-dimensionale Version mit Kreisen übertragen. Die folgende Animation zeigt ein Beispiel mit automatischer Anpassung der Kreisradien.
Im folgenden soll der Funktionsgraph auch durch andere 3D-Objekte dargestellt werden ...
Funktionsgraph aus Würfeln
Der Funktionsgraph soll mit Würfeln dargestellt werden, deren räumliche Mittelpunkte auf dem Graph liegen. Dabei dürfen sich jeweils zwei aufeinander folgende Würfel nicht überschneiden. Vielmehr sollen sie sich mit einer ihrer Flächen oder ihrer Kanten berühren, wie - bis auf Symmetrie - die folgende Grafik zeigt:
Dazu wird die Bedingung in der oben angegebenen Iteration entsprechend angepasst:
δ k = 0
do until f (pi-1+ δ k) – f (pi-1) ≥ r or δ k ≥ r
δ k = δ k + h
loop
∆ i = δ k
p i = p i-1 + ∆ i
Hierbei ist r die Kantenlänge eines Würfels. Dieser wird als Super-Ellipsoid
erzeugt, da dieses bereits bei geringer Plot-Auflösung und entsprechend kurzer Rechenzeit einen präzisen Würfel liefert
(s. dazu auch Vergleich der Methoden bei Modellierung 3D
Würfel). Dazu im folgenden ein paar Beispiele (bitte zoomen):
Funktionsgraph aus Zylindern
Besteht die Kontur des Objekts in der x/y-Ebene nur aus waagerechten und senkrechten Linien, so kann die obige Bedingung für den Graph aus Würfeln leicht angepasst werden, wie z.B. für Zylinder mit der Höhe H und dem Durchmesser D in den folgenden Abbildungen (bitte zoomen):
...
do while f (pi-1 + δ k) – f (pi-1) < H nor
δ k < D
...
Die Zylinder werden als Parameterfläche erzeugt.
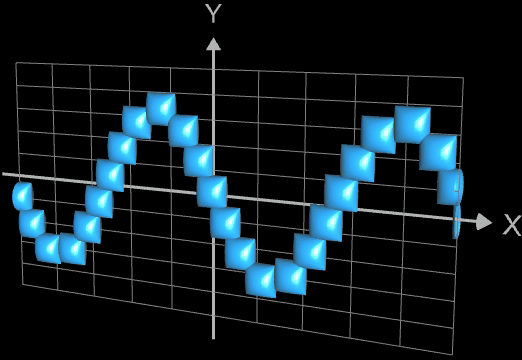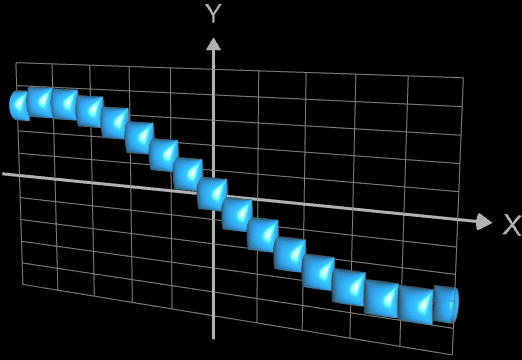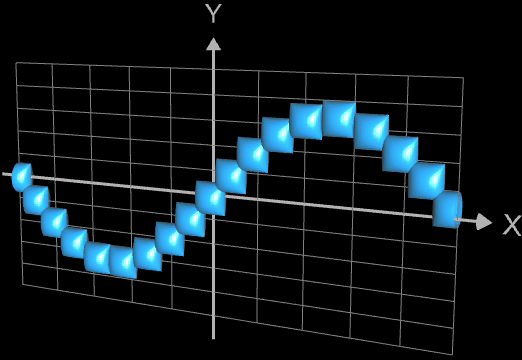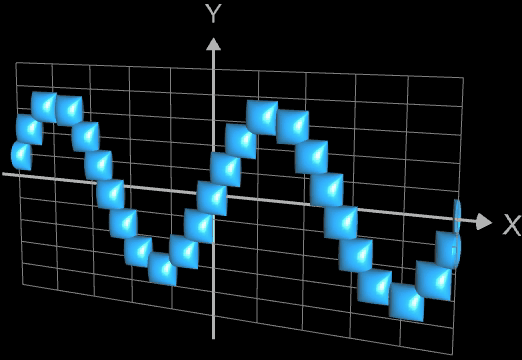
Nachfolgend eine Darstellung derselben Funktion mit quadratischen "3D-Kissen", die als Parameterfläche
f x (u, v) = r cos(u)
f y (u, v) = 0.8 r sin(u) sin(v)
f z (u, v) = r cos(v) mit u = 0, ..., π v = 0, ..., 2π
erzeugt werden. Wie der Zylinder auch besitzt das Kissen nur senkrechte und waagerechte Objektkonturen bei einer Kantenlänge von H = D = 2 r. Bei der Iteration gilt daher die gleiche Abbruchbedingung wie beim Graph aus Zylindern.
Funktionsgraph aus Kegeln
Der Funktionsgraph soll aus Kegeln der Höhe H und dem Radius r dargestellt werden; dabei soll der Graph durch die Schwerpunkte der Kegel verlaufen; diese werden als Parameterfläche erzeugt:
f x (u, v) = r u cos(v)
f y (u, v) = r u sin(v)
f z (u, v) = -H (-u + 2/3) mit u = 0, ..., 1 v = 0, ..., 2π
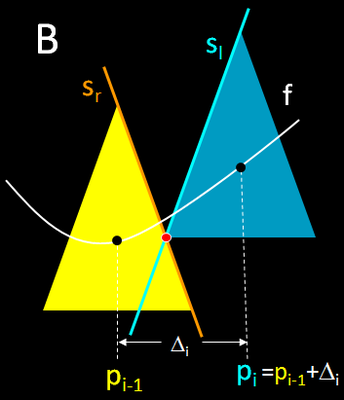
Der Schwerpunkt des (i-1)-ten Kegels liege auf dem Funktionsgraphen von f bei pi-1. Die korrekte Position des Schwerpunkts der folgenden i-ten Kegels in (pi | f (pi + ∆ i) soll bestimmt werden. Hierbei sind folgende Fälle zu berücksichtigen (vgl. folgende Schnittzeichnungen):
- der linke untere Rand des i-ten Kegels berührt die Mantelfläche seines Vorgängers (Grafik B)
- der rechte untere Rand des (i-1)-ten Kegels berührt die Mantelfläche seines Nachfolgers (Grafik C)
- die Spitze des (i-1)-ten Kegels berührt die Grundfläche des i-ten Kegels (Grafik E)
- die Spitze des i-ten Kegels berührt die Grundfläche des (i-1)-ten Kegels (Grafik F).
Um diese Fälle algorithmisieren zu können, werden für die Kegel jeweils die linke und rechte Mantellinie als Funktion sl bzw. sr in der x/y-Ebene aufgestellt. Ausgehend von pi-1 (Grafik A, D) wird für die Position des i-ten Kegels δ schrittweise um h solange erhöht, bis sl und sr sich in einem Punkt schneiden (roter Punkt in Grafik B und C) bzw. - bei steilen Verläufen des Graphs - der Abstand der Schwerpunkte (rote Linie in Grafik D) gleich H wird (roter Punkt in Grafik E und F).

Somit ergibt sich die folgende Abbruchbedingung bei der Iteration:
...
do until sli (pi + δ k - r) - sri-1 (pi-1 + δ k - r) ≥ 0
or sri (pi-1+ δ k - r) - sli-1 (pi-1 + δ k - r) ≥ 0
or | f (pi-1 + δ k) - f (pi-1) | ≥ H
...
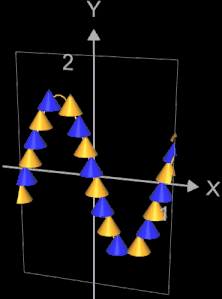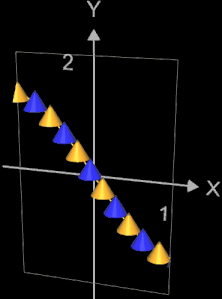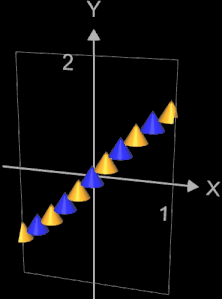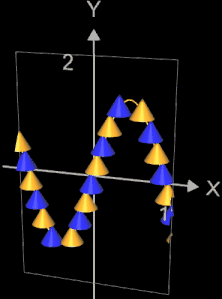
Die oben skizzierten möglichen Fälle bei der Anordnung der Kegel kann man gut in der rechten Grafik erkennen. Hier wird die Funktion
f (x) = 0.8 x4 – 2x2 im Intervall [-2, 2] mit Kegeln der Höhe H = 0.6 und Radius r = 0.3 dargestellt. Als Inkrement h bei der Iteration wurde der Wert 0.001 genommen.
Die folgenden linke Abbildung zeigt eine Animation für
f (x) = sin (t • x) im Intervall [-1, 1] mit t = -3.5, ..., 3.5.
In der folgenden rechten Abbildung wurde im Intervall [-2, 2] die Funktion f(x) = 1.8 exp (- t • x²) mit t = 0, ..., 4 und H = 0.2 sowie
r = 0.15 animiert. Hierbei wurde die Funktionskomponente fz (u, v) negativ gesetzt, so dass die Kegel mit der Spitze nach
unten zeigen.
Für den Graphing Calculator 3D kann eine gc3-Datei, die einen Funktionsgraph aus Kegeln generiert, im Download-Bereich unten auf der Seite herunter geladen werden.
Funktionsgraph aus beliebigen 3D-Objekten
Für beliebige Objekte mit krummliniger Kontur ist je nach Komplexität / "Kurvigkeit" des Objekts das Aufstellen der Bedingung für das Berühren zweier Objekte deutlich schwieriger als bei den zuvor verwendeten, geradlinig begrenzten Objekten.
Die beiden folgenden Grafiken zeigen den Sollzustand für die Funktion f (x) = sin (2x) bestehend aus "Sanduhren" bzw. transparenten "Schnecken". Im Gegensatz zu allen Beispielen zuvor wurden die Abstände der Objekte nicht automatisch berechnet, sondern vielmehr manuell per Schieberegler nach Augenmaß ermittelt.
Ein Ansatz für einen Algorithmus ist es, für zwei aufeinander folgende Objekte die Größe δ k solange zu iterieren, bis die Funktionen der Objektkonturen in der x/y-Ebene keine Schnittpunkte mehr aufweisen. Erste Versuche, die Schnittpunkte numerisch mit Hilfe des Newton-Verfahrens zu berechnen, waren bisher nicht so erfolgreich (z.B. Nichteindeutigkeiten, Wahl geeigneter Startwerte) und bedürfen weiterer Untersuchungen ...
Download