Tiruneh-Verfahren
Ein sehr interessantes und effizientes Verfahren, das auf dem Newton-Verfahren basiert, wurde 2013 von Tiruneh et al. vorgestellt [1]. Das Verfahren hat ein superquadratisches Konvergenzverhalten und liefert Ergebnisse auch in den Fällen, bei denen es mit dem Newton- oder Sekantenverfahren zu Problemen kommt, wie z.B. sehr langsame Konvergenz, Divergenz, Oszillation und Sprünge (aus dem Bereich der gesuchten Nullstelle heraus) oder "Absturz" des Newton-Verfahren, falls die Ableitung im Iterationspunkt den Wert 0 annimmt.
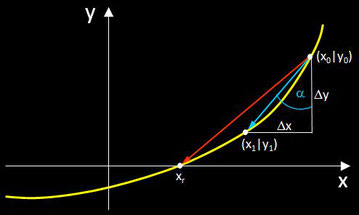
Bei diesem Verfahren wird außer dem Startpunkt
(x0
| f(x0)) noch ein weiterer Punkt (x1
| f(x1)) benötigt. Beide werden durch eine Linie verbunden, und es wird eine neue Variable m eingeführt, die identisch mit dem Cotangens des Winkels
α1
im entstehenden Dreieck ist (s. Grafik):
bzw. allgemeiner für alle Punkte (x | y) auf dem Funktionsgraphen
Als nächstes wird das Newton-Verfahren angewendet, wobei m als unabhängige Variable und y als abhängige Variable verwendet wird. Hiebei ist mr der Schätzwert der Nullstelle von y (m) = 0 mit dem entsprechenden Wert xr:
durch Einsetzen und Umformen aller beteiligten Größen (s. [1], S. 2-3) ergibt sich schließlich folgende Iterationsvorschrift:
mit i = 1, 2, 3, ...
Konvergenzbetrachtungen
Das Verfahren konvergiert superquadratisch, d.h. q = 1+√2 ≈ 2.414 (Beweis s. [1], S. 3). Bis auf den ersten Schritt mit der Berechnung zweier Funktionswerte werden pro Iterationsschritt ein Funktionswert und eine Ableitung berechnet, woraus sich eine Effizienz von CE = 1.554 ergibt.
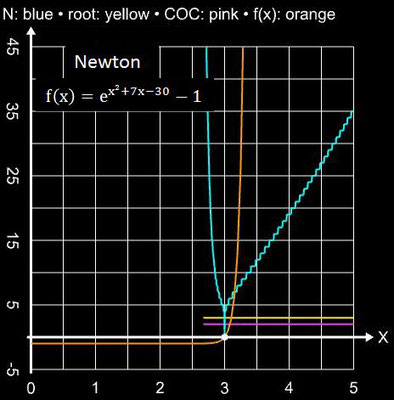
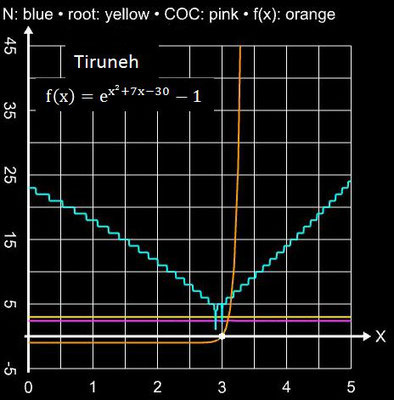
Als Beispiel hierzu soll die Nullstelle der Funktion f (x) = exp (x² + 7x - 30) - 1 für x ≥
0 mit dem Tiruneh- und zum Vergleich mit dem Newton-Verfahren bestimmt werden;
als Abbruchkriterium wurde
| xi – xi-1 | + | f(xi) | ≤ 10-15 gewählt. Wie man in der folgenden Galerie
erkennt, benötigt das Tiruneh-Verfahren weniger Iterationsschritte und hat einen deutlich größeren Einzugsbereich für den Startwert als das Newton-Verfahren.
Die superquadratische Konvergenz gilt nur für eine einfache Nullstelle; bei mehrfachen Nullstellen zeigt das Verfahren, wie alle anderen auch (s. Diverse Verfahren) außer dem Schröder-Verfahren (s. Konvergenz-betrachtungen beim Newton-Verfahren) ein lineares Konvergenzverhalten (q = 1).
Als Beispiel hierzu betrachte man die Funktion
f (x) = 0.125 (x+1) (x-3)2
mit der einfachen Nullstelle
ξ1 = -1 sowie der doppelten Nullstelle
ξ2 = 3 sowie die Funktion
f (x) = 0.125 (x+1) (x-3)4
mit der einfachen Nullstelle
ξ1 = -1 sowie der vierfachen Nullstelle
ξ2 = 3. Der Wert für d betrug 0.1, als Abbruchkriterium wurde
| xi – xi-1 | + | f(xi) | ≤ 10-15 gewählt.
Hinweis: Die Aussage in [1], S. 5 oben rechts, dass das Newton-Verfahren für die Funktion (x-1)6 - 1 lineare Konvergenz aufweist, während das Tiruneh-Verfahren superquadratisch konvergiert, ist falsch, da diese Funktion nur einfache Nullstellen besitzt und folglich beide Verfahren ihre typische Konvergenzordung (für Newton also q = 2) zeigen; die Verfasser wurden benachrichtigt und bestätigten den Fehler.
Beeinduckend ist die Stabilität des Verfahrens in der Nähe von Punkten, an denen die Anwendung des herkömmlichen Newton-Verfahrens zu Oszillation, Divergenz, Sprüngen zu entfernten Nullstellen oder Sprüngen außerhalb des Definitionsbereichs von f führen kann. Dies passiert typischerweise dann, wenn die Ableitung von f gegen den Wert 0 strebt.
Die Verfasser zeigen (s. [1], S. 4), dass im i+1-ten Iterationsschritt der Wert von xi+1 die gewichtete Summe der beiden Vorgänger xi und xi-1 ist. Der Gewichtungsfaktor sorgt dafür, dass die Iteration in die gewünschte Richtung verläuft: Falls das Verfahren gegen die Nullstelle konvergiert, wird der Gewichtungsfaktor für xi-1 nahezu 0 und für xi nahezu 1, so dass die Iteration weiterhin in Richtung der Nullstelle verläuft. Dagegen nimmt in der Nähe von Punkten, an denen die Ableitung der Funktion gegen 0 strebt, dieser für xi-1 nahezu den Wert 1 und für xi nahezu den Wert 0 an, so dass sich die Iteration vom Punkt xi wegbewegt.
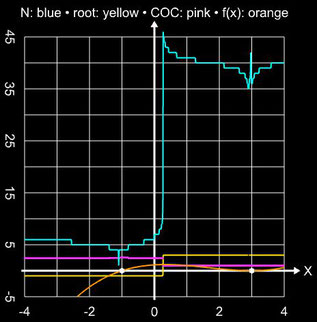
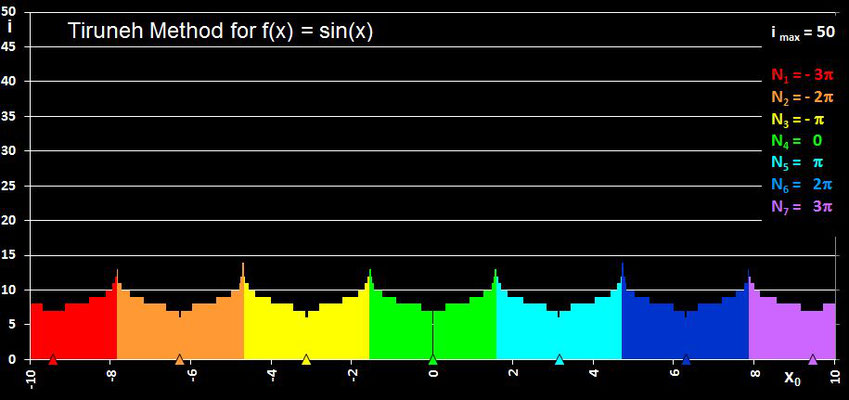
So zeigt das Verfahren (wie auch das Halley-Verfahren) z.B. für die Funktion f (x) = sin (x)
keine Sprünge zu entfernten Nullstellen, wie dies beim Sekanten- und Newton-Verfahren der Fall ist, sondern liefert die dem Startwert nächstgelegene Nullstelle, wie es im
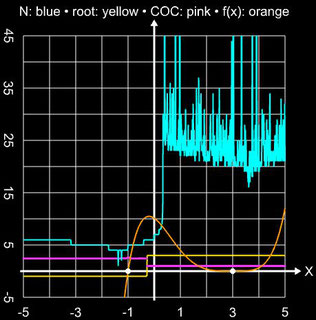
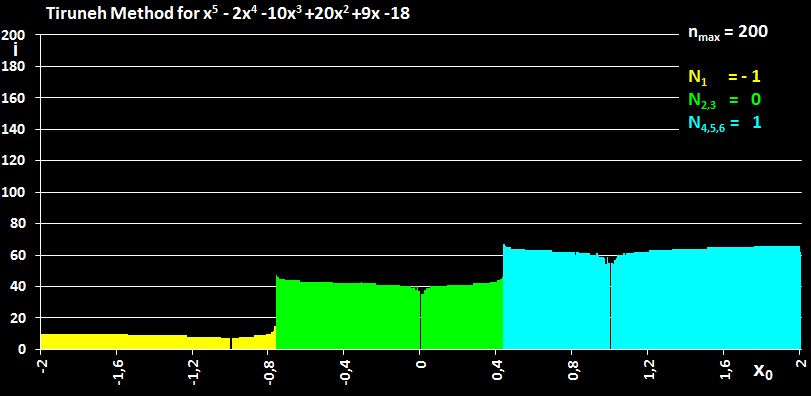
folgenden linken Diagramm zu sehen ist. Gleiches gilt für das Polynom
x5 - 2x4 - 10x3 + 20x2 + 9x -18 mit seinen Nullstellen bei -1 (einfach), 0 (doppelt) und 1 (dreifach) in der rechten Grafik.
In vielen Fällen, in denen das Newton-Verfahren und oftmals auch das Sekantenverfahren versagen, lässt sich mit dem Tiruneh-Verfahren dennoch ein Ergebnis erzielen. Dazu im Folgenden einige Beispiele (weitere finden Sie in [1], S. 6).
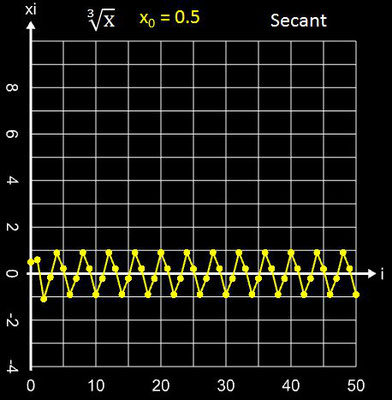
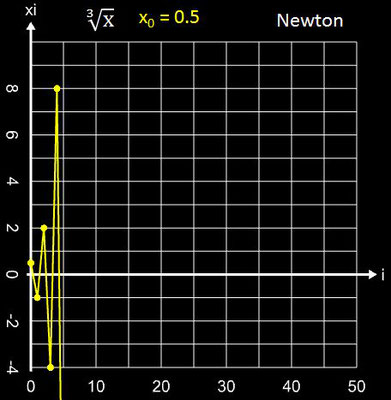
•
Gesucht ist die Nullstelle ξ = 0 mit Startwerten x0 aus [-1, 1]. Das Sekantenverfahren oszilliert im gesamten Intervall, während das Newton-Verfahren im gesamten Intervall oszillierend divergiert und dabei sehr schnell sehr große Werte annimmt (s. folgende Galerie am Beispiel für x0 = 0.5). Das Tiruneh-Verfahren liefert die gesuchte Nullstelle, wenngleich mit einer deutlich niedrigeren Konvergenzrate als sonst (COC ≈ 1).
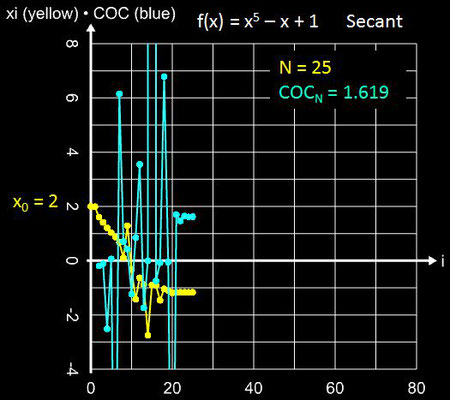
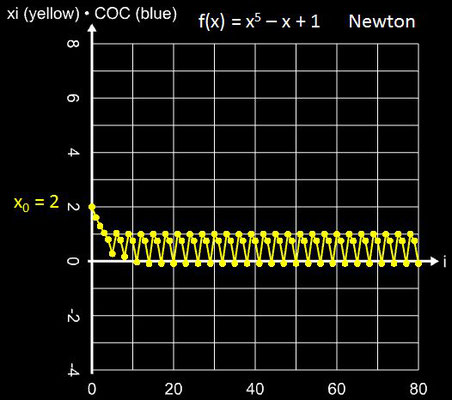
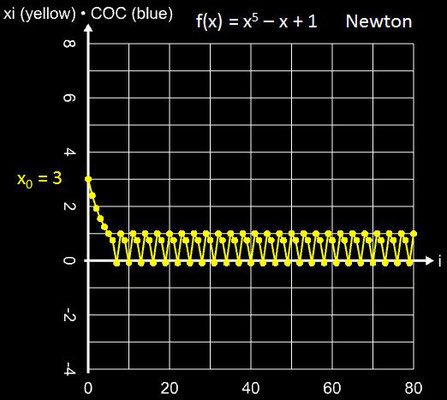
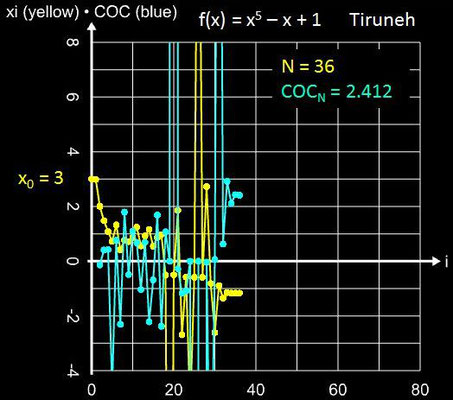
• x5 - x + 1
Die Nullstelle des Polynoms liegt bei ξ = -1.16730397826141... Mit dem Startwert x0 = 2 und d = 0.01 konvergieren das Sekanten- und Tiruneh-Verfahren, während das Newton-Verfahren oszilliert:
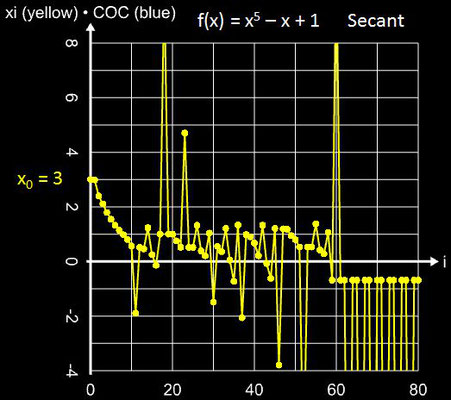
Mit x0 = 3 oszillieren sowohl das Sekanten- als auch Newton-Verfahren, während das Tiruneh-Verfahren die Nullstelle liefert:
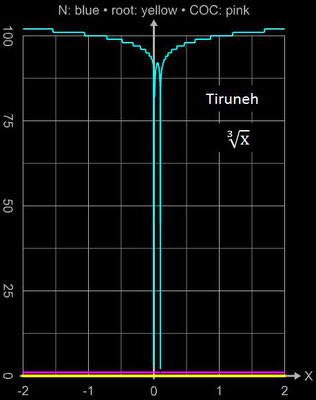
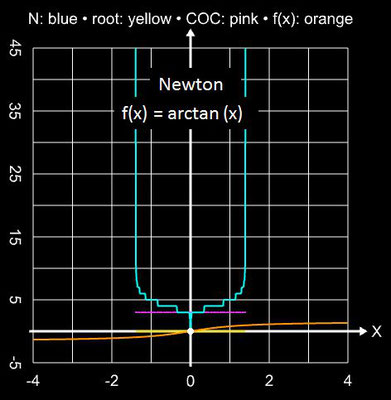
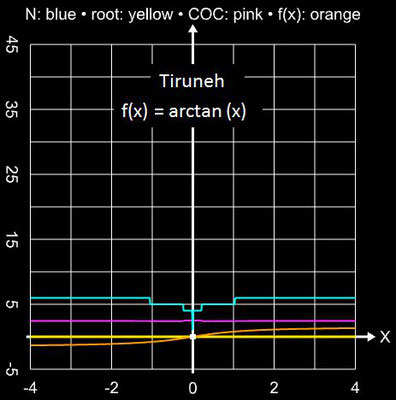
• arctan (x)
Während das Sekanten- und Newton-Verfahren begrenzte Einzugsbereiche für den Startwert besitzen (s. folgende Galerie) und außerhalb dieser divergieren, liefert das Tiruneh-Verfahren in wenigen Schritten die Nullstelle für den gesamten Bereich ]-∞, ∞[ \ {0}.
Quellenverweise
[1] Ababu Teklemariam Tiruneh et al. (2013), A Two-Point Newton Method Suitable for Nonconvergent
Cases and with Super-Quadratic Convergence, Advances in Numerical Analysis, Volume 2013,
http://dx.doi.org/10.1155/2013/687382