3D Brezel

Die Herleitung einer parametrischen "Brezelkurve" im Zweidimensionalen ist gar nicht so schwierig:

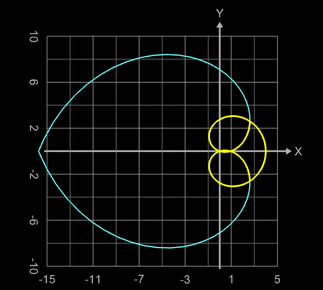
x (u) = (4 - 0.5 u²) cos(u)

y (u) = (4 - 0.5 u²) sin(u)     Parameterbereich für gelbe Brezelkurve:   u = - 3.92 ... 3.92    v = - π ... π

Hingegen bereitet die Übertragung ins 3-Dimensionale (im Prinzip ist die Brezel dann ein Ellipsoid) größere Probleme. Unterstützung fand ich bei der National Curve Bank der California State University, LA [1]:

mit  r₀ = 4   •   β = 0.5   •   a = 1   •   b = 5   •   u = - 4 ... 4   •   v = - π ... π

    Tipps:  

• Um eine einfache "Textur" mit Graphing Calculator 3D zu erzeugen, wird die erzeugte Oberfläche für alle (x,y)-Paare per Zufall etwas kleiner oder größer gemacht, quasi zufällig eingedellt bzw. angehoben.  Erreicht wird dies durch Addition des folgenden Terms zur  z-Komponente der erzeugenden Funktion: a (-1) ^{round( rand() )}, wobei der Faktor a Stärke und Aussehen der Dellen bestimmt und durch Ausprobieren ermittelt wird (z.B. hat a im zweiten Bild oben den Wert 0.002).

• Eine weitere Möglichkeit ist ein ungleichmäßiges Auftragen einer weiteren Farbe (weiss im rechten Bild oben). Hierzu wird die erzeugende Funktion zweimal hintereinander ausgeführt, ebenfalls mit einer additiven Zufallskomponente beim z-Anteil der Funktion. Durch Reduktion der Auflösung für die "Einfärbefunktion" werden so Pünktchen, Linien oder zusammenhängende Bereiche auf der Oberfläche erzeugt.

 Vom echten Objekt der Begierde ist das 3D Modell aber noch weit entfernt:

Quelle: http://www.romers.ch/de/content/grosser-laugen-brezel-40-stk

Quellen:

[1]   http://web.calstatela.edu/curvebank/pretzel79/pretzel79.htm  (ein Beitrag von Dr. Thomas Zettler)