Differential (Ableitung)

Oftmals benötigt man zur Lösung eines mathematischen Problems die Steigung einer Funktion f an einer bestimmten Stelle x₀  bzw. die Steigungsfunktion (Ableitung) f ', die zu jedem x-Wert aus dem Definitions-bereich von f die zugehörige Steigung von f liefert (z.B. beim Newton-Verfahren zur Bestimmung von Nullstellen oder bei der Volumenbestimmung von Rotationskörpern mit der Disc Method). Ob eine Funktion differenzierbar ist (d.h. ob deren Ableitung existiert) und daraus folgende Spezialfälle sollen hier nicht Gegenstand der Betrachtungen sein.

Zwar ist das Bestimmen der Ableitung f ' im Gegensatz zum Integrieren meist weniger aufwendig und erfolgt nach einigen wenigen Regeln (Faktor-, Summen-, Produkt-, Quotienten- und Kettenregel). Dennoch kann die Ableitung sehr komplex sein. Möchte man darauf verzichten, so kann man die Ableitung zu  f auch numerisch bestimmen bzw. approximieren (annähern).

Die Lösung hierzu bietet die Definition der Steigung einer Funktion f an der Stelle x₀ , nach der diese Steigung gleich der Steigung der Tangente im Punkt P (x₀ | f (x₀)) ist.

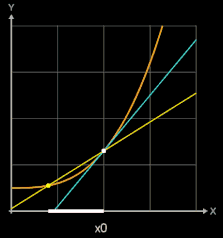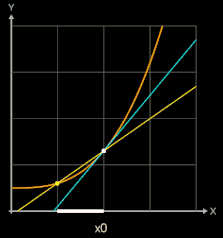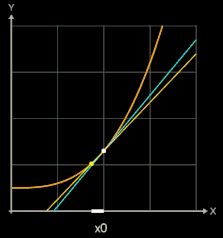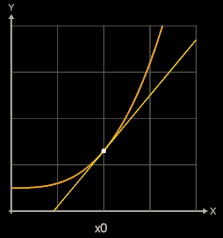
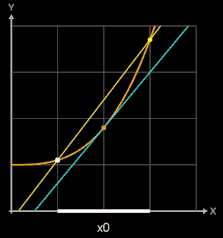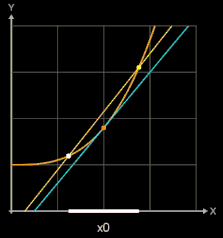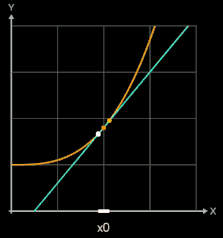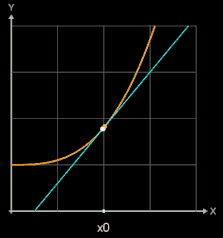
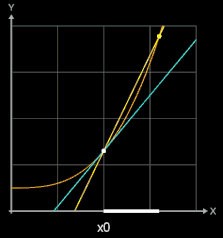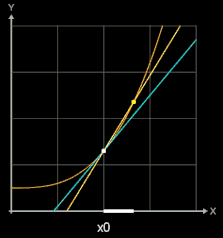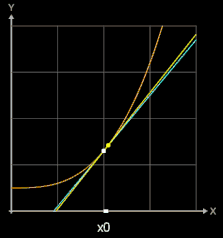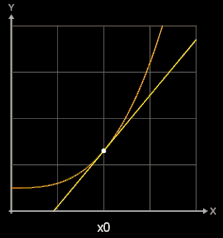
Zur Steigung der Tangente im Punkt P (x₀ | f (x₀)) (blau in folgenden Grafiken) gelangt man, indem man die Steigung einer Sekante  (gelb) durch P und einen weiteren Punkt Q (x₀+h | f (x₀)+h)) auf dem Graphen von f (braun)  bestimmt (sog. Differenzenquotient) und dann den Punkt Q immer näher an P heranrückt, indem man h gegen 0 laufen lässt.

Für h →0  geht dann bei diesem Grenzwertübergang die Sekante in die Tangente und somit die Sekantensteigung (Differenzenquotient) in die Tangentensteigung (Differentialquotient / Ableitung) über:

Da auf einem Rechner auf Grund der Zahlendarstellung eine untere Schranke für h existiert, kann der Grenzwertübergang nicht "in Gänze" durchgeführt werden; für die Ableitung gilt somit

bzw.

Es stellt sich natürlich die Frage, von welcher Größenordnung der Fehler ε in Abhängigkeit von h ist. Für den rechtsseitigen Differenzenquotienten entwickelt man dazu f an der Stelle (x + h) in eine Taylorreihe:

Der Fehler ist somit von der Ordnung O (h), d.h. mit linear kleiner werdendem h nimmt auch der Fehler linear ab. Analog hierzu ergibt sich auch für den linksseitigen Differenzenquotient die gleiche Ordnung
O (h).

Mit der Reihenentwicklung

ergibt sich für den zentralen Differenzenquotienten die Ordnung O (h²), d.h. der Fehler nimmt mit linear kleiner werdendem h quadratisch ab.

Die folgenden Grafiken zeigen Beispiele, die mit Graphing Calculator 3D berechnet wurden.

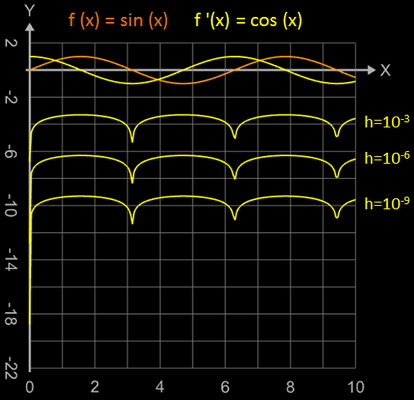
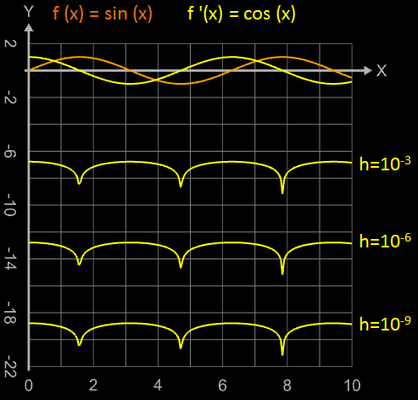
In der linken Grafik wurde für die Funktion f (x) = sin (x) der rechtsseitige Differenzenquotient für verschiedene Werte von h berechnet und der resultierende lineare Fehler ε auf der y-Achse dargestellt. In der mittleren und rechten Grafik wurde der zentrale Differenzenquotient und der sich ergebende quadratische Fehler ermittelt.

Hinweis: Um die sehr kleinen Werte der Fehler sowie die Funktion selbst im gleichen Koordinatensystem darstellen zu können, wurde in allen drei Grafiken der Fehler logarithmisch berechnet gemäß

und auf der y-Achse logaithmisch dargestellt.

Übrigens ...

Das Ersetzen der Ableitung durch den Differenzenquotienten findet bei einigen Verfahren zur numerischen Nullstellenbestimmung statt (z.B. Steffensen-Verfahren, Jain-Verfahren, s. unter Nullstellenbestimmung reeller Funktionen / Diverse Verfahren) - in erster Linie, um den Effizienzindex CE zu erhöhen, da außer den Funktionswerten nicht auch noch die Werte der Ableitung(en) berechnet werden muss.

Ebenso wie die erste Ableitung durch Differenzenquotienten approximiert werden kann, gilt dies auch für höhere Ableitungen, indem man die Methode der Reihenentwicklung anwendet:

Für die beiden nächsthöheren Ableitungen ergibt sich:

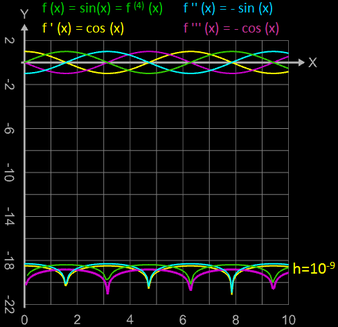
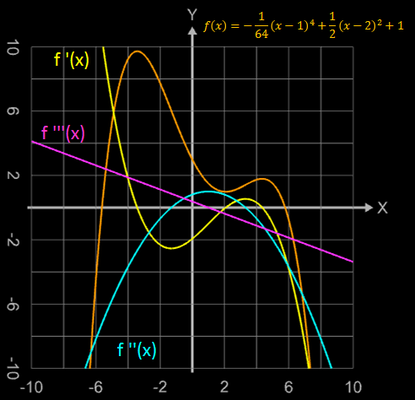
Die folgende Grafik zeigt die so berechneten ersten vier Ableitungen der Funktion f sowie den resultierenden quadratischen Fehler von ca. 10^-18 mit h = 10^-9.

Bei der Wahl von h zur Berechnung der n-ten Ableitung (bzw. Differenzenquotienten) ist zu beachten, dass dabei jeweils durch hⁿ geteilt wird. Beim Graphing Calculator 3D und der voreingestellten mathematischen Standardbibliothek "Double" liegt die interne Rechengenauigkeit bei "nur" 10^-15, so dass h nicht zu klein gewählt werden darf. Als Anhaltspunkt für die Größenordnung von h gilt hier:

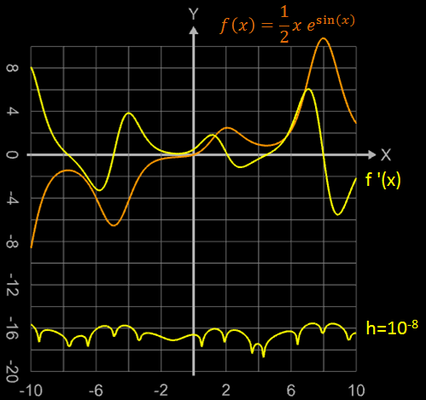
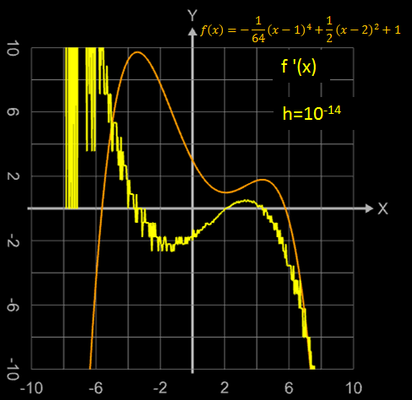
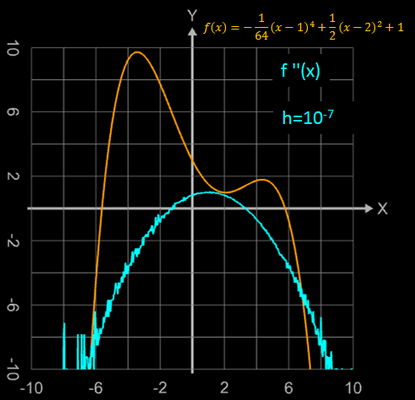
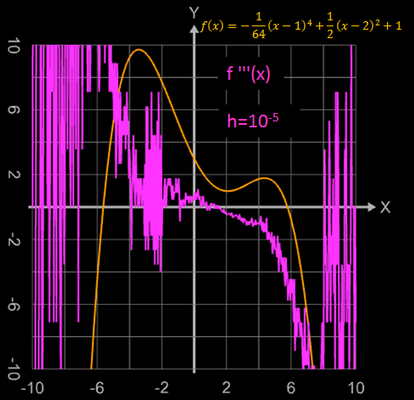
Die folgenden Grafiken zeigen die auftretenden Fehler, wenn h um eine Zehnerpotenz kleiner gewählt wird, als die zuvor angegebene untere Schranke für h.

Reicht die so erzielte Genauigkeit nicht aus, kann man in Graphing Calculator 3D die mathematische Bibliothek "APfloat" verwenden und die Anzahl der Digits (Nachkommastellen) entsprechend hoch einstellen (einige der Grafiken ganz oben wurden so erzeugt).

Dies hat wohl zur Folge, dass sich die Rechenzeit deutlich erhöht.  In der Praxis ist daher abzuwägen, ob die mit der Standardbibliothek erreichte Genauigkeit nicht ausreichend ist, zumal der auftretende Fehler beim Berechnen der Ableitungen von der Ordnung  O (h²) ist und oftmals auch nur die erste Ableitung einer Funktion benötigt wird ...