3D Rotationen um Koordinatensystem-Achsen

Die meisten dreidimensionalen Objekte / Flächen auf meiner Webseite werden durch eine parametrische Funktion

mit den Parametern u und v erzeugt.

Möchte man ein solches Objekt / Fläche in einem 3D-Koordinatensystem verschieben (sog. Translation), muss man zu den x-, y- und z-Komponenten f_x, f_y, f_z der Funktion f lediglich den entsprechenden Wert der Verschiebung in die jeweilige Richtung (t_x, t_y, t_z ) addieren:

Soll das Objekt / Fläche hingegen um eine oder gar um alle drei Achsen eines Koordinatensystem gedreht werden (Rotation), ist der Aufwand ein wenig größer. Hierzu betrachte man einen Bildpunkt (x | y | z) des Objekts / Fläche als Vektor, der um den Winkel θ gedreht werden soll; der gedrehte Bildpunkt (x' | y' | z') ergibt sich durch die Multiplikation des Vektors mit einer Rotationsmatrix R (θ):

Als Beispiel für die Herleitung der Rotationsmatrix betrachte man die Rotation um die z-Achse. Hierbei gilt:

• z ' = z                            (da um die z-Achse gedreht wird)
• x ' =   x cos α + y sin α
• y ' = - x sin α + y cos α

Hieraus folgt die unten angegebene Rotationsmatrix R_x (α_x).

Im folgenden sind für die drei möglichen Rotationen um die Koordinatenachsen im Raum die erforderlichen Rotationsmatrizen und Berechnungen mit den Drehwinkeln α_x , α_y und α_z für die jeweilige Achse angegeben (aus Gründen der Übersichtlichkeit wurde auf den Term "(u, v)" bei den Komponenten der Funktion f verzichtet):

Rotation um die x-Achse:                Rotation um die y-Achse:                    Rotation um die z-Achse: 

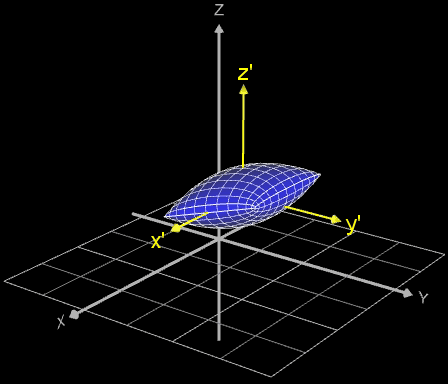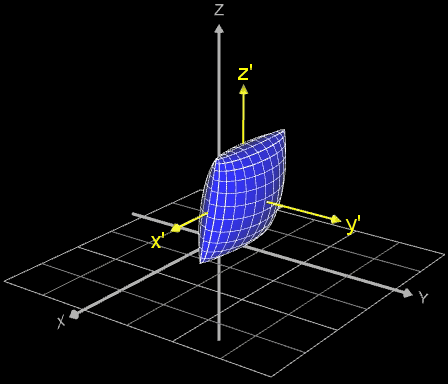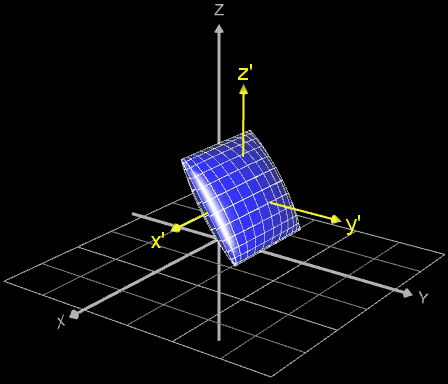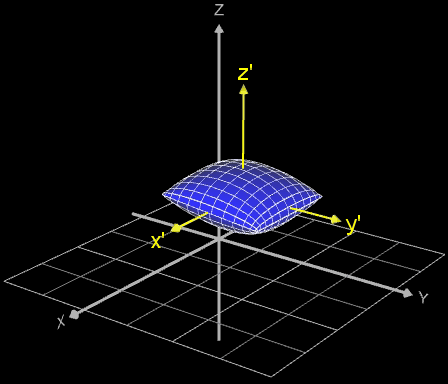
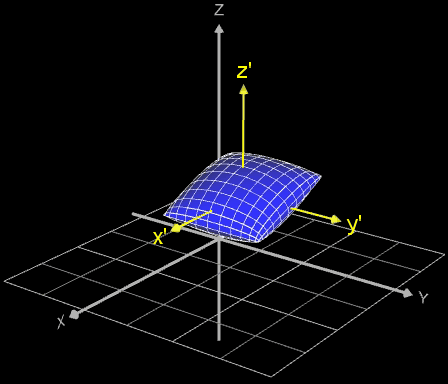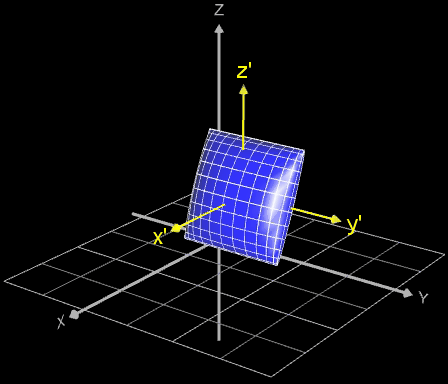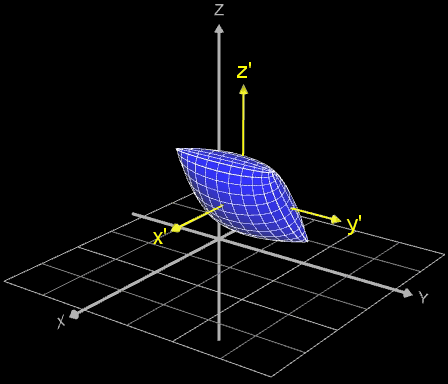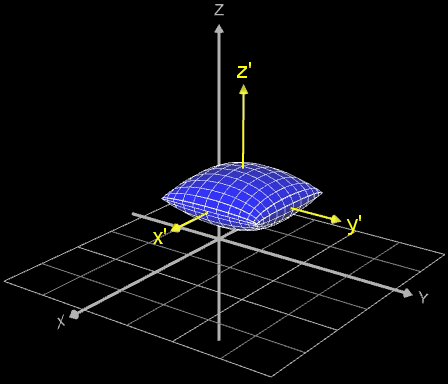
Falls die gleiche Art der Rotation durchgeführt werden soll, wobei sich der Mittelpunkt des Objekt/Fläche aber nicht im Ursprung des Koordinatensystems befindet, sondern im Punkt ( ∆x | ∆y | ∆z) wie in den folgenden Beispielen (weitere Anwendung s. Funktionsgraph als Rohr / Röhre):

so sind die Koordinaten ∆x, ∆y, ∆z komponentenweise beim jeweiligen Rotationsvektor hinzu zu addieren.

Dies entspricht einer Verschiebung des Koordinatensystem zum neuen System x', y', z' (gelb in Animation).   

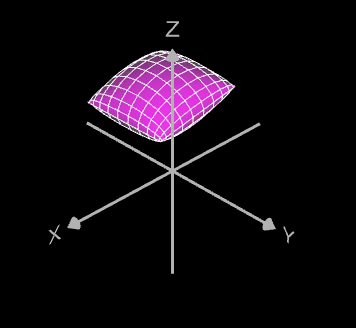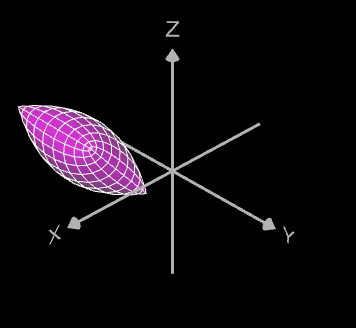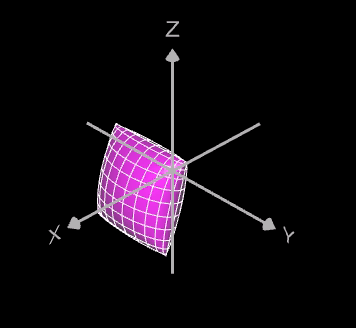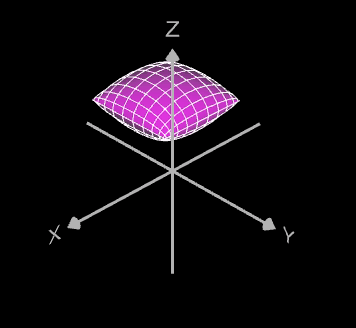
Bei den folgenden Beispielen wurde das Objekt vor der Rotation in x-, y- und z-Richtung verschoben, d.h. die Verschiebung erfolgt in der Objektfunktion:

die dann entsprechend rotiert wird:

Soll ein Objekt/Fläche um alle drei Achsen des Koordinatensystems mit den entsprechenden Drehwinkeln
α_x , α_y und α_z gedreht werden, so kann die Rotation z.B. folgendermaßen ausgeführt werden: 

Mit Hilfe der Graphing Calculator 3D-Datei Rotations about x y z Axis.gc3 kann dies leicht bewerkstelligt werden. Hier sind lediglich die Objektfunktion f und die Bereiche für u und v einzugeben. Die Werte für die Translation (t_x, t_y, t_z ) und für die Drehwinkel (α_x , α_y und α_z) können bequem mittels Schiebereglern eingestellt werden. Mit dem Parameter rot_speed kann man die Geschwindigkeit einstellen, falls die Rotation animiert werden soll .

Beeindruckend zeigt sich Graphing Calculator 3D, wenn man das Objekt gleichzeitig um mehrere Achsen drehen lässt:

Es sei noch angemerkt, dass Graphing Calculator 3D per se die Möglichkeit bietet, das gesamte Koordinatensystem mit dem geplotteten Objekt per gedrückt gehaltener Maustaste "im Raum" zu drehen, um sich dieses von allen Seiten anschauen zu können.