Kreise verbinden
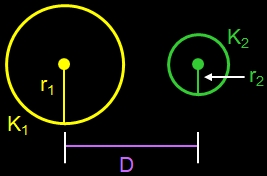
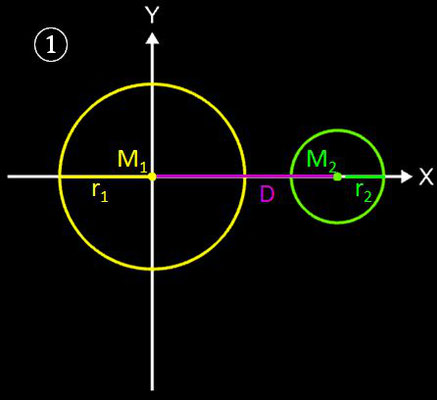
Gegeben sind zwei Kreise mit den Radien r1 und r2 und dem Mittelpunktsabstand . Die beiden Kreise sollen nun verbunden werden durch eine
1. Kreise mit äußeren Tangenten verbinden
Die beiden Kreise sollen nun durch eine von außen an beide Kreise angelegte, gemeinsame Tangente
t verbunden werden (s. Grafik rechts).
Diese Aufgabenstellung ergibt sich z.B. bei der Konstruktion eines Riementriebs oder einer straff gespannten Fahrradkette.
Eine Herleitung der benötigten Größen für die Tangente t an beide Kreise, für die Berührpunkte A und B und die daraus resultierende Teilstrecke g der Tangente
t ebenso wie einige Beispiele finden Sie unter
3D Mathe/3D Objekte/Riementrieb (Transmission).
2. Kreise mit inneren Tangenten verbinden
Für die Kreise K1 und K2 mit den Mittelpunkten M1 und M2 und Radien
r1 und r2 soll die innere Tangente
t (x) = m x + y0 hergeleitet werden, wobei oBdA M1 im Nullpunkt eines Koordinatensystems liegt.
Geometrische Lösung
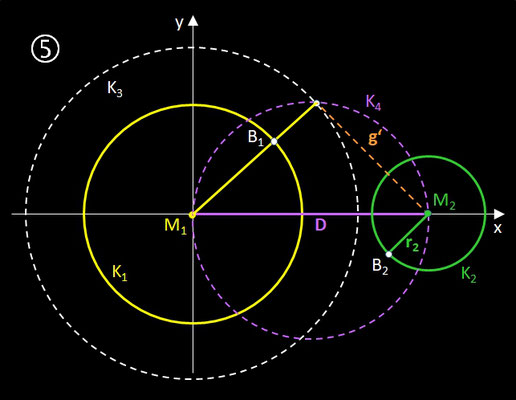
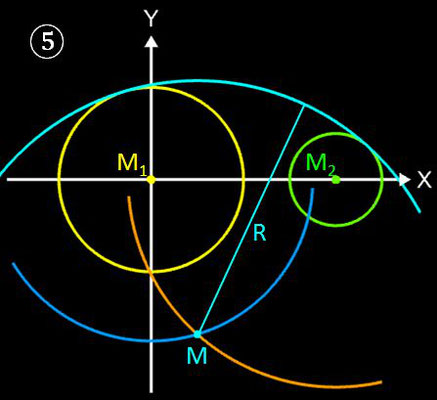
Die folgenden Arbeitsschritte stellen eine geometrische Lösung dar. Die Nummern der Schritte korrespondieren mit den numerierten Grafiken in der nachfolgenden Galerie.
- Zeichne um M1 von Kreis K1 einen Kreis K3 mit dem Radius r1 + r2.
- Zeichne den Thales-Kreis K4 über die Verbindungslinie D der Mittelpunkte M1 und M2.
- Verbinde den Schnittpunkt von K3 und K4 mit dem Mittelpunkt M1 und erhalte den Berührpunkt B1 als Schnittpunkt von K1 und dieser Verbindungsgeraden.
- Verbinde den Schnittpunkt von K3 und K4 mit dem Mittelpunkt M2 und erhalte die Stecke g'.
- Zeichne die Senkrechte zu g' durch M2 (Parallele zu M1B1) und erhalte als Schnittpunkt mit dem Kreis K2 den Berührpunkt B2.
- Die Gerade durch B1 und B2 ist die gesuchte innere Tangente t.
Analytische Lösung
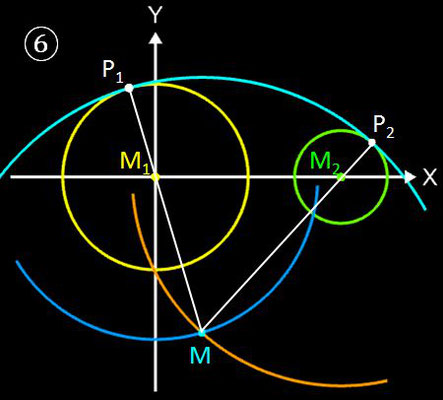
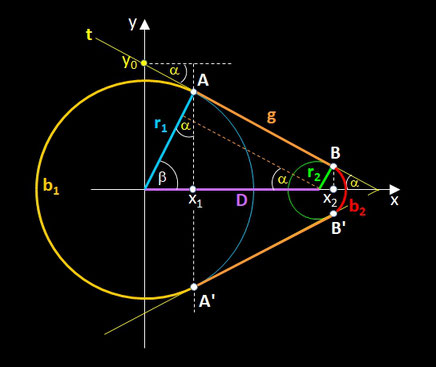
Für eine analytische Lösung betrachte man die folgende Grafik.
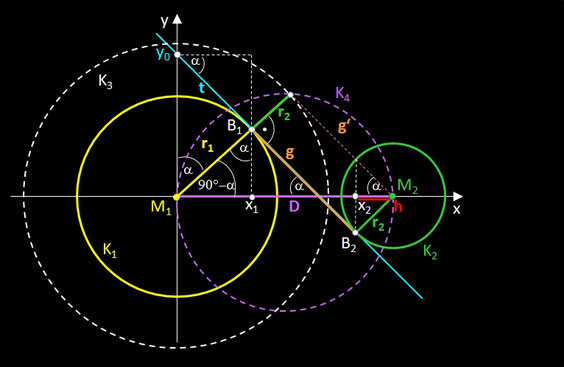
Es gelten folgende Beziehungen:
Die x-Koordinaten x1 und x2 der Berührpunkte B1 und B2 ergeben sich zu
Die Länge der Strecke g zwischen B1 und B2 auf der Tangente t beträgt:
.
Die folgende Animation zeigt für zwei Kreise die inneren Tangenten t und t' (weiß) und die Streckenabschnitte g und g' (orange) auf den Tangenten, wobei der Abstand D (lila) animiert wird.
Eine typische Anwendung für die Verbindung zweier Kreise mit inneren Tangenten ist ein Riementrieb mit gekreuztem Riemen, um z.B. eine Drehbewegung umzukehren (s. 3D Mathe/3D Objekte/Riementrieb).
3. Kreise mit tangentialen Kreisbögen verbinden
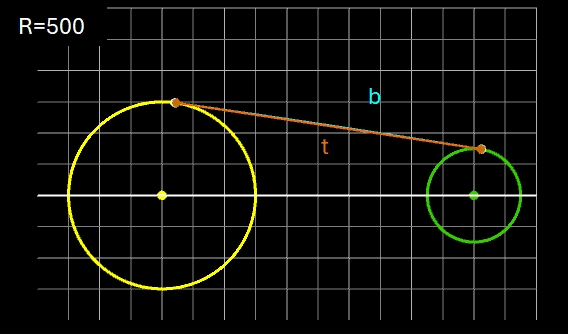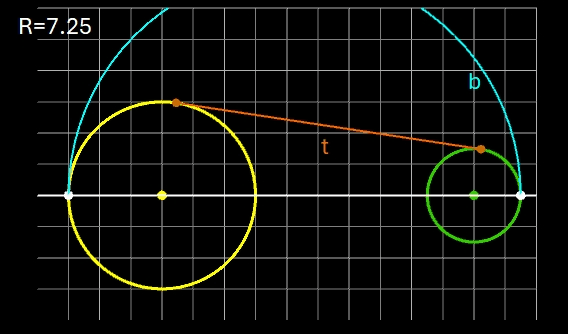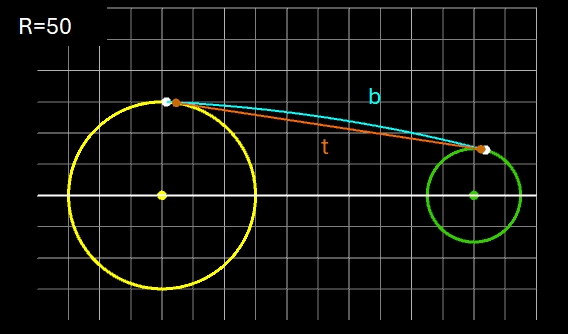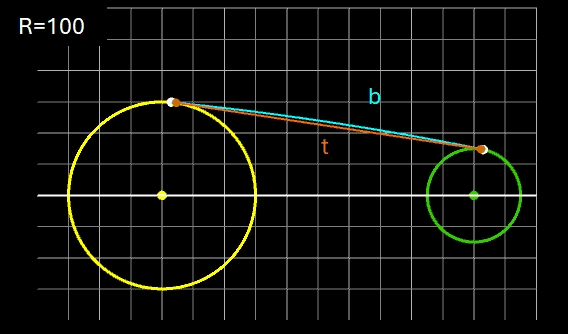
Eine andere Verbindung soll durch einen von außen an beide Kreise angelegten Kreisbogen b mit gegebenem Radius R derart erfolgen, dass der Kreisbogen die beiden Kreise jeweils tangential in genau einem Punkt berührt.
Dies kann z.B. bei der Konstruktion von Nocken einer Nockenwelle angewendet werden. Ebenfalls können so Ei-Kurven (s. 3D Ei) konstruiert werden.
Für R gilt die Bedingung:
Wo liegt der Mittelpunkt M dieses Verbindungskreises, wie lauten die Koordinaten der Berührpunkte?
Geometrische Lösung
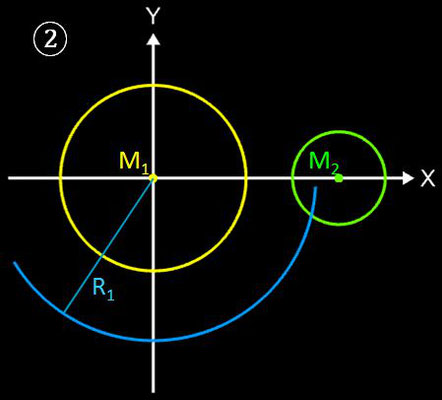
Die folgenden Schritte stellen eine geometrische Lösung dar. Die Nummern der Schritte korrespondieren mit den numerierten Grafiken in der nachfolgenden Galerie.
- Ausgangssituation
- Schlage um M1 einen Kreis mit Radius R1 = R – r1.
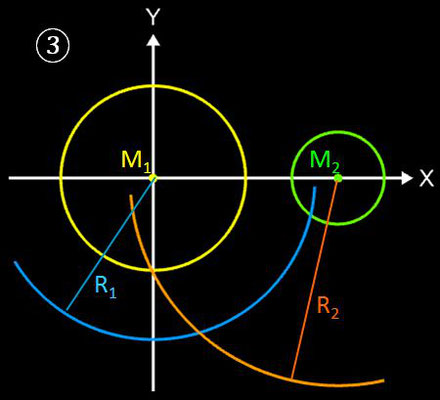
- Schlage um M2 einen Kreis mit Radius R2 = R – r2.
- Schnittpunkte der Kreise ist der Mittelpunkt M des gesuchten Kreisbogens b.
- Schlage um M einen Kreis mit Radius R
- Anschlusspunkte P1 und P2 ergeben sich durch die Geraden M-M1 bzw. M-M2
- fertige Lösung
Analytische Lösung
R1 = R – r1 R2 = R – r2
Abschließend noch einige Beispiele, bei denen die Parameter D, r2 bzw. R variiert werden:
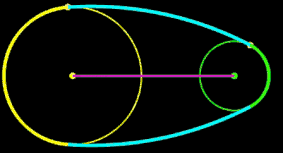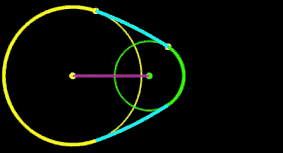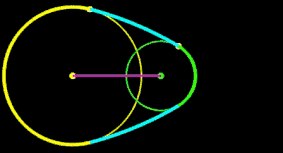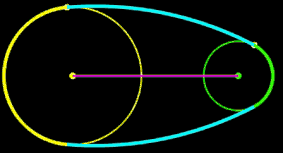
r1, r2 ,R: fix D: variabel
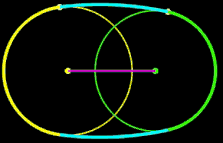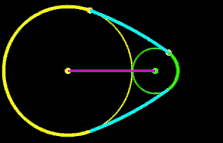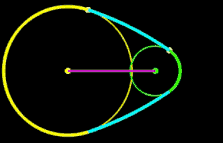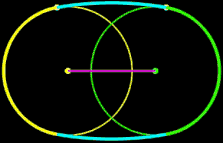
r1, R, D: fix r2: variabel
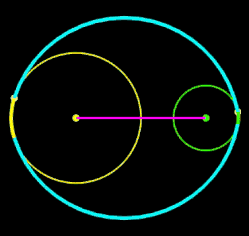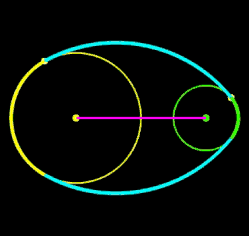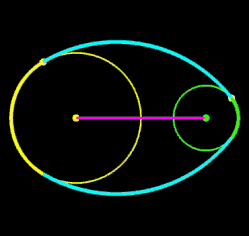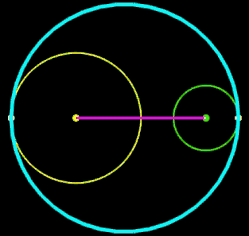
r1, r2 ,D: fix R: variabel
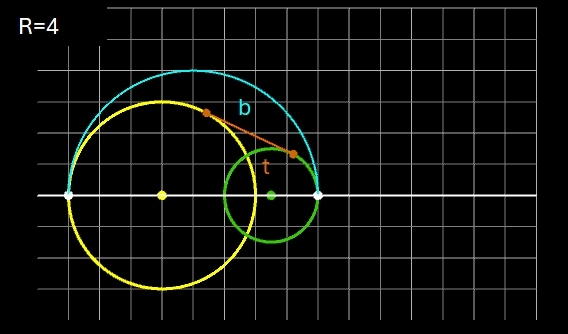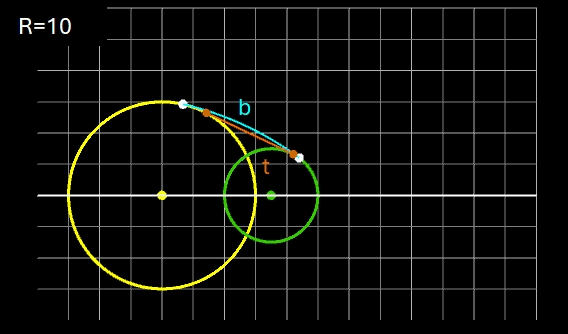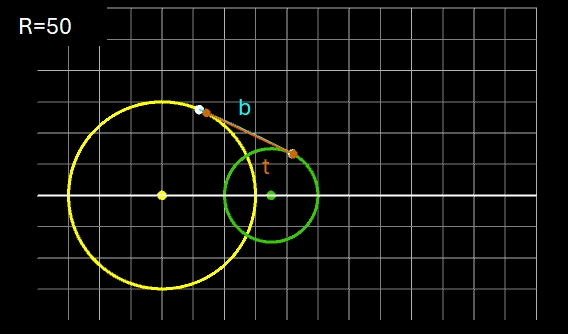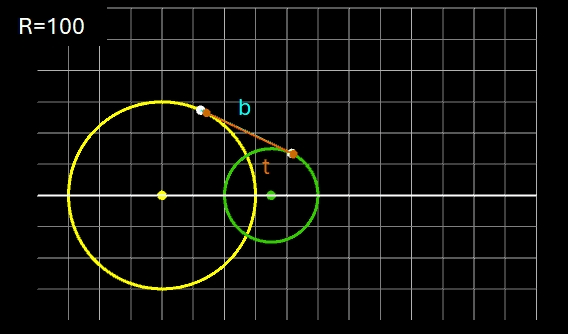
Für zwei Kreise mit dem Mittelpunktsabstand D gilt: je größer R desto mehr nähert sich der Kreisbogen b dem Tangentenabschnitt t. Liegen die Kreise weiter auseinander, so kann muss man für R im Vergleich zu den Kreisradien schon sehr hohe Werte einsetzen, um sich t anzunähern. In den beiden folgenden Animationen wird dies beispielhaft gezeigt; dabei hat ein Kästchen die Größe 1 x 1.
4. Kreise mit tangentialen Kreisbögen durch Punkt Q verbinden
Eine Erweiterung der vorherigen Aufgabe besteht darin, dass der von außen an beide Kreise angelegte Kreisbogen b zusätzlich durch einen Punkt Q (p | q) verläuft. Dabei werden die Koordinaten p und q vorgegeben, die Mittelpunktskoordinaten für M und der Radius R für b müssen ermittelt werden.
Grundsätzlich sind die folgenden Szenarien (Zwei-Kreis-Figuren) für die Anordnung möglich:
Da der durch Q verlaufende Kreisbogen b die beiden Kreise jeweils in genau einem Punkt berühren soll, kann Q nicht völlig beliebig gewählt werden.
Näherungslösung
Ein erster Lösungsansatz ist die Iteration von R, d.h. ausgehend von Rmin wird R erhöht, bis die Strecke MQ ungefähr gleich groß wie R ist. Die folgenden Animationen zeigen dazu ein paar Beispiele, wobei der rote Punkt Q sich auf verschiedenen Wegen bewegt. Der erscheinende "einsame" cyan-farbene Punkt ist der Mittelpunkt M des Kreisbogens b.
Im Folgenden soll eine allgemeine Lösung in geschlossener Form hergeleitet werden...
Standardfall
Für die Herleitung einer Lösung in geschlossener Form betrachte man zunächst den folgenden "Standardfall".
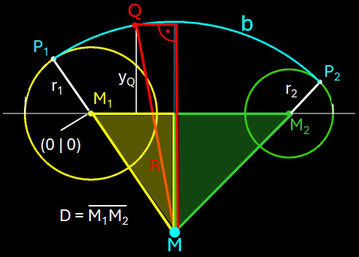
Die Kreise mit den Mittelpunkten M1 und M2 haben die Radien r1 und r2, wobei M1 oBdA im Nullpunkt eines Koordinatensystems liegt und D den horizontalen Abstand der Mittelpunkte darstellt. Für einen Punkt Q (p | q), der entweder außerhalb beider Kreise oder innerhalb der "Linse" bei sich überlappenden Kreisen liegt, sind für den tangentialen Bogen b die Koordinaten seines Mittelpunktes M (xM | yM) und sein Radius R gesucht.
Für alle diese Größen lassen sich mittels rechtwinkliger Dreiecke (vgl. mit Grafik) folgende Beziehungen aufstellen:
∆ (xM - xQ)²+ (yM - yQ)² = R²
∆ xM² + yM ² = (R - r1)²
∆ (D - xM)² + yM² = (R – r2)²
Zur Lösung dieses nichtlinearen Gleichungssystems habe ich WolframAlpha "bemüht". Mir war klar, dass die allgemeinen Lösungen keine Einzeiler sein würden, aber das Resultat hat mich dann doch überrascht...
Bis auf Spezialfälle (s. u.) gibt es stets die obigen beiden Lösungen, wobei sich die zweite Lösung dadurch ergibt, dass an den rot markierten Stellen die Vorzeichen der Quadratwurzel invertiert werden.
In den folgenden Galerien sollen verschiedene Szenarien mit diversen Kreisen und Plazierungen von Q aufgezeigt werden. Für die Grafiken gilt dabei die folgende Zuordnung:
¤ : Kreis1
¤ : Kreis2
• : Punkt Q (p | q)
¡, ¡ : Lösungskreise
+, + : Mittelpunkte der Lösungskreise
•,
•
: Endpunkte der Lösungsbögen
------- : Tangente an Kreis1 und Kreis2
r1 = r2 , r1² ≠ q² , D ≠ 0
Falls die Kreise gleich groß sind, der Punkt Q jedoch nicht auf einer der Tangenten an die beiden Kreise liegt, gilt die folgende Lösung.
r1 = r2 = q , r1 D p ≠ r1 p²
In diesem Fall liegt Q auf einer der Tangenten an die beiden gleich großen Kreise. Dadurch reduziert sich die Berechnung zu:
q = 0 , r1 D + r2 p ≠ r1 p
Die folgenden Gleichungen ergeben sich, falls Q auf der x-Achse liegt.
5. Kreise mit Übergangskurve verbinden
Eine weitere Art, zwei Kreise miteinander zu verbinden, sind Übergangskurven.
Im Bereich des Computerdesigns verwendet man als Übergangskurven vorzugsweise implizite Kurven, um die geometrische Stetigkeit (Begriff aus der Geometrischen Modellierung [1]) zu realisieren, wobei insbesondere die G2-Stetigkeit angestrebt wird, d.h. dass unabhängig von der Darstellungsart (parametrisiert, implizit, explizit) Übergangskurve und Kreis im Berührpunkt dieselbe Tangente und dieselbe Krümmung haben.
In der folgenden Animation werden zwei Kreise f1 und f2 in impliziter Form durch eine implizite Übergangskurve F verbunden. Weitere Informationen hierzu finden Sie unter Übergangskurven.