Iteration

Allgemein beschreibt Iteration einen Prozess mehrfachen Wiederholens gleicher oder ähnlicher Handlungen zur Annäherung an eine Lösung oder ein
bestimmtes Ziel. Jede Wiederholung des Prozesses wird auch als "Iteration" bezeichnet, wobei die Ergebnisse einer Iteration als Startpunkt für die nächste Iteration verwendet werden.
Als einfaches Beispiel sei hier die Aufgabe genannt, die Summe aller natürlichen Zahlen 1 bis 20 zu bestimmen. In Pseudocode ist dann die folgende Iteration auszuführen:
i = 1
sum = 0
do while i <= i max
sum = sum + i
i = i + 1
loop
Eine solche Schleife lässt sich mit Graphing Calculator 3D nicht realisieren. Dafür steht aber ein anderes mächtiges Werkzeug zur Verfügung: es lassen sich rekursive Funktionen definieren. Eine Iteration muss somit in eine Rekursion überführt werden. Die Berechnung der Summe im Beispiel lässt sich dann so formulieren:
Rekursion:
Lösung mit GC3D:
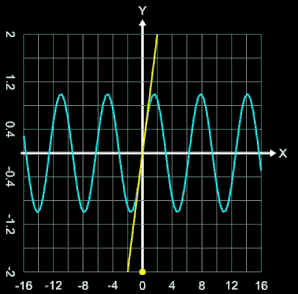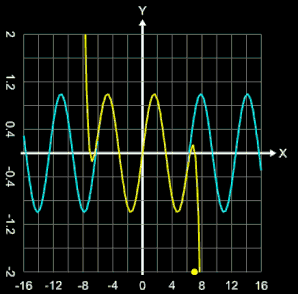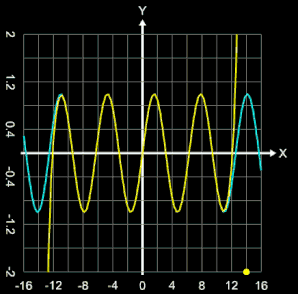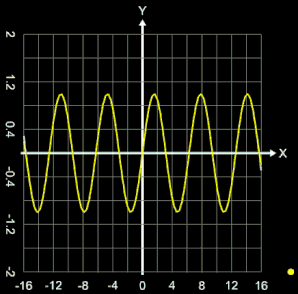
Ein weiteres Beispiel sei die Annäherung der Funktion
f (x) = sin (x) mit einer Taylor-Reihe. Es gilt:
mit folgender Umsetzung in GC3D:
Der wandernde gelbe Punkt in der Animation rechts zeigt die jeweilige Anzahl n an Iterationen.
Zu beachten ist, dass bei beiden Beispielen die Anzahl auszuführender Iterationen zur Berechnung des Ergebnisses fest vorgegeben ist.

In der numerischen Mathematik steht der Begriff Iteration für eine Methode, sich der exakten Lösung eines Rechenproblems durch wiederholte Anwendung desselben Rechenverfahrens schrittweise anzunähern (sukzessive Approximation). Typische Beispiele hierfür sind das Newton-Verfahren zur Berechnung der Nullstellen einer Funktion und die Simpson-Regel zur numerischen Integralberechnung.
Auch hier werden die Ergebnisse eines Schrittes als Ausgangswerte für den jeweils nächsten Schritt genommen. Die Folge der Ergebnisse muss konvergieren. Jedoch ist die Anzahl auszuführender Iterationen nicht vorgegeben: es wird vielmehr solange iteriert, bis entweder eine Abbruchbedingung erfüllt ist oder die Maximalzahl von Iterationen erreicht ist.
Für ein Verfahren P mit seinen Iterationen pi werden daher folgende Größen vorgegeben:
- Maximalzahl für Iterationen i max
- gewünschte maximale Abweichung (Fehler) ε
- Abbruchbedingung - üblicherweise | pi – pi-1 | < ε
Das Verfahren wird somit beendet, wenn die Abbruchbedingung erfüllt ist (z.B. falls die Differenz zum vorangegangenen Rechenschritt kleiner als ε ist) und somit das Ergebnis hinreichend genau bestimmt ist oder die Maximalzahl an Iterationen i max erreicht ist.
Als Beispiel diene wieder die Summe aller Zahlen 0, 1, 2, ... Nun soll jedoch bestimmt werden, ab welchem Iterationsschritt diese Summe einen bestimmten Wert "limit" überschreitet (z.B. limit = 1000). Die Abbruchbedingung lautet folglich sum > limit.
Das Ergebnis dieser Summe und der zugehörige Iterationsschritt sollen als sumfinal und i final zur Verfügung stehen.
Die Umsetzung in Graphing Calculator 3D ist jetzt schon etwas aufwendiger und ein wenig "trickreich" und erfordert neben der Rekursion für die Summenbildung noch zwei weitere Rekursionen, um das Ergebnis sumfinal und den Schritt, bei der die Abbruchbedingung erfüllt ist, i final zu bestimmen:
Iteration mit Abbruchbedingung:
limit = 1000
i max = 2000
i = 1
sum = 0
do while i <= i max
sum = sum + i
if sum > limit then exit do
i = i + 1
loop
sum final = sum
i final = i
Rekursive Lösung mit GC3D:
Als weiteres und typisches Beispiel für die Numerische Mathematik soll die Zahl π bestimmt werden. Hierzu findet man im Web eine große Anzahl an Näherungsverfahren, z.B. bei [1]. Ich habe mich für eine Variante entschieden, bei der Euler zeigen konnte, dass folgende Beziehung gilt (Wert der Zeta-Funktion ζ (4), [2]):
Für die Iteration gilt somit die Abbruchbedingung
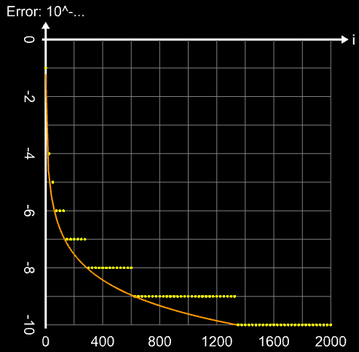
Wie die Grafik zeigt, konvergiert die Iteration "recht zügig", so dass nach 1341 Iterationen π auf 10
Dezimalstellen genau bestimmt ist:
Im nächsten Beispiel soll die Euler'sche Zahl e berechnet werden:
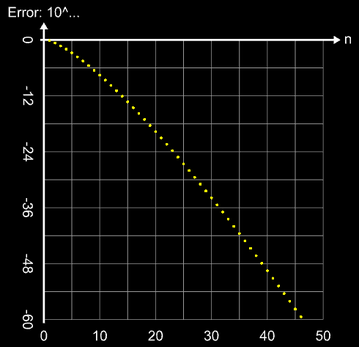
Die Iteration soll beendet werden, falls die Differenz der Ergebnisses vom i-ten zum (i-1)-ten Schritt kleiner als 10-50 ist und somit gilt: fi – fi-1 < 10-50.
Die Reihe konvergiert recht schnell und liefert nach 42 Schritten das gewünschte Ergebnis für e mit 50-stelliger Genauigkeit: e = 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995...
Um mit dieser hohen Genauigkeit zu rechnen, muss man beim Graphing Calculator 3D statt der Standardbibliothek Double die mathematische Bibiliothek Apfloat wählen und die Zahl der Digits (Nachkommastellen) entsprechend groß einstellen (im Beispiel: 60), womit sich jedoch die Rechendauer erhöht.
