Ostrowski-Verfahren

Ostrowski  ging seinerzeit [1] das Problem der Berechnung einer Nullstelle für eine nichtlineare Funktion auf eine neue Weise an: Während das etablierte Sekanten- und Newton-Verfahren in jedem Iterationsschritt eine einzige Verfeinerung bei der Näherung an die Nullstelle durchführen, bestand Ostrowskis neuartiger Ansatz darin, einen Zwischenschritt ("Vorhersage", engl. predictor) für die Nullstelle zu berechnen und diese am Ende jedes Iterationsschrittes weiter zu verbessern (engl. corrector).

In den letzten beiden Dekaden ist diese Zwei- oder Mehrstufigkeit kennzeichnend bei der Entwicklung weiterer Verfahren mit dem Ziel einer höheren Konvergenzordnung (s.u. bei Varianten und bei Diverse Verfahren).

Das zweistufige Ostrowski-Verfahren verwendet die folgenden zwei Gleichungen:

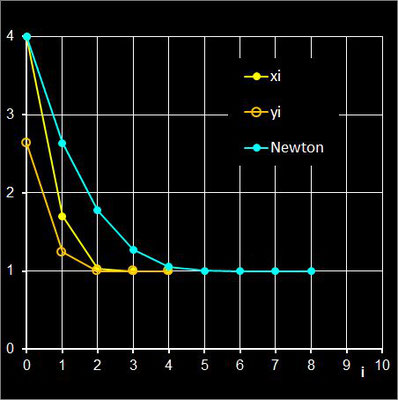
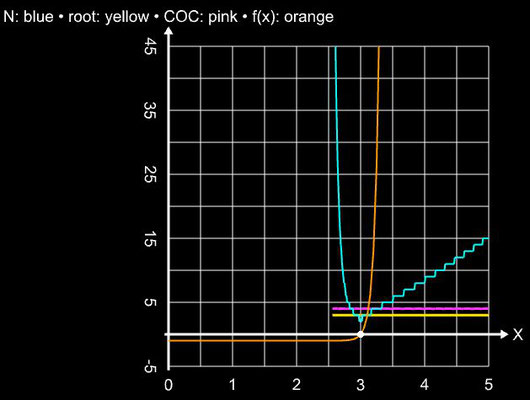
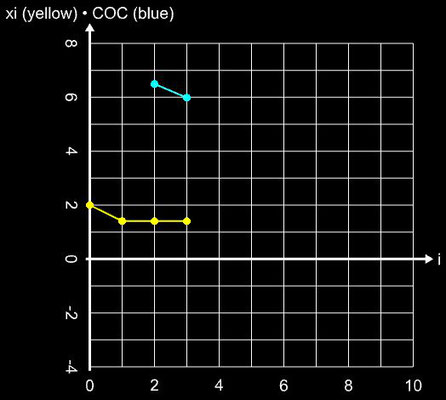
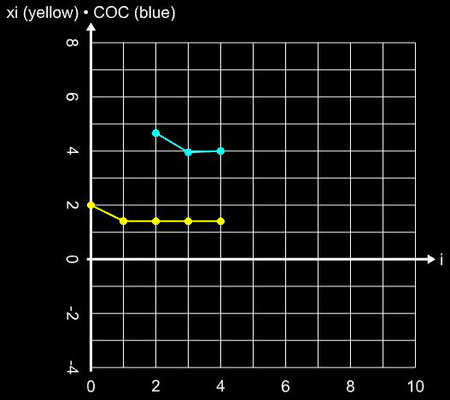
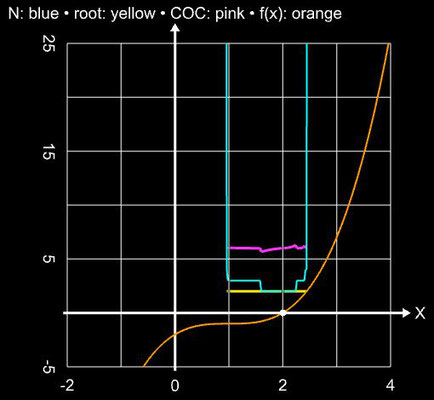
Die erste Gleichung (Predictor) wendet den Newton-Algorithmus an; mittels der zweiten Gleichung (Corrector) wird der vom Predictor erzeugte Zwischenwert y_i weiter verbessert. Die folgende Grafik zeigt am Beispiel der Funktion f (x) = (x + 1)² (x-1) mit der Nullstelle ξ = 1 für x₀ = 4 das Konvergenzverhalten des zweistufigen Ostrowski-Verfahrens mit Predictor y_i (orange) und Corrector x_i (gelb) im Vergleich zum einstufigen Newton-Verfahren (cyan).

Das Ostrowski-Verfahren hat die Konvergenzordnung q = 4. Im Vergleich zum Newton-Verfahren wird eine zusätzliche Funktionsberechnung für f (y_i) benötigt, woraus sich eine Effizienz von CE = 1.587 ergibt.

Als Beispiel für die Anwendung des Verfahrens sowie für seine Varianten (s. weiter unten) diene die Funktion f (x) = sin ² (x) - x² + 1 mit ihren beiden Nullstellen ξ₀ ≈ -1.404491648215341226 und
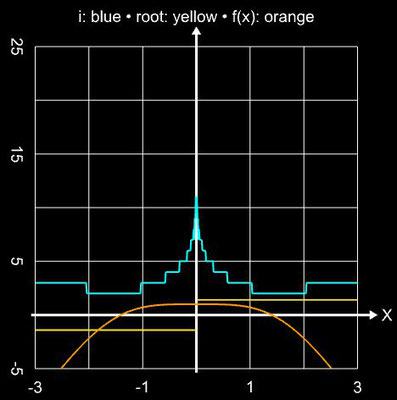
ξ₁ ≈ 1.404491648215341226. Für die schrittweise Darstellung der Iteration wurde x₀ = 2 gesetzt, für den Einzugsbereich wurde das Intervall [-3, 3] (Schrittweite 100) verwendet. Für beide Darstellungen wurde die maximale Anzahl an Iterationen i_max auf 25 begrenzt und als Abbruchkriterium | x_i – x_i-1 | + | f(x_i) | ≤ 10^-15 gewählt.

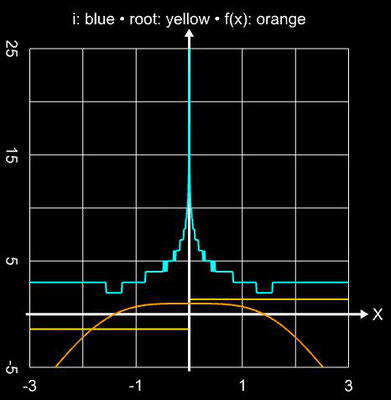
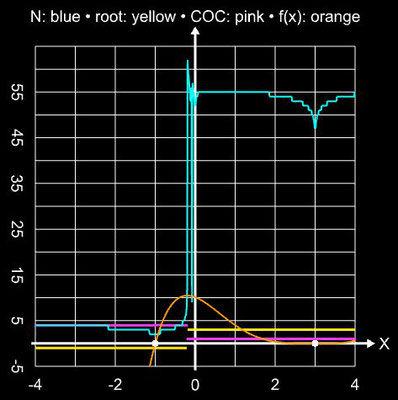
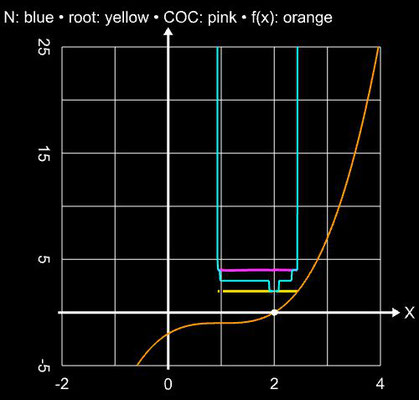
Hier zwei weitere Beispiele für die Anwendung des Verfahrens auf Funktionen mit einfachen Nullstellen: die Funktion f (x) = (x-1)³ - 1 hat eine solche bei ξ = 2 (s. folgende linke Grafik), die Funktion e^x²+7x-30 - 1 besitzt für x ≥ 0 die Nullstelle ξ = 3. Der Einzugsbereich ist ähnlich dem Newton-Verfahren, kommt aber nicht ansatzweise an den des Tiruheh-Verfahrens heran (s. Beispiele unter Konvergenzbetrachtungen beim Tiruneh-Verfahren).

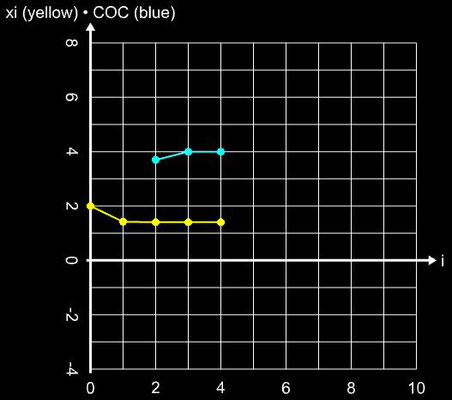
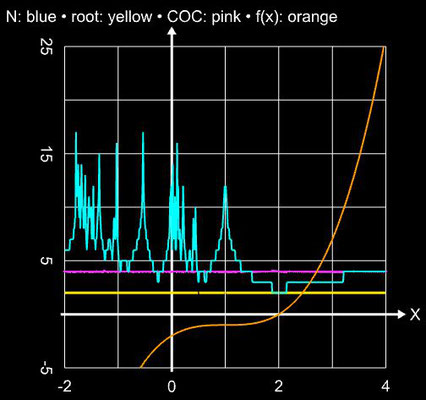
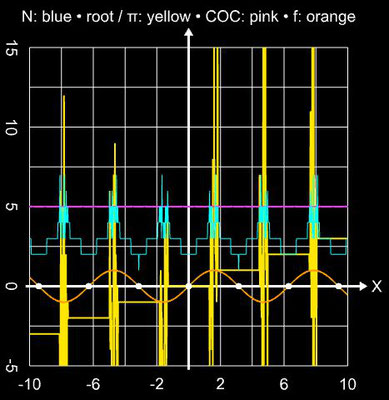
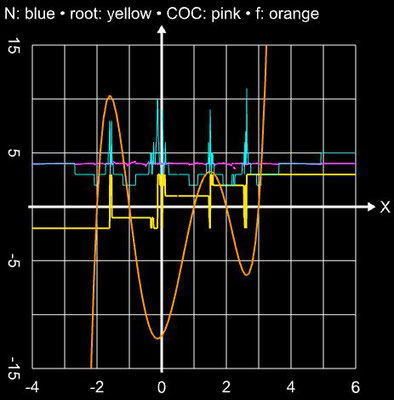
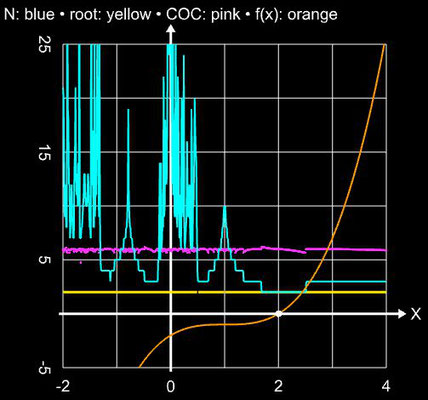
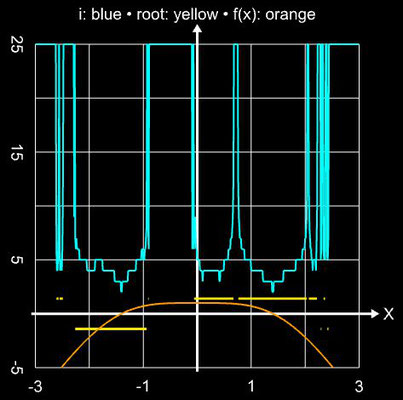
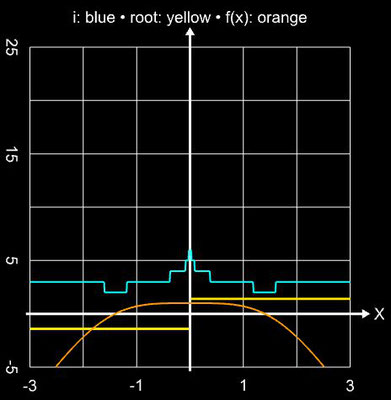
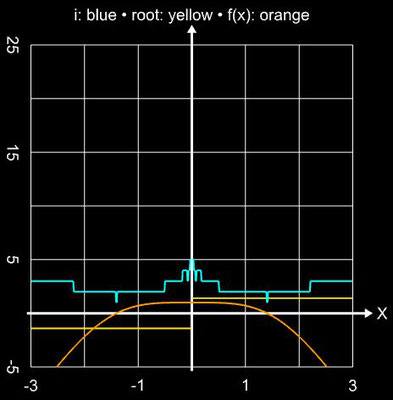
Angewandt auf die Funktion f (x) = sin (x) und das Polynom f (x) = x⁵ - 3x⁴ - 5x³ + 15x² + 4x - 12  liefert das Verfahren in einer hinreichend kleinen Umgebung der Nullstellen stabil das Ergebnis (waagerechte Linien in den folgenden beiden Diagrammen), während es im Bereich um Extremwerte zu Sprüngen zwischen den Lösungen kommt (vgl. mit Newton-Verfahren):

Im Fall der Funktion f (x) = sin (x) ist der COC-Wert mit ca. 5 sogar höher als der theoretische Wert von q = 4.

Liegt bei einer Funktion eine mehrfache Nullstelle vor, sinkt die Konvergenzordnung des Verfahrens auf den Wert q = 1, wie es im folgenden Beispiel für die Funktion f (x) = 0.125 (x+1) (x-3)⁴ mit der einfachen Nullstelle ξ₁ = -1, der vierfachen Nullstelle ξ₂ = 3 und dem Abbruchkriterium | x_i – x_i-1 | + | f(x_i) | ≤ 10^-15 zu sehen ist.

Grau und Diaz-Barrero optimierten das Verfahren von Ostrowski hinsichtlich der Konvergenzordnung gemäß folgender Iterationsvorschrift [2] :

Das Verfahren hat nun die Konvergenzordnung q = 6 bei einer Effizienz CE = 1.565. Angewandt auf die Beispielfunktion (s.o.), ergibt sich folgendes Ergebnis:

Im nächsten Bild wurde die Variante von Grau/Diaz-Barrero auf die Funktion f (x) = (x-1)³ - 1 mit ihrer einfachen Nullstelle bei ξ = 2 angewandt (vgl. mit obigem Ergebnis beim ursprünglichen Ostrowski-Verfahren).

Um eine Version des Ostrwoski-Verfahrens ohne Ableitung zu erhalten, kann diese durch den Vorwärts-Differenzenquotient

ersetzt werden. Somit ergibt sich ein weiteres Verfahren:

dessen Konvergenzordnung dann aber nur q = 3 beträgt. Angewandt auf die Beispielfunktion zeigt sich ein deutlich reduzierter, lückenhafter EInzugsbereich:

Cordero et al. [3] approximieren hingegen die Ableitung durch den Zentralen Differenzenquotient

womit sich das folgende Verfahren ergibt

mit einer Konvergenzordnung q = 4.

Die ableitungsfreie Variante von Cordero et al. wurde ebenfalls auf die Funktion f (x) = (x-1)³ - 1 mit ihrer einfachen Nullstelle bei ξ = 2 angewandt (s. folgendes Bild). Gegenüber dem ursprünglichen Ostrowski-Verfahren (s.o.) ist der Einzugsbereich nun stark eingeschränkt.

Auch beim von Grau und Diaz-Barrero optimierten Ostrowski-Verfahren [2] approximieren Cordero et al. in [3] die Ableitung durch den zentralen Differenzenquotienten und erhalten somit ein ableitungsfreies Verfahren:

das ebenfalls die Konvergenzordnung q = 6 bei einer Effizien CE = 1.431 besitzt.

Angewandt auf die Funktion f (x) = (x-1)³ - 1 mit ihrer einfachen Nullstelle bei ξ = 2 zeigt das Verfahren gegenüber dem ursprünglichen Ostrowski-Verfahren (s.o.) einen stark eingeschränkten Einzugsbereich:

Quellenverweise

[1]   A.M. Ostrowski, Solutions of Equations and Systems of Equations, Academic Press, New York, 1960

[2]   M. Grau, J.L. Diaz-Barrero, An improvement to Ostrowski root-finding method, 
       Appl. Math. Comput. 173  (2006) 450–456

[3]   A. Cordero et al., Steffensen type methods for solving nonlinear equations,
      Journal of Computational and Applied Mathematics, Vol. 236, Issue 12 (2012) 3058-3064