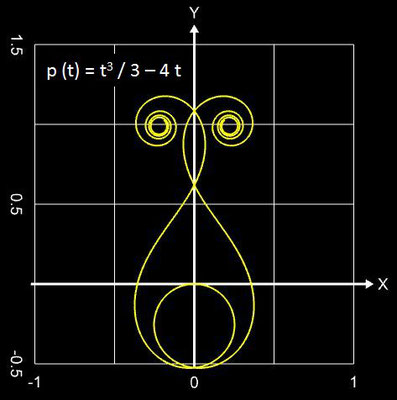
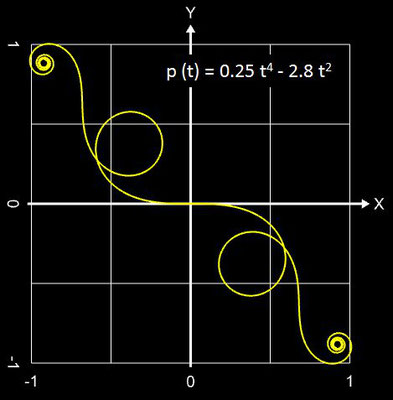
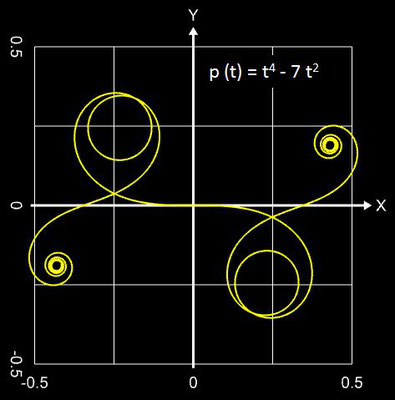
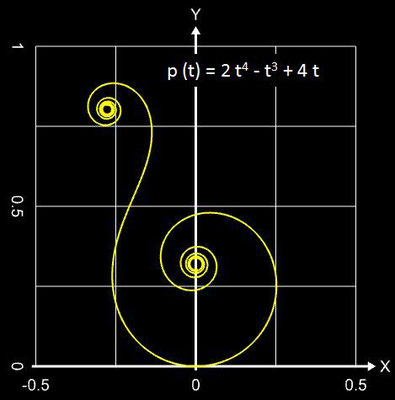
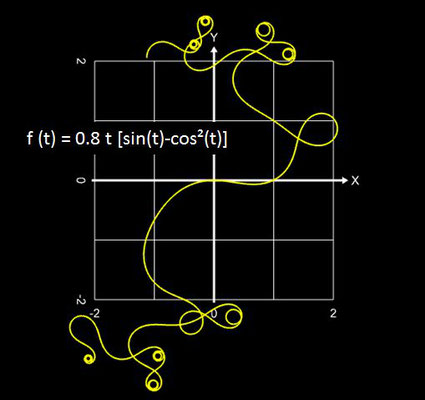
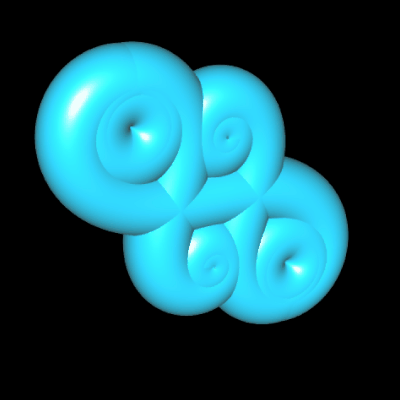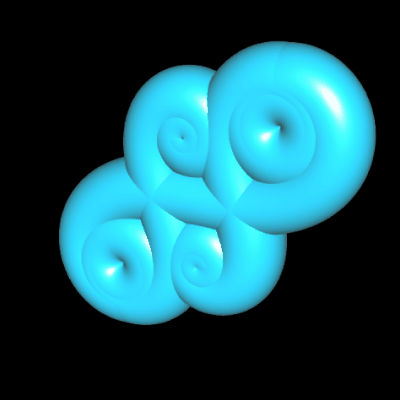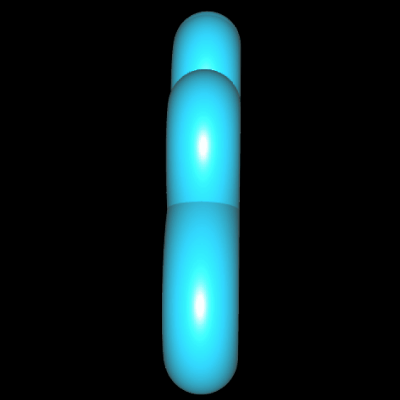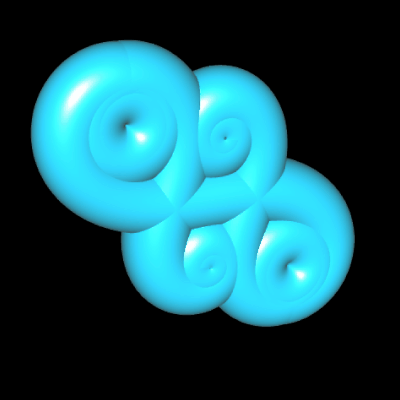Polynomiale Spirale
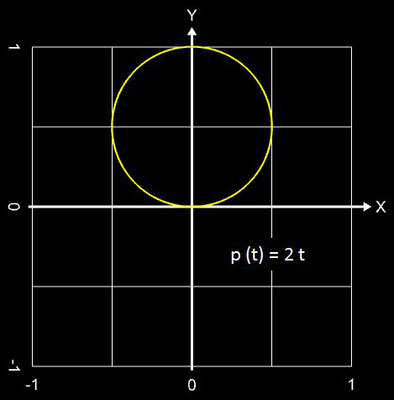
Ersetzt man die krümmungsrelevanten Argumente der Sinus- und Cosinusfunktion in den Integralen der Gleichungen einer Klothoide (Cornu-Spirale) durch ein Polynom
so erhält man die polynomiale Spirale [1], [2]:
Die Krümmung dieser Spirale beträgt dann
Die polynomialen Spiralen bilden eine eigene Klasse, bei denen die Krümmung κ ein Polynom der Bogenlänge ist; ihre Eigenschaften wurden in [3] untersucht.
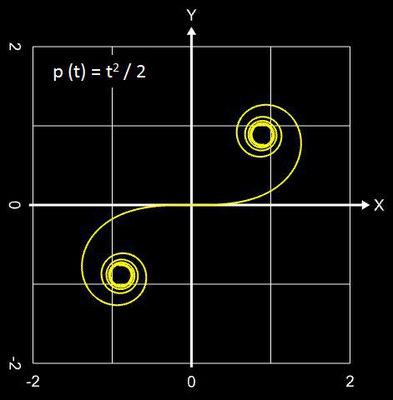
Mithin ist die Einheitsklothoide mit p (t) = t² / 2 ein Spezialfall der polynomialen Spirale. Einige Beispiele polynomialer Spiralen zeigen die folgenden Abbildungen.
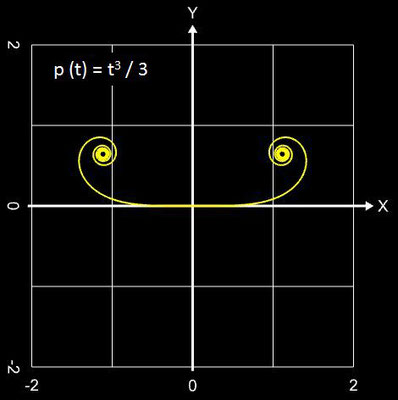
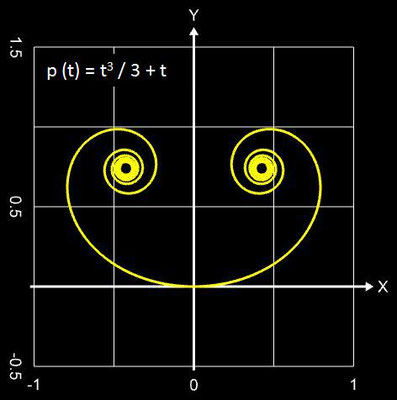
Falls in p (t) nur gerade Exponenten vorkommen, sind beide Äste der Spirale punktsymmetrisch zum Ursprung (0 | 0); kommen nur ungerade Exponenten vor, so sind beide Äste achsensymmetrisch. Bei gemischt vorkommenden Exponenten liegt keine Symmetrie vor, die beiden Äste sind unterschiedlich geformt (vgl. mit obiger Galerie).
Polynomiale Spirale als Rohr/Röhre
Die polynomiale Spirale kann auch als Rohr/Röhre dargestellt werden. Im folgenden dazu drei Beispiele mit (von links nnach rechts)
p (t) = t3 + t ,
p (t) = t4 – 4.6 t2 sowie
p (t) = 0.25 t4 – 2.8 t2. Wie dies mathematisch umgesetzt ist sowie weitere Beispiele "ummantelter" polynomialer Spiralen finden Sie unter Funktionsgraph als Rohr/Röhre.
Interessante Objekte entstehen, wenn man den Kreis als Querschnitt durch eine andere Kurve ersetzt (z.B. Astroide, vgl. Funktionsgraph als Rohr/Röhre), den Radius des Querschnitts groß wählt oder Beides miteinander kombiniert. Im folgenden wurde dies für die letzte Spirale in der vorigen Galerie umgesetzt.
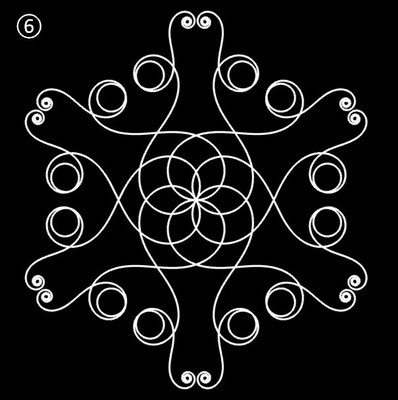
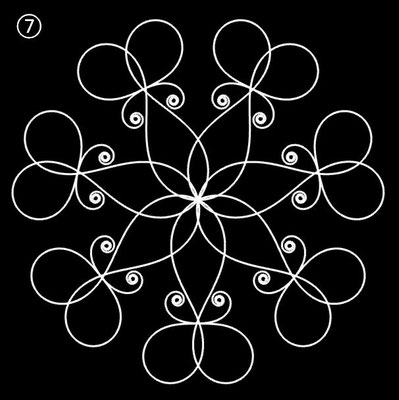
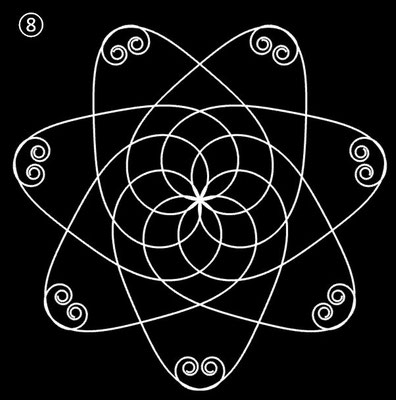
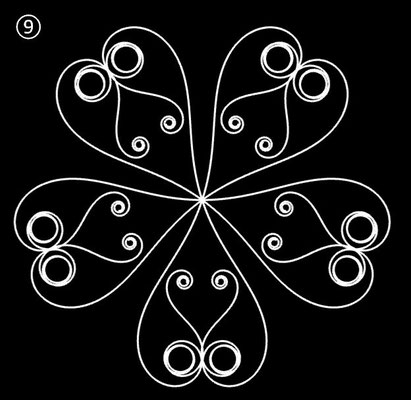
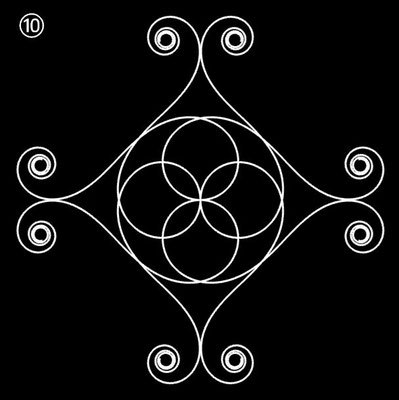
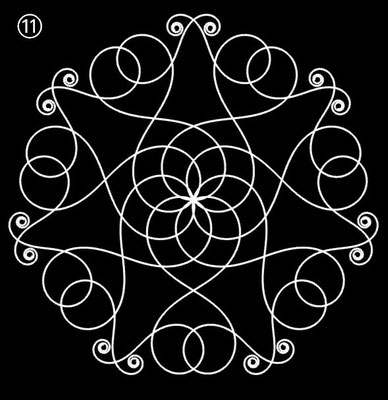
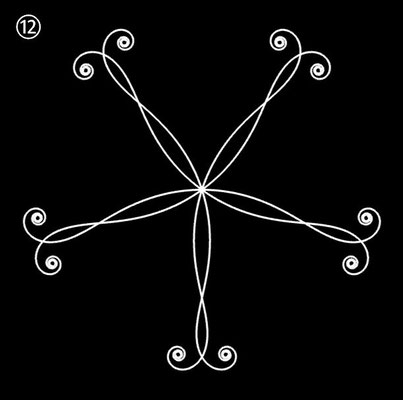
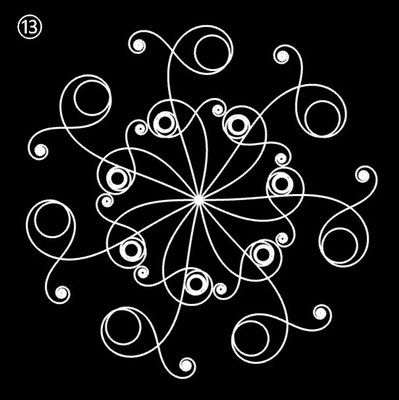
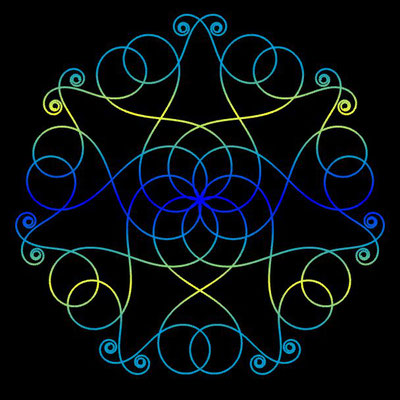
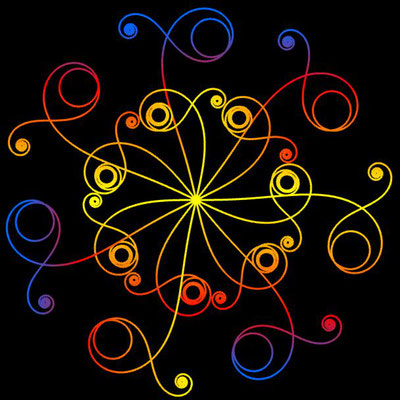
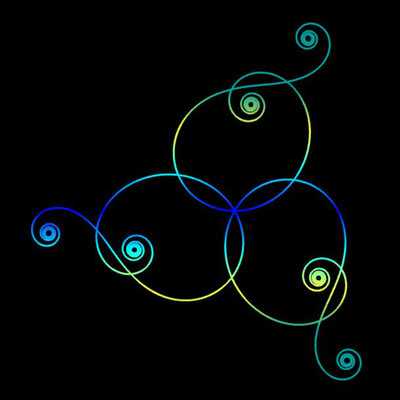
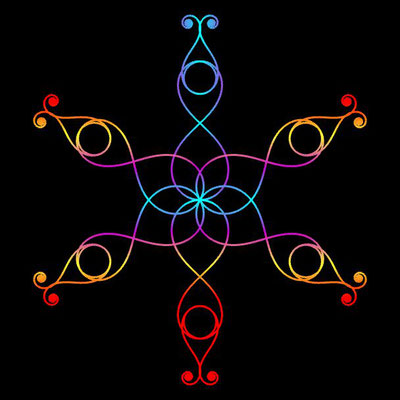
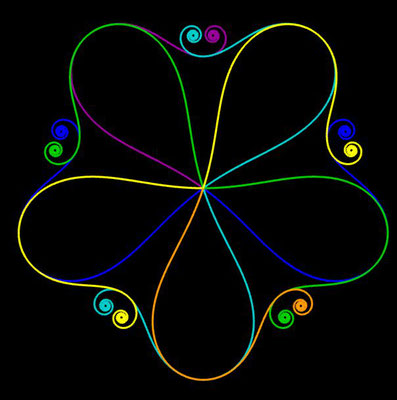
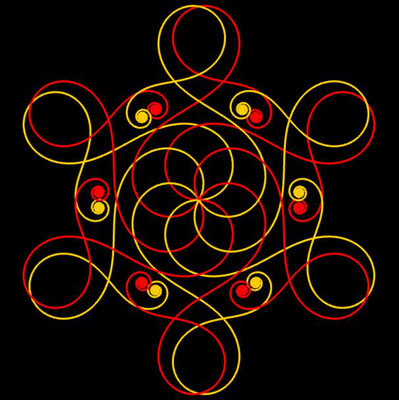
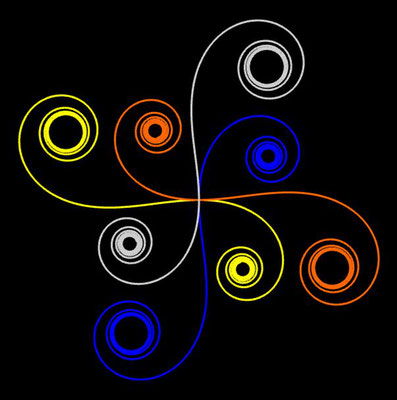
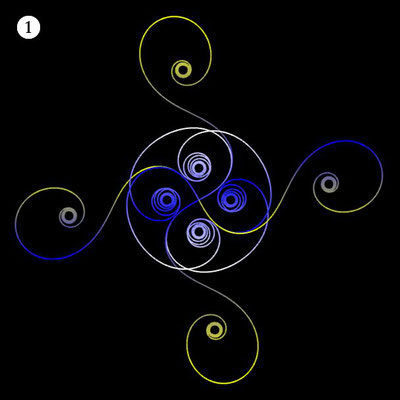
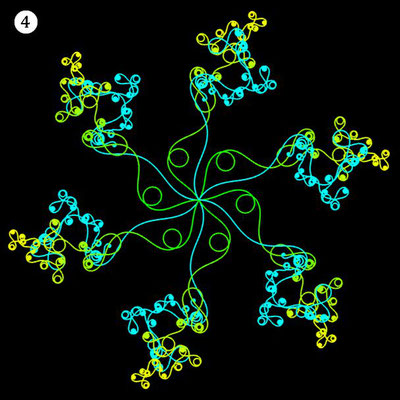
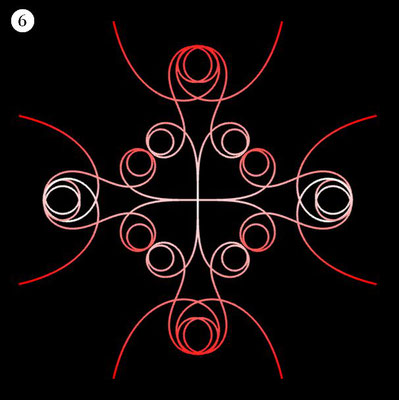
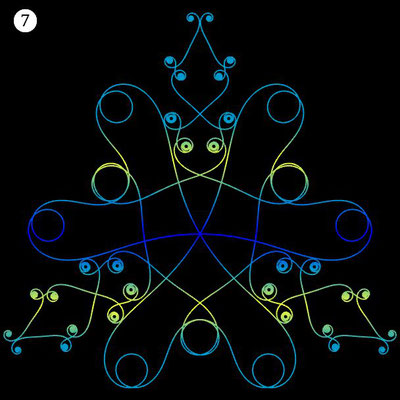
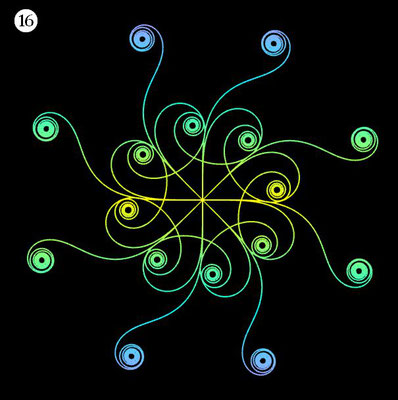
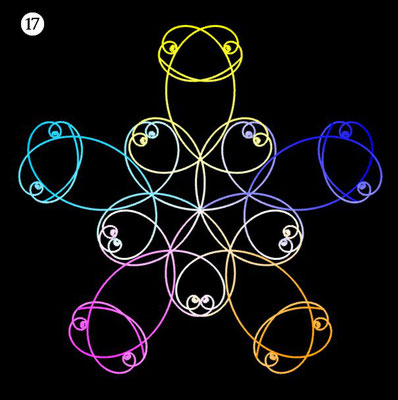
Ornamente aus polynomialen Spiralen

Im Folgenden soll der ästhetische Aspekt der polynomialen Spirale im Vordergrund stehen.
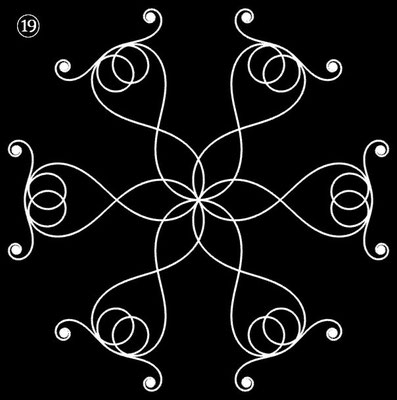
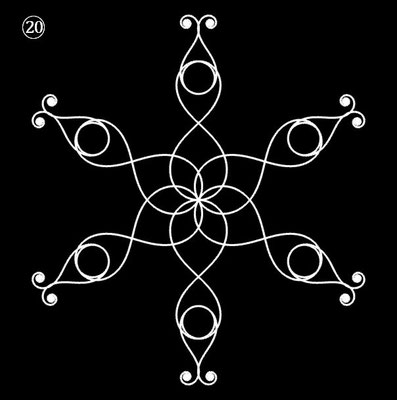
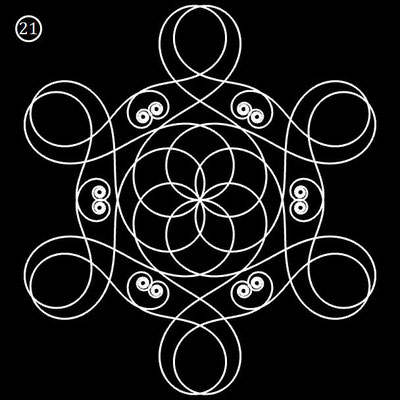
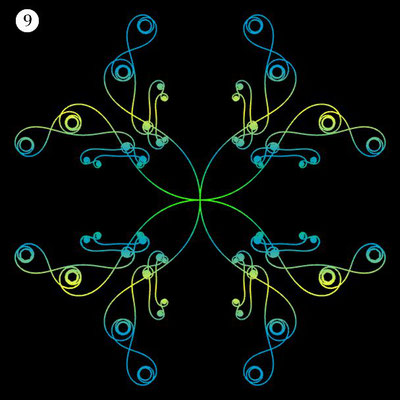
Interessanterweise findet man z.B. bei schmiedeeisernen Toren, Fenstergittern, Geländern und Zäunen sehr oft Dekorationen, die Elemente der obigen Spiralen enthalten. Auf Grund ihrer Verschnörkelungen aber auch Symmetrie eignen sich polynomiale Spiralen idealerweise zur Konstruktion von Ornamenten, bestehend aus w Einzelspiralen.
Hierzu werden, ausgehend von einer Ursprungsspirale mit einem Startwinkel θ0 = 0, weitere Clones gebildet, die jeweils um einen Winkel 2π / w weitergedreht werden, d.h. es sind w polynomiale Spiralen zu berechnen mit
Da bei hinreichender Auflösung die Berechnung der Integrale zeitintensiv ist - bei meinem derzeitigen PC (s. Tools) um die 10 Sekunden für eine einzige Spirale - habe ich die "alternative Parametrisierung" der Klothoide (s. unten bei Klothoide (Cornu-Spirale) für die polynomiale Spirale adaptiert:
mit i = 0, …, N-1 und
x0 = 0, y0 = 0.
Wichtig ist hierbei die Wahl eines hinreichend großen Wertes für N (s. dazu den Abschnitt Klothoide mit alternativer Parametrisierung unter Klothoide). Bei den für die Ornamente verwendeten Werten für L reicht ein Wert von N = 5000 aus. Für die Länge des positiven und negativen Astes können auch unterschiedliche Werte verwendet werden.
Durch Anwendung des obigen Verfahrens liegt die Rechenzeit z.B. für ein Ornament aus 8 polynomialen Spiralen unter einer (!) Sekunde. Dies eröffnet einem die Möglichkeit, bei nahezu gleichzeitiger Anzeige des Ergebnisses, mit verschiedenen Polynomen und Werten für L zu experimentieren. Mit Hilfe des Parameters a (0 < a) lassen sich die Spiralen nochmals auf schnelle Weise ändern, teils mit verblüffenden Ergebnissen. Zum eigenen Experimentieren finden Sie im Download-Bereich eine Datei für den Graphing Calculator 3D.
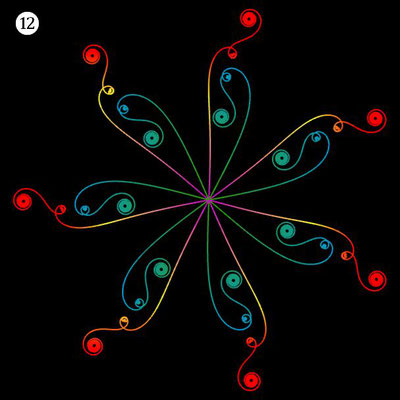
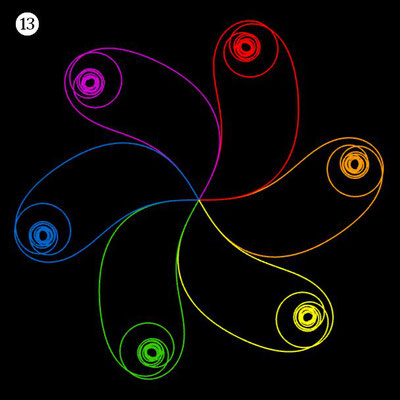
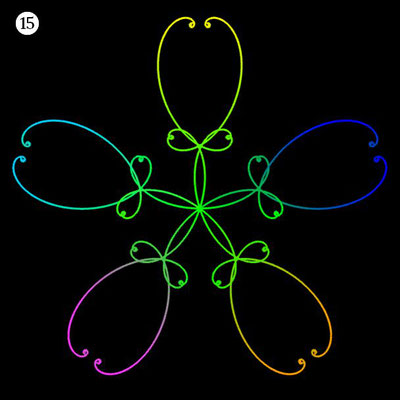
Die folgende Galerie zeigt eine Auswahl an Ornamenten aus polynomialen Spiralen. Bei der Zusammenstellung der Galerie gab es, wie auch z.B. bei den Spherical Harmonics, 2D
Superformeln und 3D Supershapes die Qual der Wahl. So können durch Verändern nur eines
Faktors bei einem Polynom vollkommen andersartige Objekte entstehen. Dies ist z.B. bei den Ornamenten ③,
⑤, ⑨, ⑪, ⑰ bis ⑳
der Fall, bei denen nur der Faktor des linearen Anteils beim Polynom
t5 - 6
t3 + ... t verändert wurde.
Die in der Galerie verwendeten Polynome und Parameter finden Sie in der Tabelle am Ende der Seite.
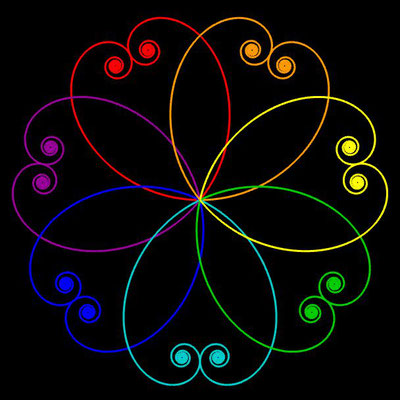
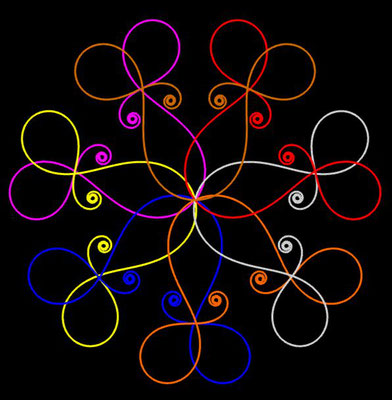
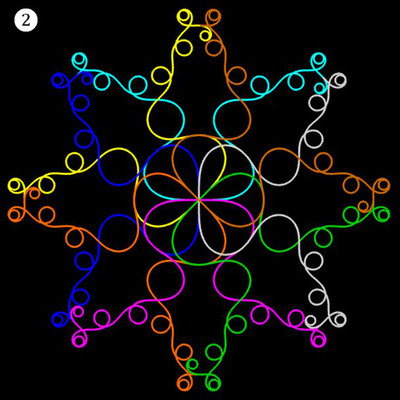
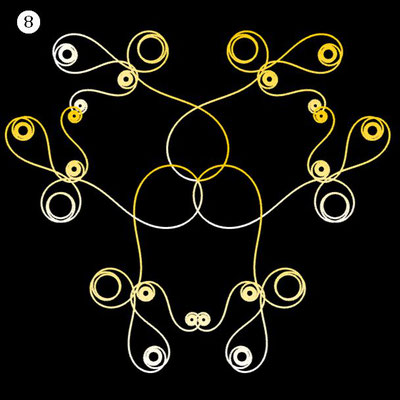
Noch einen Tick ansprechender präsentieren sich die obigen Ornamente, wenn man diese einfärbt, sei es mit unterschiedlichen Farben für die einzelnen polynomialen Spiralen oder durch Farbverläufe. In der folgenden Galerie finden Sie hierzu eine kleine Auswahl ... wie gesagt: die Qual der Wahl ...
Interessante dreidimensionale Ornamente ergeben sich, wenn man die polynomialen Spiralen als Rohr/Röhre darstellt (s. oben sowie unter Funktionsgraph als Rohr/Röhre). Die für die folgenden drei Beispiele zugrunde liegenden Polynome sind (von links nach rechts)
- p (t) = t4 - 4 t2 w = 5
- p (t) = t4 - 7 t w = 4
- p (t) = t4 - 6.1 t w = 4.
Beim letzten Ornament wurde der Querschnitt mit einer Astroide erzeugt (s. oben), um den Eindruck einer schmiedeeisernern Arbeit zu erwecken - eine echte Herausforderung für einen Kunstschmied ... ;-)
Die schon unendliche Formenvielfalt der polynomialen Spirale lässt sich nochmals erweitern, indem an Stelle des Polynoms eine beliebige (stetig differenzierbare) Funktion f verwendet wird:
Auch hier kann die obige Parametrisierung anstelle der zeitintensiven Berechnung mit Integralen verwendet werden, indem p (t) durch f (t) ersetzt wird.
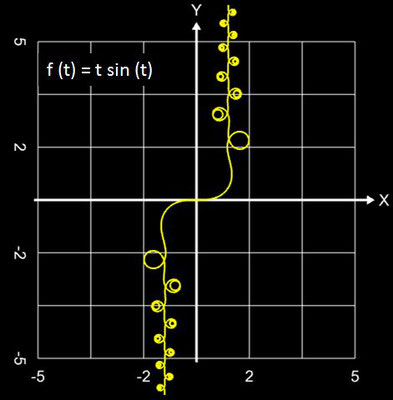
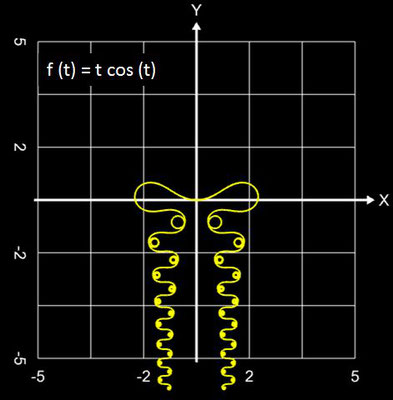
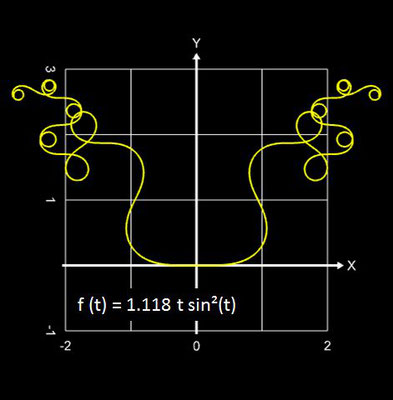
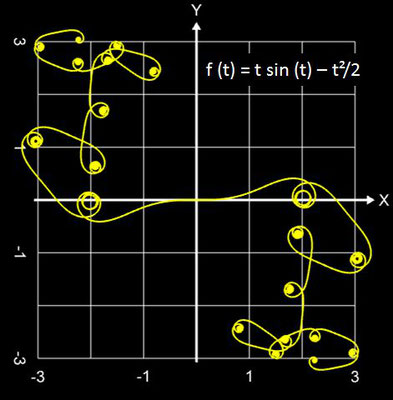
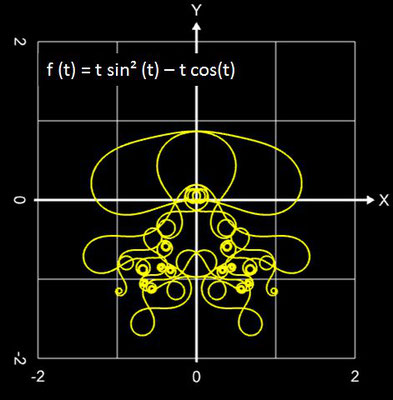
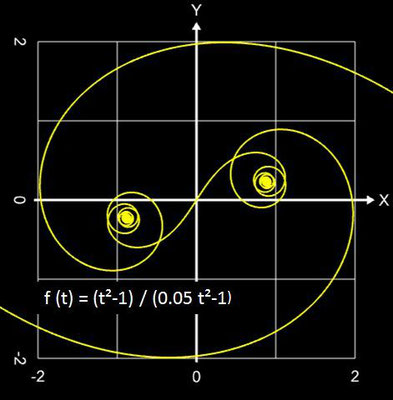
Es ist recht schwierig, beim Blick auf die Funktion f (t) das Aussehen des entstehenden Graphs vorherzusagen. Um dem Kind einen Namen zu geben, nenne ich diesen Graph "funktionale Spirale", wenngleich dies auch etwas vage ist, denn
- bei der polynomialen Spirale endet der Graph für große Werte von L stets in einer Spirale,
- enthält f (t) aber z.B. Terme der Form tn sinm(t) oder tn cosm(t), so entstehen jedoch Linien/Ketten mit vielen kleinen Spiralen, Kringeln und Schnörkeln, die sich ins Unendliche fortsetzen.
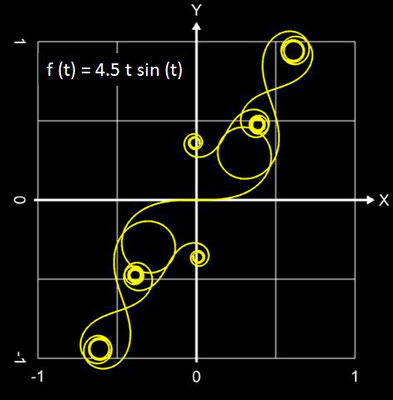
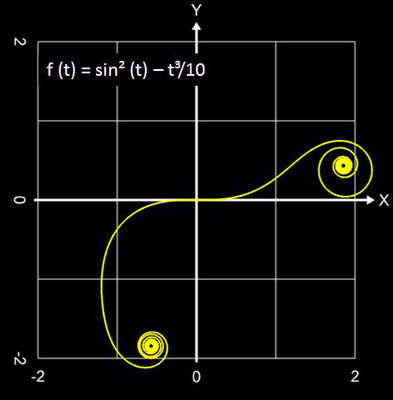
Hier einige Beispiele "funktionaler Spiralen" ...
Die folgende Galerie zeigt einige Ornamente, die mit "funktionalen Spiralen" erzeugt wurden.
Ornamente aus Spiralen - Tabelle der verwendeten Polynome / Funktionen und Parameter
| Ornam. | Polynom p (t) | w | L+ | L- | a |
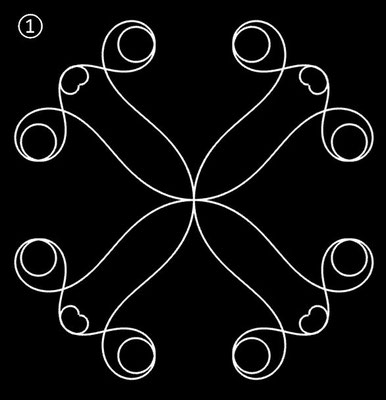
| ① | t5 - 6.1 t3 + 3.1 t | 4 | ± 2.22 | 1 | |
| ② | t5 - 6.2 t3 + 3.1 t | 4 | ± 2.22 | 4.0322 | |
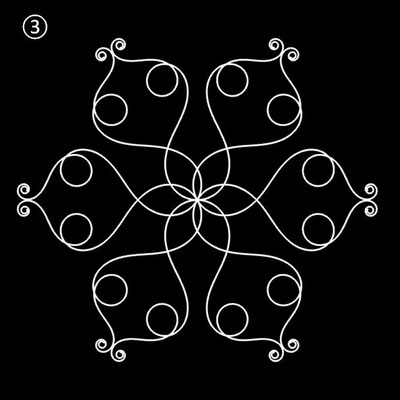
| ③ | t5 - 6 t3 + 5.4 t | 6 | ± ¾ π | 1 | |
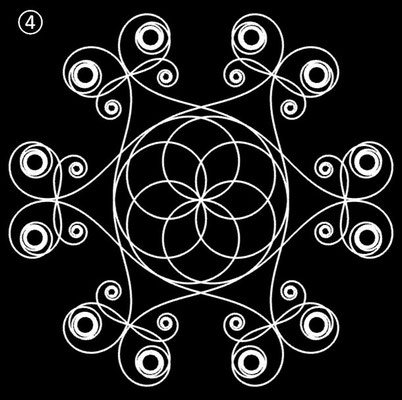
| ④ | t5 - 6.2 t3 + 3.38 t | 6 | ± 2.22 | 4.0322 | |
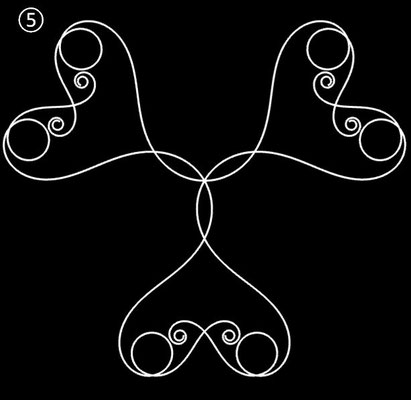
| ⑤ | t5 - 6 t3 + 4.32 t | 3 | ± ¾ π | 1 | |
| ⑥ | t5 - 6 t3 + 5.4 t | 6 | ± ¾ π | 1.59 | |
| ⑦ | t5 - 5.115 t3 + 4.35 t | 7 | ± ¾ π | 1 | |
| ⑧ | 2.4 t5 - 6 t3 + 7 t | 7 | ± 1.73 | 1 | |
| ⑨ | t5 - 6 t3 + t | 5 | ± ¾ π | 1.59 | |
| ⑩ | t3 - 3.275 t | 4 | ± 1.5 π | 1 | |
| ⑪ | t5 - 6 t3 + 7.02 t | 7 | ± 2.4 | 1 | |
| ⑫ | t5 - t | 5 | ± 3/5 π | 1 | |
| ⑬ | 2 t5 - 10.565 t3 + 4 t2 | 7 | ± 2.4 | 1 | |
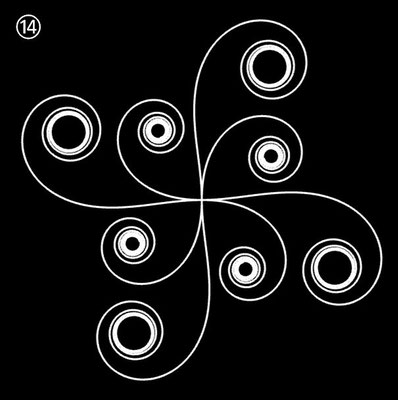
| ⑭ | t3 - 8 t2 + 2 t | 4 | 3 | -2 | 1 |
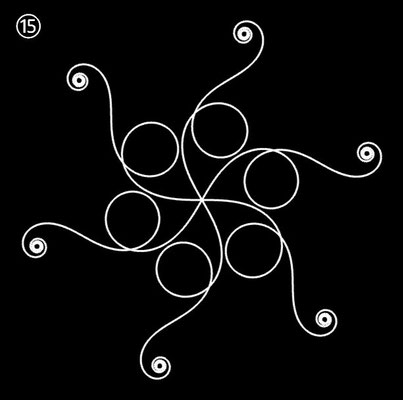
| ⑮ | 0.25 t4 - 2.8 t2 | 3 | ± 4 | 1 | |
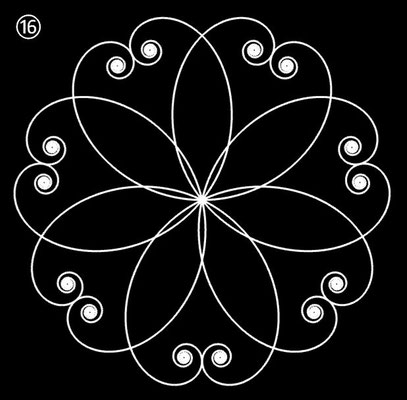
| ⑯ | 2 t5 - 0.5 t3 + 1.95 t | 7 | ± 2 | 1 | |
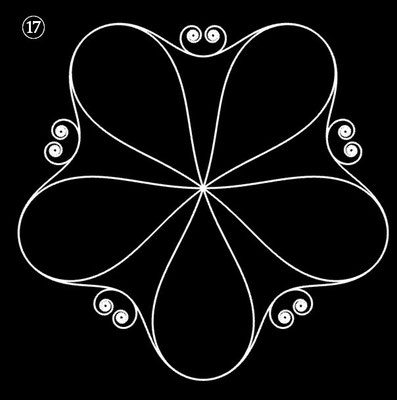
| ⑰ | 2.45 t5 - 6 t3 + t | 5 | ± 2 | 1 | |
| ⑱ | t5 - 6 t3 + 4 t | 6 | ± 4.5 | 1 | |
| ⑲ | t5 - 6 t3 + 5 t | 6 | ± 4.5 | 1 | |
| ⑳ | t5 - 6 t3 + 6 t | 6 | ± 4.5 | 1 | |
|
|
t5 - 6 t3 + 7.9 t | 6 | ± 2.5 | 1 | |
| Ornam. | Funktion f (t) | w | L+ | L- | a |
| ❶ | t3 / 3 - 2.65 cos5(t) | 4 | ± 5 | 1 | |
|
❷ |
1.5 t sin5(t) | 8 | 9 | -8 | 1 |
|
❸ |
t3 / 3 - 2.7 cos5(t) | 4 | ± 5 | 0.7 | |
|
❹ |
t cos(t) - t2 / 2 | 6 | ± 60 | 1 | |
|
❺ |
10 t2 sin3(t) - 3.5 cos3(t) | 3 | ± 20 | 0.294 | |
|
❻ |
t3 exp(- t2 / 10) | 4 | ± 9 | 1 | |
|
❼ |
10 t2 sin3(t) - 3 cos(t) t | 3 | ± 10 | 0.294 | |
|
❽ |
5 t cos(t) | 3 | ± 12 | 1 | |
|
❾ |
10 t2 sin3(t) - 3 cos(t) t | 4 | ± 10 | 1 | |
| ❿ | 5 t √ | sin(t) | | 3 | ± 12.5 | 0.91 | |
| ⓫ | (4 t5 - 1) / (1.9 t3 - 1) | 6 | 2.45 | -6 | 1 |
| ⓬ | (t5 -1) / ( t2 - 2) | 7 | ± 4 | 1.27 | |
| ⓭ | sin2(t) - t3 / 10 | 6 | ± 7 | 1 | |
| ⓮ | 4.2 t √ | sin(t) | | 5 | ± 12 | 1 | |
|
⓯ |
0.7 tan (2 t) | 5 | ± 2.45 | 1 | |
| ⓰ | t3 / 3 - 2 sin4(t) | 8 | ± 5 | 1.24 | |
| ⓱ | tan (t) | 5 | ± 6 | 1.4 | |
| ⓲ | t2 - 4 tan (t) | 3 | ± 7 | 1 | |
Links
[1] http://www.2dcurves.com/spiral/spiralps.html
[2] http://old.nationalcurvebank.org///waldman4/polynomialspiraland%20beyond.pdf
Download
... auf Anfrage ...