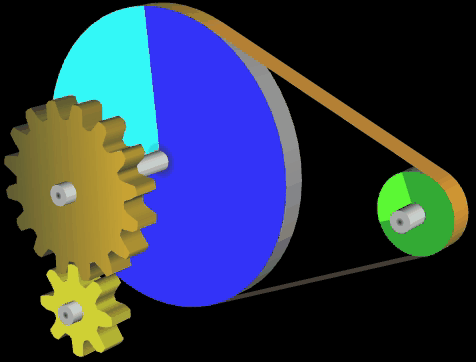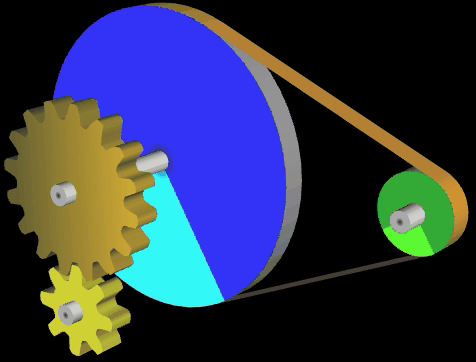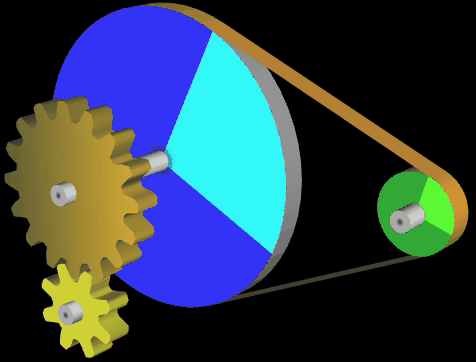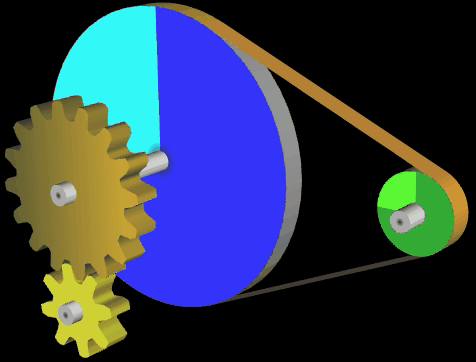
3D Riementrieb (Transmission)
Riementriebe (auch Riemengetriebe, Transmission) dienen zur Übertragung von Drehbewegungen und Drehmomenten. Im Zeitalter der Industrialisierung wurden Riementriebe damals genutzt, um eine zentral erzeugte Antriebsleistung (z.B. Dampfmaschine, Wasserrad) über lange, unterhalb der Decke der Fabrikationshallen laufende Transmissionswellen per Flachriemen (oft aus Leder oder Textil) an die einzelnen Produktions-maschinen abzugeben (s. Grafik unten).
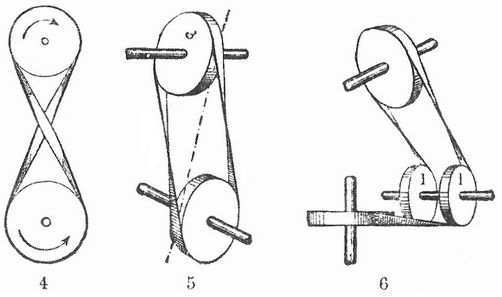
Sogar eine Umkehr der Drehrichtung oder eine Anordnung der Riemen in orthogonal zueinander befindlichen Ebenen konnte realisiert werden. In Meyers Großes Konversationslexikon von 1905 findet sich eine Abbildung mit drei Antriebsszenarien:
Fig. 4 Gekreuzter Riemen, Fig. 5 Geschränkter Riemen, Fig. 6 Riementrieb mit Leitrollen (s. folgende Grafik).
![Riementrieb (Transmission) in alter Mühle [1]](https://image.jimcdn.com/app/cms/image/transf/none/path/scee86bccd27a6ab2/image/i5060d2cc429def6d/version/1583657856/image.jpg)
![Drehbänke in Maschinenbauanstalt (1849) [1]](https://image.jimcdn.com/app/cms/image/transf/dimension=1920x400:format=jpg/path/scee86bccd27a6ab2/image/i14e217550c587f0d/version/1724665458/image.jpg)
Durch die Einführung elektrischer Antriebsmaschinen (Direktantrieb von Werkzeug- / Produktions-maschinen) und auf Grund mehrerer Nachteile der Lederriemen wurde der Riementrieb immer seltener eingesetzt.
Im modernen Maschinenbau sind Riementriebe oftmals genutzte getriebetechnische Lösungen mit Riemen aus diversen Hochleistungswerkstoffen und eingelegten zugverstärkenden Materialien. Ihre Gestaltungs-möglichkeiten sind sehr vielfältig; sie sind oft die einzige Lösung, wenn größere Abstände zu überbrücken sind. Typische Anwendungen des Riementriebs finden sich z.B. im KFZ zum Antrieb der Lichtmaschine, als Verbindung von Kurbel- und Nockenwelle, in Waschmaschinen oder auch als Alternative zu einer Kette beim Fahrrad.
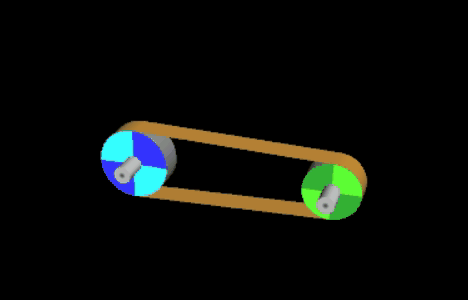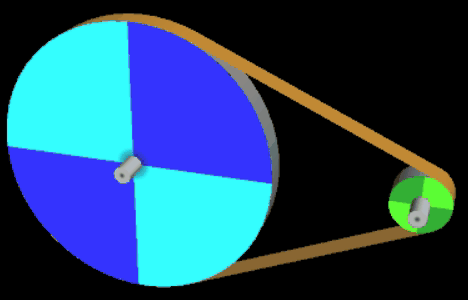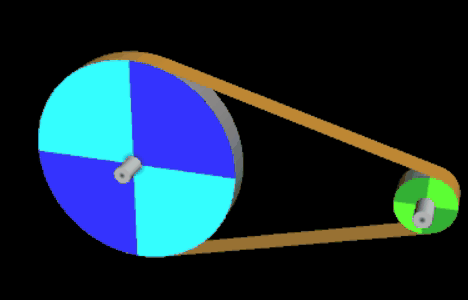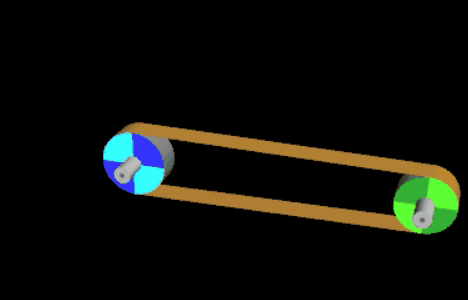
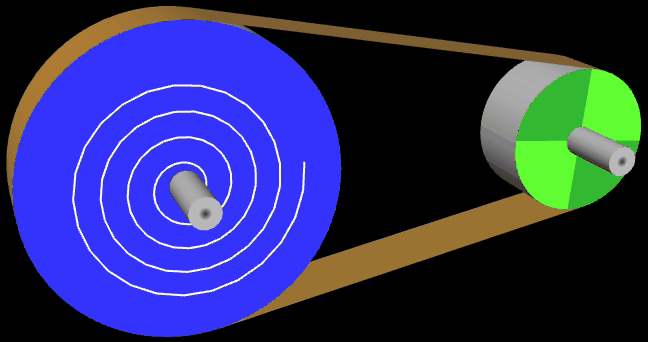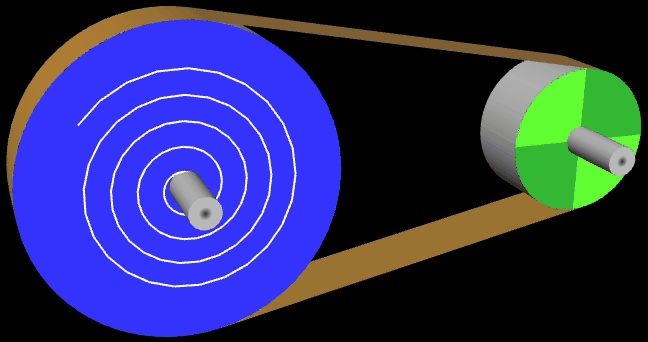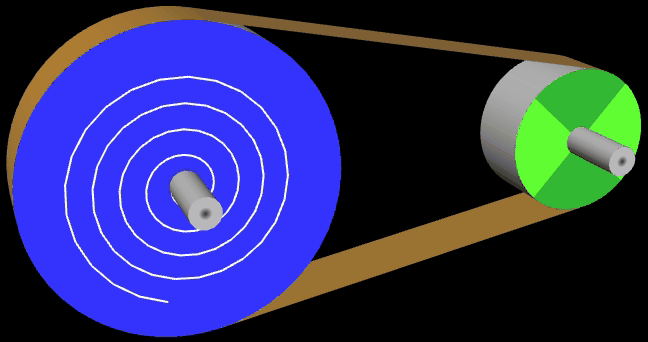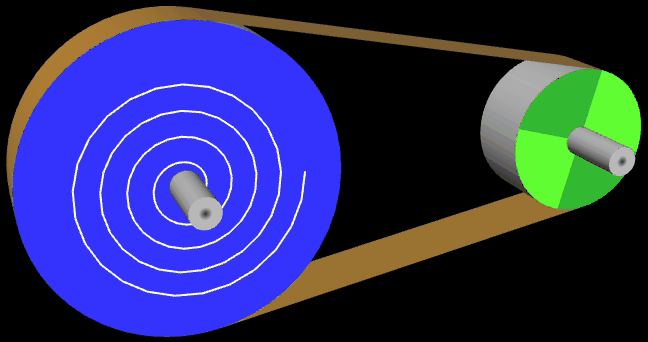
Ein Riementrieb mit Flachriemen soll als Animation dargestellt werden (s.o.). Außerdem soll die erforderliche Länge L des Treibriemens berechnet werden.
Der Riementrieb besteht aus zwei Scheiben mit den Radien r1 und r2 sowie einem Flachriemen. Die Radien sowie der Mittelpunktsabstand D können frei gewählt werden. Die nebenstehende Abbildung zeigt eine typische Konstellation mit den zu bestimmenden Größen. Ohne Bechränkung der Allgemeinheit liegt der Mittelpunkt einer der Scheiben im Ursprung eines Koordinatensystems.
Bei der Animation wird etwas geschummelt, denn die Scheiben drehen sich, der Treibriemen steht jedoch still. Dieser besteht aus zwei gleich langen Strecken der Länge b sowie zwei Kreisbögen b1 und b2 entlang der Scheiben; mithin gilt für seine Länge L der Zusammenhang
L = 2 b + 
+ 
= 2 b + b1 + b2
An den Punkten A und B (bzw. A' und B') geht die Strecke b in die Kreisbögen über. Es sind die Punkte, an denen die Tangente t die beiden Scheiben berührt und die es zu bestimmen gilt. Für die Animation entnimmt man der obigen Grafik die folgenden Zusammenhänge:
Für die Berechnung der Riemenlänge gelten die folgenden Zusammenhänge:
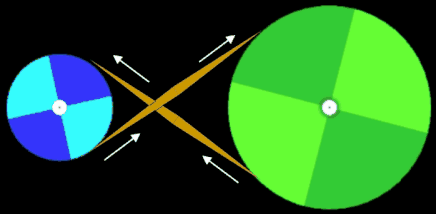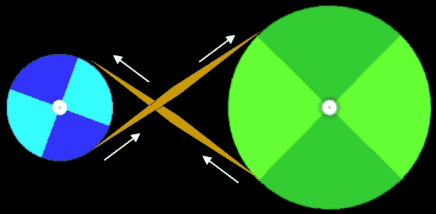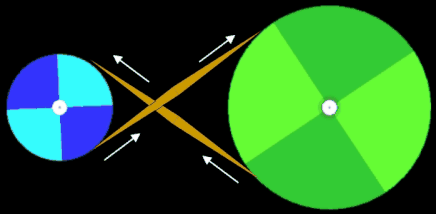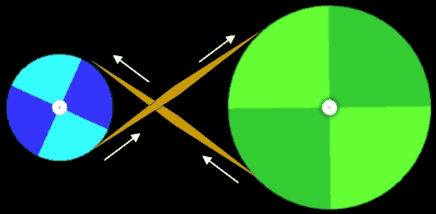
Ein Antriebsszenario mit gekreuztem Riemen und somit einer Richtungs-umkehr der Drehbewegung zeigen die beiden folgenden Grafiken.
Für die Berechnung der Riemenposition und der Berührpunkte siehe
Kreise mit inneren Tangenten verbinden.
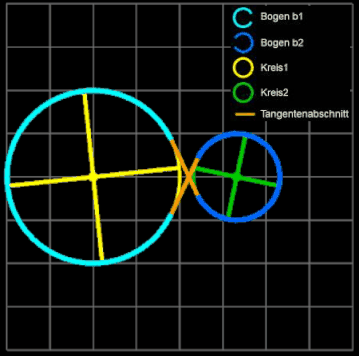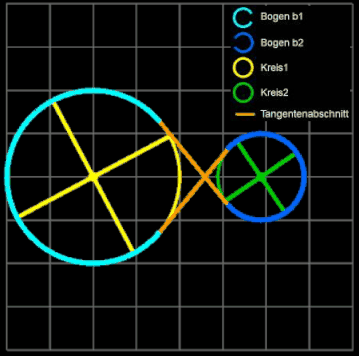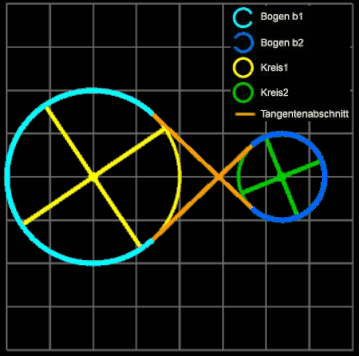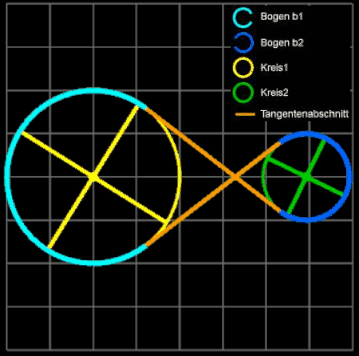
Für die Riemenlänge L ergibt sich
L = 2 • g + b1 + b2
b1 = π • r1 + 2 • r1 • α = r1 • (π + 2 • α)
b2 = r2 • (2 • π – 2 • (π /2 – α)
= r2 • (2 • π –π + 2 • α) = r2 • (π + 2 • α)
Für eine grundsätzliche Betrachtung und für einfache Animationen mögen die zuvor und die weiter oben berechneten Größen ausreichen.
Für die Konstruktion eines realen Riementriebs sind jedoch eine große Vielzahl von Parametern und Effekten zu beachten, siehe dazu z.B. [2], [3], [4].
Eine der wichtigen Größen bei einem Riementrieb ist der Umschlingungswinkel, d.h. der Kontaktbereich in Winkelgraden an, in denen der Riemen die Riemenscheibe umschließt. Generell gilt, dass ein größerer Umschlingungswinkel eine größere Kraftübertragung erlaubt (s. hierzu Euler-Eytelwein-Formel [5]).
Grundsätzlich ist der Umschlingungswinkel eines Riementriebs mit gekreuzten Riemen stets größer als bei einem Riementrieb mit nicht gekreuztem Riemen. Siehe hierzu die beiden nächsten Animationen mit den Umschlingungswinkeln α (Standardriementrieb) und β (gekreuzter Riemen); es gilt stets α < β.
Im Folgenden habe ich mich mit dem Graphing Calculator 3D etwas ausgetobt und weitere Varianten sowie Kombinationen mit Zahnrädern (s. auch 3D Zahnrad) erstellt:
Weiterführende technisch-physikalische Aspekte bezüglich des Riementriebs finden Sie z.B. in [2] und [3].