Nullstellenbestimmung - Verfahrensvergleich
Die folgende Tabelle zeigt wichtige Merkmale der drei "Standardverfahren" Sekanten-, Newton-, Halley-Verfahren zur numerischen Nullstellenbestimmung.
Für einige Funktionen wurden jeweils mit den drei Verfahren die Nullstellen sowie die Anzahl N (y-Achse) an erforderlichen Iterationsschritten für eine Genauigkeit von 10-15 bestimmt.
• f (x) =
x4 - x2 - 1
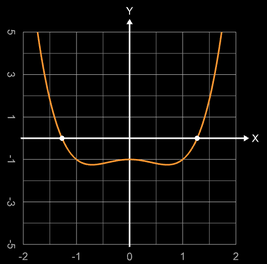
Das Polynom hat die Nullstellen {-1.272..., 1.272...}.
Bei x = -½ √2 und x = ½ √2 liegen lokale Minima (Tiefpunkte),
bei x = 0 liegt ein lokales Maximum (Hochpunkt).
Sekantenverfahren
x0 aus [-2.5, 2.5] (500 Punkte)
w = xi+1 - xi = 1.6
in allen Intervallen [xi, xi+1] liegt stets eine Nullstelle der Funktion, dennoch Divergenz in einigen Bereichen
Newton-Verfahren
Divergenz bei x = 0 (f hat dort ein relatives Maximum)
Halley-Verfahren
"Springen" zwischen den Nullstellen N1 und N2 im Bereich zwischen den Extremwerten; Divergenz bei x = 0 (f hat dort ein relatives Maximum)
• f (x) = 5 (x+1) x² (x-1)³
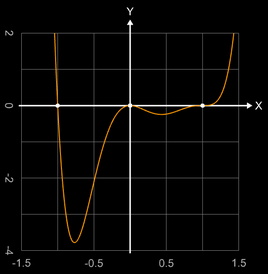
Das Polynom hat eine einfache Nullstelle bei x = -1,
eine doppelte Nullstelle bei x = 0
und eine dreifache Nullstelle (Terassenpunkt) bei x = 1.
Sekantenverfahren
Newton-Verfahren
Halley-Verfahren
• f (x) = sin (x)
Sekantenverfahren
in einem kleinen Bereich um die Nullstellen bei Vielfachen von π stabiles Verhalten
in einer Umgebung der Extremwerte bei Vielfachen von π / 2 Sprünge zu weit entfernten Nullstellen außerhalb [-10, 10] (weiße Linien) sowie Divergenz (schwarze Linie/Bereich)
Newton-Verfahren
Verhalten wie beim Sekantenverfahren
Halley-Verfahren
stabiles Verhalten im gesamten Intervall, keine Sprünge, DIvergenz bei x = 0
Konvergenzordnung und Effizienz
In der folgenden Grafik habe ich die auf meiner Webseite aufgeführten Verfahren zur Bestimmung der Nullstellen einer Funktion f hinsichtlich ihrer Konvergenzordnung q und ihrer Effizienz CE in einem Blasendiagramm positioniert.
Darüber hinaus zeigt eine entsprechende Einfärbung an, ob es sich um ein ableitungsfreies Verfahren (●) handelt oder ob die erste Ableitung (●) bzw. die erste und zweite Ableitung (●) der Funktion f verwendet werden.
Hinweis:
Um die CE-Werte in der obigen Grafik besser vergleichen zu können, wurden die Werte gerundet dargestellt, die sich ergeben gemäß:
1.260 ≈ 21/3 , 1.414 ≈ 21/2 , 1.431 ≈ 61/5 , 1.442 ≈ 31/3
, 1.495 ≈ 51/4 , 1.495 ≈ 51/4 ,1.554 ≈ (1+√2)1/2 , 1.565 ≈ 61/4 , 1.587 ≈ 41/3 , 1.618 ≈ Φ
.
Numerische Beispiele
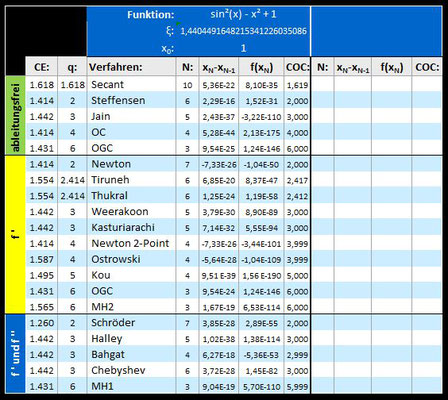
Die folgenden Tabellen zeigen für ausgewählte Funktionen f mit einer einfachen Nullstelle ξ für die oben aufgeführten Verfahren und zu einem gewählten Startwert x0 jeweils an:
N : Anzahl der benötigten Iterationsschritte
xN – xN-1 : Differenz zwischen N-tem Schritt und
Vorgänger
f (xN) : Funktionswert im N-ten
Schritt
COC (xN)
:
Computational Order of
Convergence im N-ten Schritt
CE: Effizienz
Als Abbruchkriterium der Iteration wurde für alle Verfahren | xi – xi-1 | ≤ 10-15 gewählt.
