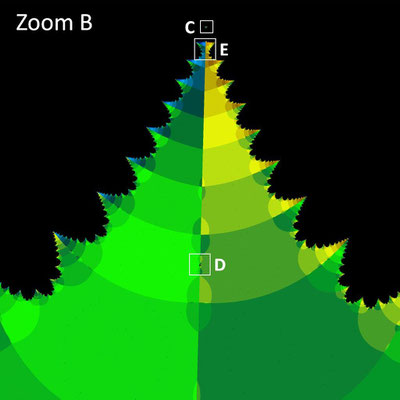
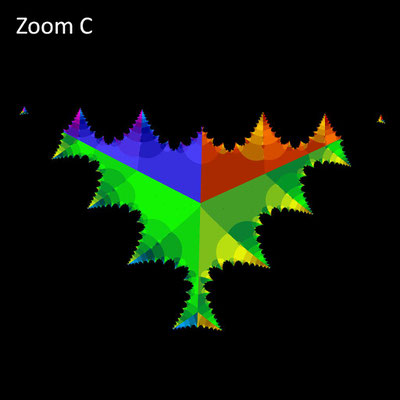
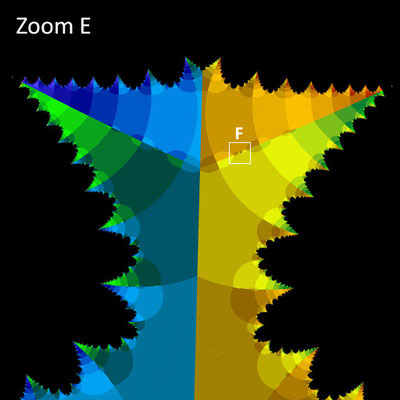
Basins of Attraction mit Laguerre-Verfahren für z^n - 1 = 0

z² - 1 = 0

Basins of Attraction z^2-1=0 Laguerre-Verfahren

z³ - 1 = 0

Basins of Attraction z^3-1=0 Laguerre-Verfahren

z⁴ - 1 = 0

Basins of Attraction z^4-1=0 Laguerre-Verfahren

B = [– (n – 1) ^{(2 / (n – 4))}, (n – 1) ^{(2 / (n – 4))} ] x [– (n – 1) ^{(2 / (n – 4))}, (n – 1) ^{(2 / (n – 4))} ]

Um Ladezeiten kurz zu halten, habe ich die Größe der Fraktale auf 1024 x 1024 Pixel beschränkt.

Klicken Sie auf ein Bild in der Galerie zur Anzeige von Polynomgrad n und B. Für eine weitere Vergrößerung klicken Sie auf die erscheinende Bildschirmlupe ). Innerhalb der Galerie bewegen Sie sich mit den Pfeiltasten ← → am linken / rechten Bildschirmrand.

Basins of Attraction z^5-1=0 Laguerre-Verfahren, B=[-16, 16]x[-16, 16]

Basins of Attraction z^5-1=0 Laguerre-Verfahren, B=[-0.4, 0.4]x[-0.4, 0.4]

Konvergenzverhalten z^5-1=0 Laguerre-Verfahren, B=[-16, 16]x[-16, 16]

Basins of Attraction z^6-1=0 Laguerre-Verfahren, B=[-5, 5]x[-5, 5]

Basins of Attraction z^6-1=0 Laguerre-Verfahren, B=[-0.5, 0.5]x[-0.5, 0.5]

Konvergenzverhalten z^6-1=0 Laguerre-Verfahren, B=[-5, 5]x[-5, 5]

Basins of Attraction z^8-1=0 Laguerre-Verfahren, B=[-2.5, 2.5]x[-2.5, 2.5]

Basins of Attraction z^8-1=0 Laguerre-Verfahren, B=[-0.6, 0.6]x[-0.6, 0.6]

Konvergenzverhalten z^8-1=0 Laguerre-Verfahren, B=[-2.5, 2.5]x[-2.5, 2.5]

Basins of Attraction z^9-1=0 Laguerre-Verfahren, B=[-2.3, 2.3]x[-2.3, 2.3]

Basins of Attraction z^9-1=0 Laguerre-Verfahren, B=[-0.7, 0.7]x[-0.7, 0.7]

Konvergenzverhalten z^9-1=0 Laguerre-Verfahren, B=[-2.3, 2.3]x[-2.3, 2.3]

Basins of Attraction z^12-1=0 Laguerre-Verfahren, B=[-1.8, 1.8]x[-1.8, 1.8]

Basins of Attraction z^12-1=0 Laguerre-Verfahren, B=[-0.75, 0.75]x[-0.75, 0.75]

Konvergenzverhalten z^12-1=0 Laguerre-Verfahren, B=[-1.8, 1.8]x[-1.8, 1.8]

Basins of Attraction z^16-1=0 Laguerre-Verfahren, B=[-1.6, 1.6]x[-1.6, 1.6]

Konvergenzverhalten z^16-1=0 Laguerre-Verfahren, B=[-1.6, 1.6]x[-1.6, 1.6]

Basins of Attraction und Konvergenzverhalten z^16-1=0 Laguerre-Verfahren, B=[-1.6, 1.6]x[-1.6, 1.6]

Basins of Attraction z^32-1=0 Laguerre-Verfahren, B=[-1.3, 1.3]x[-1.3, 1.3]

Basins of Attraction z^32-1=0 Laguerre-Verfahren, Zoomfaktor 23850

Konvergenzverhalten z^32-1=0 Laguerre-Verfahren, B=[-1.3, 1.3]x[-1.3, 1.3]

Basins of Attraction und Konvergenzverhalten z^32-1=0 Laguerre-Verfahren, B=[-1.3, 1.3]x[-1.3, 1.3]

Basins of Attraction z^128-1=0 Laguerre-Verfahren, B=[-1.2, 1.2]x[-1.2, 1.2]

Konvergenzverhalten z^128-1=0 Laguerre-Verfahren, B=[-1.2, 1.2]x[-1.2, 1.2]

Für eine größere, detailreichere Ansicht kicken Sie auf ein Bild in der Galerie, für eine weitere Vergrößerung auf die erscheinende Bildschirmlupe . Innerhalb der Galerie bewegen Sie sich mit den Pfeiltasten ← → am linken / rechten Bildschirmrand.

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom A

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom B

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom C

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom D

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom E

Basins of Attraction z^128-1=0 Laguerre-Verfahren, Zoom F

Quellenverweise

[1] P. Bělik, H. Kang, A. Walsh, E. Winegar (2014)
Analysis of Laguerre's method applied to find the roots of unity, arXiv:1405.0780