Trassierung
Der Begriff Trassierung beschreibt das Entwerfen und Festlegen der Linienführung ("Trasse") eines Verkehrsweges (Strassen, Bahnstrecken) in Lage, Höhe und Querschnitt.
Dazu werden mit Hilfe verschiedener Entwurfsmethoden Trassierungselemente zu einer räumlichen Linie zusammengefügt. Diese muss nicht nur fahrdynamischen und sicherheitsbezogenen Gesichtspunkten genügen, sondern sich auch gut in die Landschaft einfügen und möglichst geringe Massenbewegungen oder Bauwerke, wie z.B. Brücken oder Tunnel erfordern. Wesentlichen Einfluss auf die Trassierung nehmen auch sogenannte Zwangspunkte (z.B. Gebäude), die eine Anpassung der räumlichen Linie notwendig machen. Darüber hinaus gibt es noch weitere Aspekte, wie z.B. die Umwelt, Eigentumsverhältnisse, politische Gebietsgrenzen, finanzielle Mittel, fahrpsychologische Einflüsse, ästhetische Gesichtspunkte, etc. zu beachten.
Auch mit modernster Computertechnik ist die Trassierung eine komplexe Aufgabe für den Ingenieur und verlangt diesem umfachreiches Spezialwissen und Erfahrung ab.
Trassierung im Schulunterricht
Auch im Mathematikunterricht der Sekundarstufe II wird die "Trassierung" oftmals im Kontext Differential-rechnung behandelt, jedoch stark vereinfacht und eingeschränkt auf zweidimensionale Anwendungen (s. Kritische Anmerkungen am Ende dieser Seite).
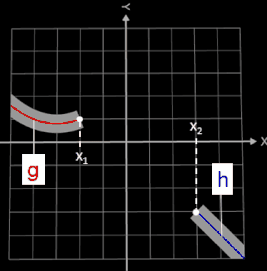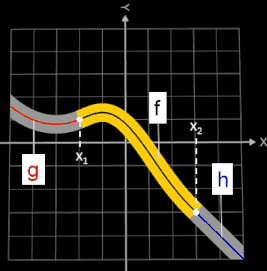
Gegenstand der Problemstellung dort sind in der Regel zwei vorgegebene Wegabschnitte, die durch einen dritten zu verbinden sind.
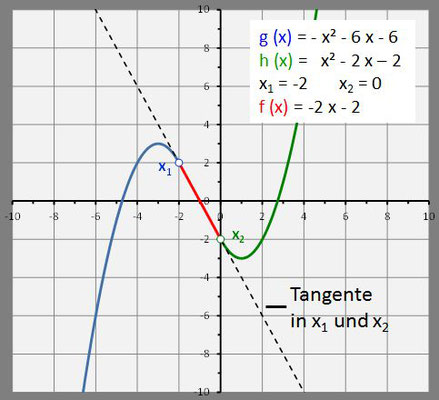
Modelliert wird das Ganze (s. Grafik), indem die vorgegebenen Wegabschnitte Teilgraphen zweier Funktionen g und h darstellen mit
g (x) , x ≤ x1
h (x) , x ≥ x2
x1 < x2
Das gesuchte Verbindungsstück zwischen x1 und x2 ist der Teilgraph eines Polynoms f.
Knickfreie Trassierung
Trivialerweise gilt, dass die Übergänge von g nach f an der Stelle x1 und von f nach h an der Stelle x2 versatzfrei sein müssen.
Ebenfalls direkt einsehbar im Sinne eines Straßen- oder Bahngleiseverlaufs ist die Forderung, dass diese Übergänge auch knickfrei sein müssen, d.h. g und f bzw. f und h besitzen an der Stelle x1 bzw. x2 jeweils die gleiche Steigung. Eine einfache Gerade als Verbindungsweg f scheidet somit in der Regel aus (s.u.). In eine mathematische Beschreibung umgesetzt ergibt sich demnach:
Forderung Bedingungen
- versatzfrei: g (x1) = f (x1) , f (x2) = h (x2)
-
knickfrei: g (x1) = f (x1)
, f
(x2) = h (x2)
g ' (x1) = f ' (x1) , f ' (x2) = h' (x2)
Soll nun ein knickfreier (und damit auch versatzfreier) Übergang mittels eines Polynoms f erzeugt werden, so kann dieses Polynom wegen der vier obigen Bedigungen maximal vom Grad drei sein, da dann vier unbekannte Koeffizienten a3, a2, a1 und a0 zu bestimmen sind.
Mit
f (x) = a3 x3 + a2 x2 + a1 x + a0
f ' (x) = 3 a3 x2 + 2 a2 x + a1
und x1, x2 ergibt sich für a3, a2, a1 und a0 somit folgendes Gleichungssystem:
das dann mit geeigneten Methoden zu lösen ist.
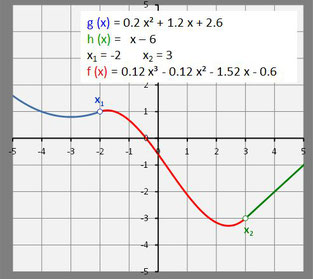
Hierzu ein Beispiel mit folgenden Wegabschnitten:
g (x) = 0.2 x² + 1.2 x + 2.6 x1 =
-2
h (x) = x - 6 x2 = 3
Mit
g ' (x) = 0.4 x + 1.2 g (-2) = 1 g ' (-2) = 0.4
h ' (x) = 1 h (3) = -3 h' (3) = 1
ergibt sich das Gleichungssystem in erweiterer Matrixschreibweise zu
mit der Lösung a3 = 0.12, a2 = -0.12, a1 = -1.52, a0 = -0.6. Die gesuchte knickfreie Verbindung ist also die Funktion f (x) = 0.12 x3 - 0.12 x2 - 1.52 x - 0.6.
Neben kubischen Funktionen können für eine knickfreie Verbindung bei den Polynomen f auch Geraden (dies nur, falls die Tangenten in x1 und x2 identisch sind, s. linkes Bild in folgender Galerie) oder Parabeln auftreten:
Krümmungsruckfreie Trassierung
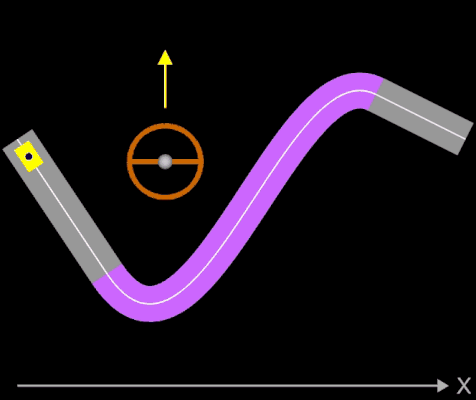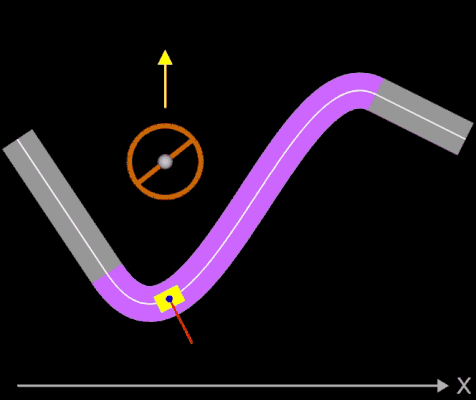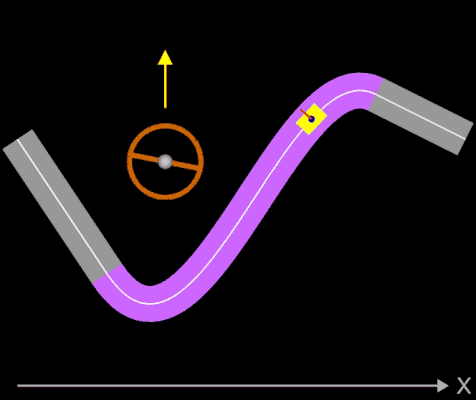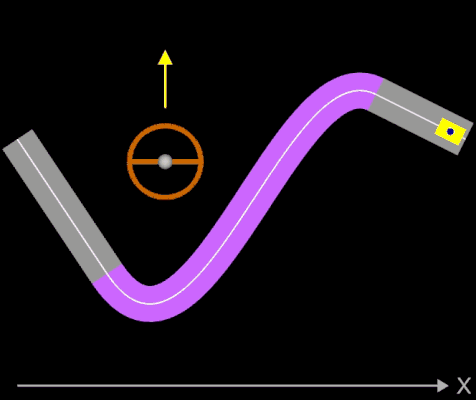
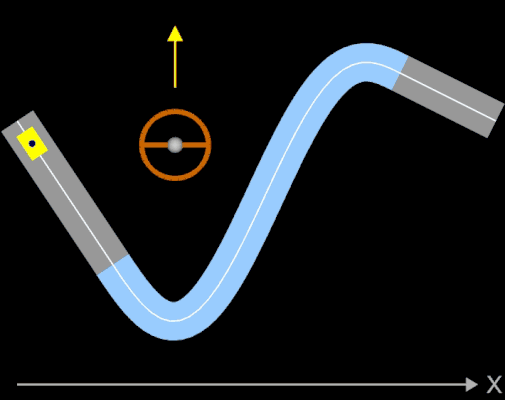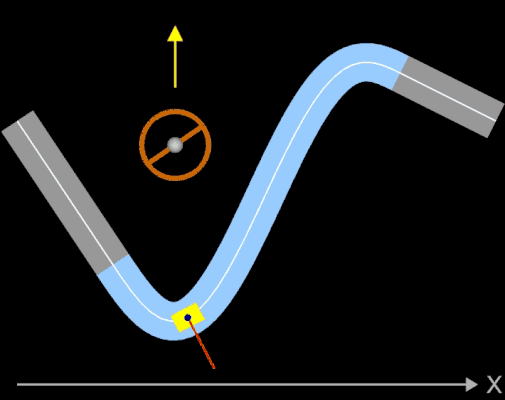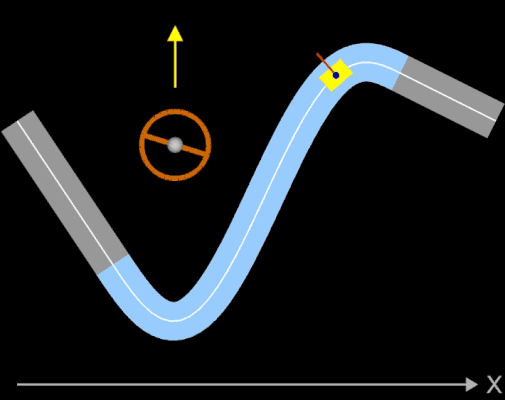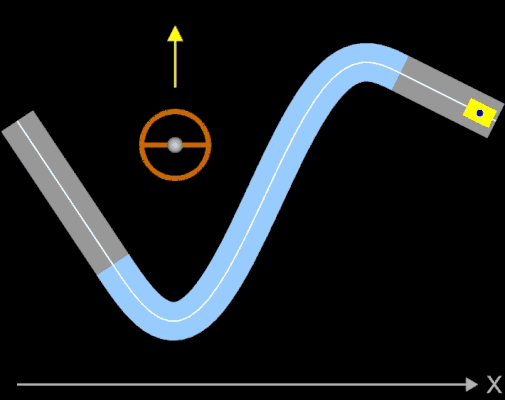
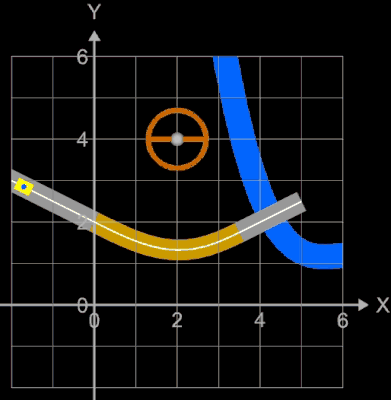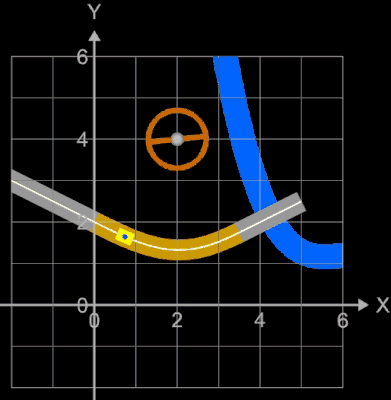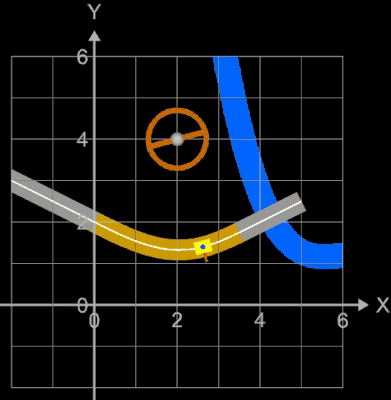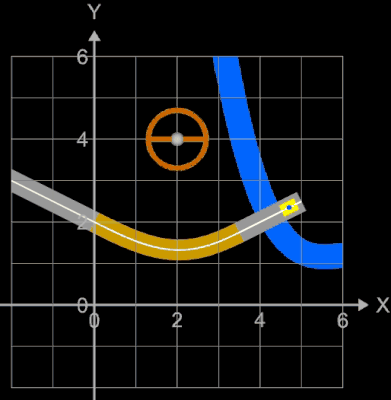
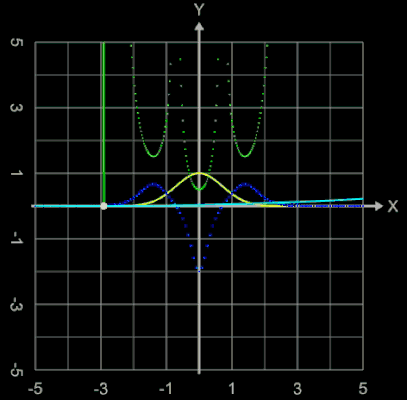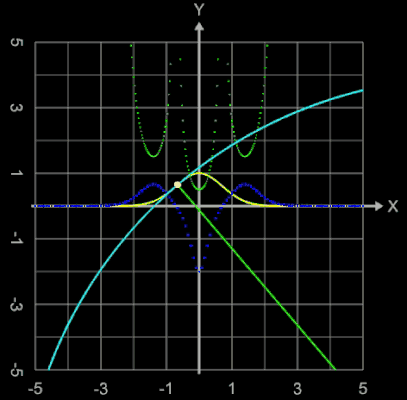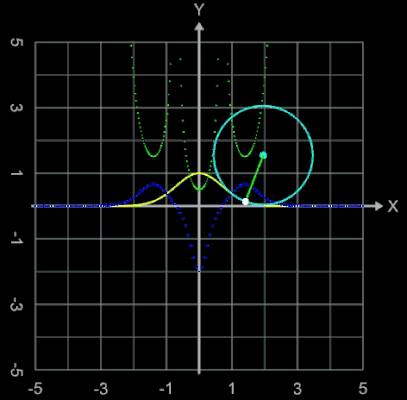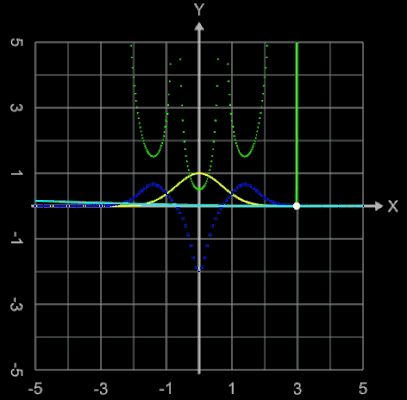
Die oben berechneten Bahnen (z.B. Straßenverläufe) mit knickfreien Teilstücken sehen auf den ersten Blick "vernünftig" aus. Sollen diese jedoch mit höheren Geschwindigkeiten befahren werden, sieht das Ganze anders aus. Dazu betrachte man folgende Animation, die jede(r) Autofahrer(in) direkt nachvollziehen kann:
Ein Fahrer fährt mit seinem Auto mit hoher Geschwindigkeit auf einem Kreisbogen (Viertelkreis). Da dessen Krümmung k konstant ist, kann der Fahrer bei optimaler Fahrweise das Steuerrad in einer fixen Position halten. Durch die Zentrifugalkraft (roter Vektor in der Animation) wird der Fahrer (blauer Punkt) nach außen gedrückt. Am Ende des Viertelkreises schließt sich plötzlich eine Gerade mit der Krümmung Null an. Der Fahrer muss nun schlagartig das Steuerrad in Geradeaus-Stellung bringen. Selbst wenn trotz der schlagartigen Lenkbewegung das Auto in der Spur bleibt, so wird der Fahrer ruckartig wieder in seine normale Sitzposition (oder darüber hinaus) bewegt - er (und das Auto) erfährt einen Ruck.
Dies ist natürlich bei der Trassierung nicht erwünscht! Vielmehr müssen die Übergänge an den Stellen x1 und x2 nicht nur knickfrei, sondern auch krümmungsruckfrei sein. Daher muss gelten, dass die Krümmung der Funktionen g und f an der Stelle x1 und ebenso die Krümmung der Funktionen f und h an der Stelle x2 jeweils gleich sind. Für das Polynom f als Verbindungsstück muss daher gelten:
-
krümmungsruckfrei: g
(x1) = f (x1) , f (x2) = h (x2)
g ' (x1) = f ' (x1) , f ' (x2) = h' (x2)
g '' (x1) = f '' (x1) , f '' (x2) = h'' (x2)
Für einen krümmungsruckfreien (und damit auch versatz- und knickfreien) Übergang mittels eines Polynoms f kann dieses wegen obiger sechs Bedigungen maximal vom Grad fünf sein, da dann sechs unbekannte Koeffizienten a5, a4, a3, a2, a1 und a0 zu bestimmen sind.
Mit
f (x) = a5 x5 + a4 x4 + a3 x3 + a2 x2 + a1 x + a0
f ' (x) = 5 a5 x4 + 4 a4 x3 + 3 a3 x2 + 2 a2 x + a1
f '' (x) = 20 a5 x3 + 12 a4 x2 + 6 a3 x + 2 a2
und x1, x2 ergibt sich für a5, a4, a3, a2, a1 und a0 folgendes Gleichungssystem:
Angewandt auf das obige Beispiel mit kubischem, knickfreiem Verbindungsstück ergibt sich mit g '' (x) = 0.4 und h '' (x) = 0 das Gleichungssystem
und somit die Funktion
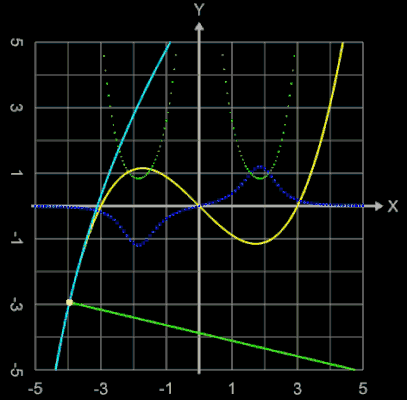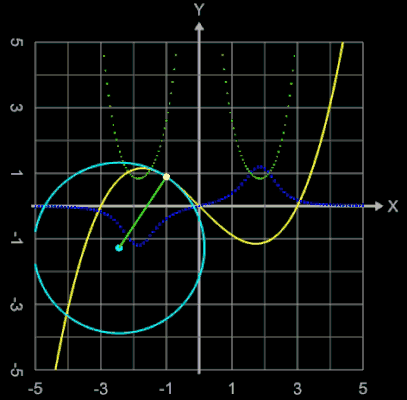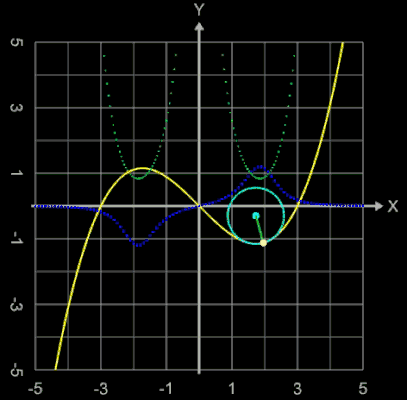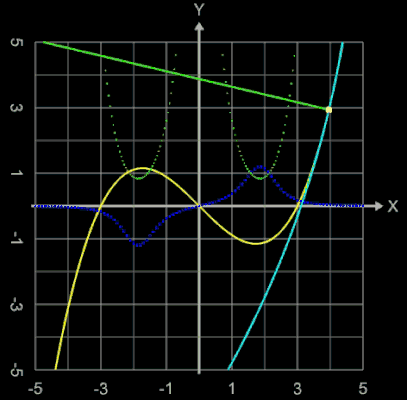
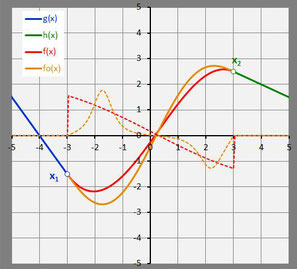
Die folgende Grafik zeigt die knickfreie Variante mit der kubischen Funktion f und die krümmungsruckfreie Variante mit dem Polynom fünften Grades fo zum Vergleich. Zusätzlich wurde dort auch der Krümmungsverlauf k (x) des Gesamtweges (gestrichelte Linie) eingezeichnet.
Zum eigenen "Experimentieren" steht unten im Download-Bereich eine EXCEL-Datei bereit, mit der auch die obigen Trassierungen und Grafiken erstellt wurden.
Die folgenden beiden Animationen sollen noch einmal das Problem der Krümmungsruckfreiheit anhand eines Straßenverlaufs mit fahrendem Auto veranschaulichen.
Die vorgegebenen Straßenabschnitte sind g (x) = -1.5 x - 6,
h (x) = -0.5 x + 4, x1 = -3, x2 =3 (s.Abbildung rechts).
Für die knickfreie Trassierung ergibt sich
f (x) = - 5/54 x³ + 1/12 x² + 3/2 x - 1/4,
für die krümmungsruckfreie
fo (x) = 5/648 x5 -1/432 x4 - 25/108 x3 + 1/8 x2 + 17/8 x - 7/16.
Das eingezeichnete Lenkrad (weißer Pfeil zeigt in Fahrtrichtung) zeigt die erforderlichen Lenk-bewegungen, der rote Strich am "Fahrer" (blauer Punkt) zeigt die auf ihn wirkende Zentrifugalkraft.
Die "Straße" sowie das Fahrzeug wurden mittels eines Rohrs, das die Funktionen ummantelt und bei dem die z-Komponente zu Null gesetzt wurde, erzeugt (s. bei Funktionsgraph als Rohr/Röhre).
________________
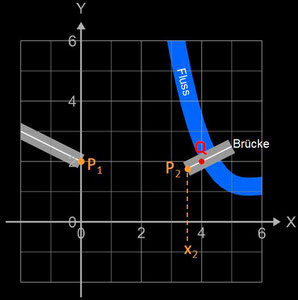
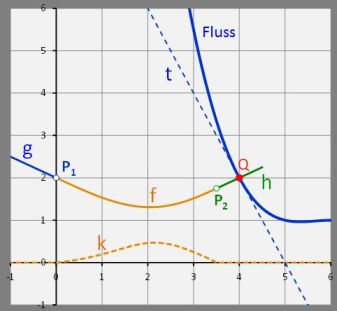
Abschließend soll noch eine Trassierung für eine leicht veränderte Aufgabenstellung durchgeführt werden. Hierbei sind folgende Fakten gegeben (s. Grafik rechts):
- g (x) = - 0.5 x + 2
- x1 = 0
- x2 = 3.5
- Die geradlinige Brücke verläuft senkrecht zum Fluss, dessen linkes Ufer durch die Funktion
L (x) = -0.25 x³ + 4.25 x² - 24 x + 46 dargestellt werden kann. - Im Punkt Q (4|2) befindet sich die Brücke genau über dem linken Flussufer.
Das krümmungsruckfreie Anschlussstück soll zwischen P1 und P2 angelegt werden.
Lösung:
Es ist g ' (x) = - 0.5, g '' (x) = 0.
Der Brückenabschnitt ist geradlinig, die den Brückenabschnitt bildende lineare Funktion h ist jedoch unbekannt. Da aber h im Punkt Q (4|2) senkrecht zur Funktion L (linkes Flussufer) verläuft, mithin eine Normale zur Tangente t an L in Q bildet (s. folgende linke Grafik), gilt dort für h
Mit L' (x) = -0.75 x² + 8.5 x - 24 und L' (4) = -2 ergibt sich h ' (x) = 0.5. Durch Einsetzen der Koordinaten von Q in die Punkt-Steigungs-Form einer Geraden ergibt sich h (x) = 0.5 x, h (3.5) = 1.75 sowie h '' (x) = 0.
Somit ergibt sich für das krümmungsruckfreie Anschlussstück das folgende Gleichungssystem nebst Lösung:
Die Lösung zusammen mit der Tangente t und dem Krümmungsverlauf k zeigt die folgende linke Grafik, eine Animation für das Befahren der Wegstrecke ist in der rechten Grafik zu sehen.
Intermezzo: Zweite Ableitung und Krümmung
Bezüglich des Begriffs "Krümmung" sei an dieser Stelle ein kleines Intermezzo eingeschoben. So passierte es hin und wieder in meinem Unterricht zur Themenreihe Differentialrechnung, dass nach der Einführung der Ableitungen einer Funktion und deren Bedeutungen angesichts der Funktion f (x) = x² eine "ausgeschlafene" Schülerin fragte, wie es denn sein könne, "dass mit der zweiten Ableitung für die Krümmung überall 2 rauskommt, obwohl die Parabel für große x-Werte fast gerade und im Bereich des Scheitelpunkts stark gekrümmt ist"…
Oups – ein Fall "kognitiver Dissonanz" und - insbesondere wegen des bis dato fehlenden Unterrichtsstoffs (arctan-Funktion) und mathematischer Werkzeuge (Kettenregel) für die Herleitung des Begriffs "Krümmung eines Funktionsgraphen" - eine echte Herausforderung für den Mathelehrer! Zumindest kann man in solch einem Moment folgendes klarstellen:
-
Eine Funktion ist bekanntlich eine Zuordnung, wobei jedem Element x einer
Definitionsmenge D genau ein Element y einer Wertemenge W
zugeordnet wird:
- Der Funktionsgraph ist eine grafische Interpretation / Modell des (abstrakten) mathematischen Objekts Funktion, indem die Wertepaare (x | y) in die x/y-Ebene (kartesisches Produkt aus Definitionsmenge D und Wertemenge W) eingetragen werden. Es ergibt sich eine geometrische Figur (Kurve), wie z.B. eine Gerade für die lineare Funktion y = f(x) = a • x + b oder eine Parabel für die quadratische Funktion y = f (x) = a • x² + b • x + c (a ≠ 0).
- Die erste Ableitung in einem Punkt (x0 | y0) gibt die Steigung der Funktion im Punkt (x0 | y0) an. Dies entspricht beim Funktionsgraph der Steigung der Tangente im Punkt (x0 | y0).
- Die zweite Ableitung f '' in einem Punkt (x0 | y0) gibt die Krümmung der Funktion f im Punkt (x0 | y0) an. Ist ihr Wert dort positiv, so ist die Funktion "linksgekrümmt", ist er negativ, so ist die Funktion dort "rechtsgekrümmt". Tatsächlich (und wie zu erwarten war) zeigt das geometrische Objekt Funktionsgraph (Kurve) das gleiche Krümmungsverhalten wie die Funktion, wie z.B. eine Linkskrümmung bei der Normalparabel. Die Krümmung eines Funktionsgraphen im Punkt (x0 | y0) ist ein Maß für die Richtungsänderung der Tangente in diesem Punkt.
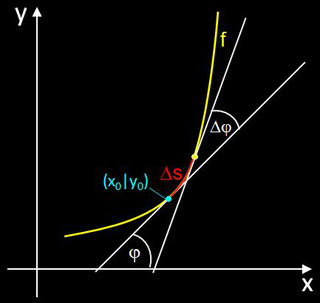
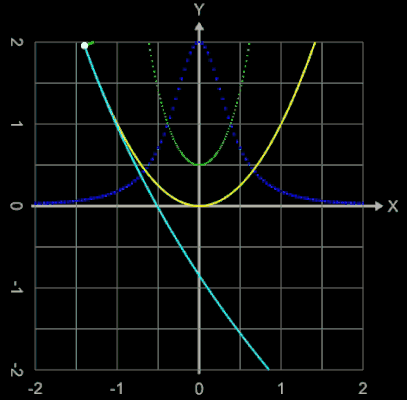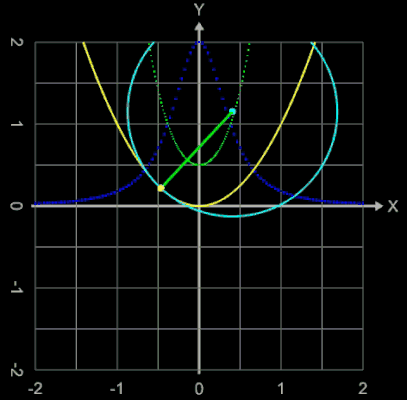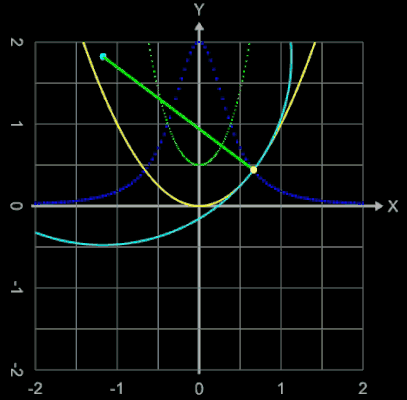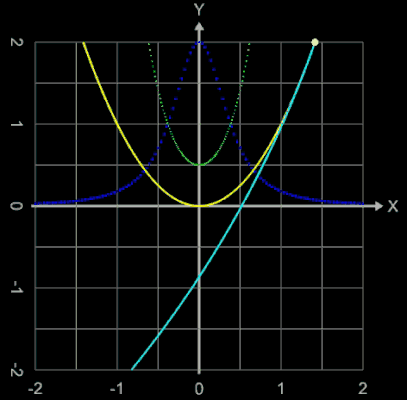
Um für eine Kurve die geometrische Krümmung in einem Punkt (x0 | y0) zu ermitteln, betrachte man die nebenstehende Grafik.
Die Tangente im Punkt (x0 | y0) bildet mit der x-Achse einen Winkel φ. Wandert man auf der Kurve ausgehend vom Punkt (x0 | y0) eine kleine Wegstrecke ∆s weiter, so entsteht zwischen den Tangenten an beiden Punkten eine Winkeldifferenz ∆φ.
Die Krümmung κ ist definiert als das Maß, wie stark sich dieser Winkel ändert:
Ist die Kurve ein Funktionsgraph einer Funktion f, so ergibt sich für die Krümmung zu
(Anmerkung: Ich verzichte hier auf eine Herleitung; der interessierte Leser findet eine solche z.B. bei [1]).
Es lassen sich somit folgende Aussagen treffen:
- Die Krümmung ist vorzeichenbehaftet durch das Vorzeichen von f '' (x); ist f '' (x0) > 0, so ist die Kurve an x0 linksgekrümmt, ist f '' (x0) < 0, so ist die Kurve an x0 rechtsgekrümmt.
- Ist f '' (x0) = 0, wie z.B. in einem Wendepunkt, so ist κ (x0) = 0.
- Ist f ' (x0) = 0, liegt also an der betrachteten Stelle eine waagrechte Tangente vor, wie z.B. an einem Extremwert, so gilt κ (x0) = f '' (x0).
Übrigens ...
Eine konstante Krümmung κ besitzen nur die Gerade (κ = 0) sowie der Kreis (Radius r : κ = 1 / r).
Die folgende Grafik zeigt für das Beispiel der Funktion f (x) = x² den Funktionsgraph (Normalparabel), ihre zweite Ableitung f '' (x) = 2 sowie den Graph der Krümmungsfunktion κ (x), die jedem x-Wert die Krümmung des Funktionsgraphen von f zuordnet und natürlich genau die Beobachtung der oben zitierten Schülerin wiedergibt.
________________
Krümmungskreis
Eng verknüpft mit dem Begriff Krümmung einer ebenen Kurve im Punkt (x0 | y0) ist der Krümmungskreis (auch Schmiegekreis genannt) zum Punkt (x0 | y0), der die Kurve in diesem Punkt am besten annähert. Den Mittelpunkt des Krümmungskreises nennt man Krümmungsmittelpunkt. Sein Radius, der Krümmungsradius, ist der Betrag des Kehrwerts der Krümmung κ der Kurve im Punkt (x0 | y0). Seine Tangente in diesem Punkt stimmt mit der Tangente der Kurve überein.
Da die Krümmung einer Kurve im Allgemeinen örtlich variiert, schmiegt sich der Krümmungskreis meist nur in einer infinitesimal kleinen Umgebung der vorgegebenen Kurve an. Er verläuft auf der einen Seite des Berührungspunktes innerhalb und auf der anderen Seite außerhalb der Kurve, er schneidet also die Kurve in einem gewissen Abstand vom Punkt (x0 | y0). Nur wenn die Krümmung der Kurve bei (x0 | y0) ein Extremum hat, schmiegt sich der Kreis auf einer längeren Strecke der Kurve an diese an, wie man es auch in den folgenden Animationen, die Krümmungskreise beim Überfahren der Funktionsgraphen verschiedener Funktionen zeigen, beobachten kann. Pro Grafik ist dort folgendes dargestellt:
Übrigens ...
In einem Wendepunkt des Funktionsgraphens von f (dort ist f '' (x) = 0) ist der Krümmungsradius r = ∞.
Trassierung im Schulunterricht <> Trassierung in der realen Welt
Anhand der typischen Trassierungsaufgaben im Schulunterricht (s.o.) könnten die Schüler(innen) den Eindruck gewinnen, dass sie mit einem Polynoms 3., 4. oder 5. Grades eine ideale Trassierung berechnet hätten und dass die gesamte Thematik "gar nicht so schwer" sei. Dem ist aber nicht so! Hier sind einige Kritikpunkte angebracht ...
- Ein erster Kritikpunkt ist die Reduktion einer Straße mit einer gewissen Breite auf eine unendliche dünne Linie (Funktionsgraph). So kann jede(r) Autofahrer(in) bei hinreichender Straßenbreite einen etwas anderen Weg fahren, als ihm die Straßenachse vorschreibt. Im Allgemeinen wird er/sie die Kurven etwas anschneiden, um das plötzliche Einschlagen der Lenkräder am Bogenanfang zeitlich zu verlängern und somit die auftretenden Fliehkraftwechsel (Seitenruck) zu vermindern.
Weiterhin wünscht sich jede(r) Autofahrer(in) einen Straßenverlauf mit konstanten Krümmungen – also Geraden und Kreisbögen – um Lenkbewegungen zu minimieren. Tatsächlich bestanden die in den 1930er und 1940er gebauten Autobahnen in Deutschland ausschließlich aus Geraden und Kreisbögen.
Die Eisenbahnen, welche gegen Ende des 19. Jahrhunderts schon große Fahrgeschwindigkeiten erreichten, begannen schon damals ihre Kurven zu überhöhen und zwischen Gerade und Kreisbogen eine Übergangskurve in Form eines Polynoms 3. Grades ("kubische Parabel") einzubauen. In den 30er Jahren des letzten Jahrhunderts, als mit der Verbesserung der Motorfahrzeuge die Geschwindigkeiten auf den Landstraßen immer größer wurden, hielten diese Übergangskurven allmählich auch Einzug in den Straßenverkehr. Der Fahrer wurde durch die "kubische Parabel" in die eigentliche Kreiskurve übergeführt, hatte dadurch ausreichend Zeit, das Steuerrad entsprechend dem Kurvenradius einzuschlagen, und der Aufstieg vom dachförmigen Straßenprofil zur einseitigen Kurvenüberhöhung ließ sich so mühelos bewerkstelligen.
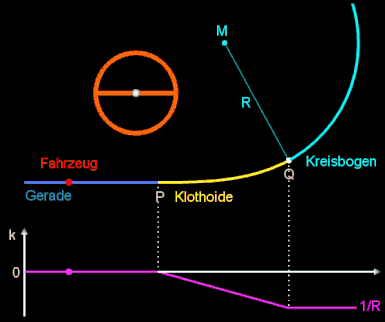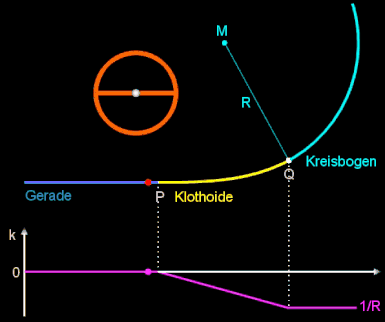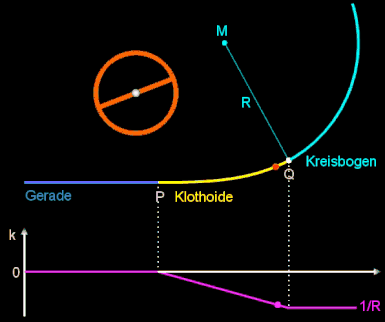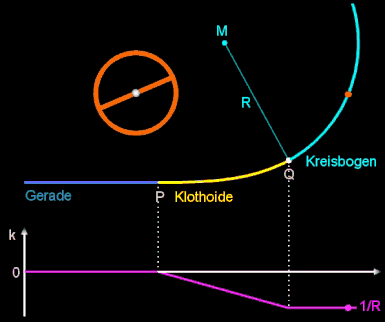
Durch theoretische Studien / Untersuchungen sowie Fahrversuche bezüglich der Kurvenausbildung konnte jedoch bald nachgewiesen werden, daß die "kubische Parabel" den fahrtechnischen Eigenschaften der schnellen Straßenfahrzeuge nicht voll gerecht wird. Bei einer idealen Übergangskurve zwischen Gerade und Kreisbogen muß sich die Krümmung proportional zur Weglänge ändern.
Dies führt zu einem Übergangsbogen in Form einer Klothoide. Bei dieser Kurve ist die Krümmung k proportional zur
Länge L (identisch mit "Krümmungsradius R ist umgekehrt proportional zur Länge L")
(s. Klothoide):
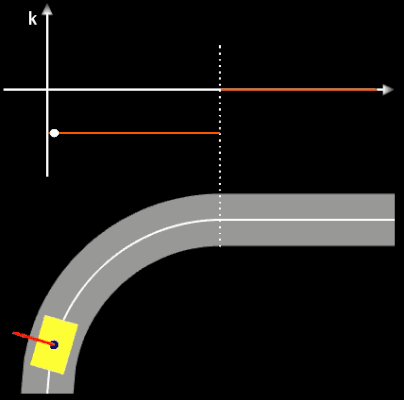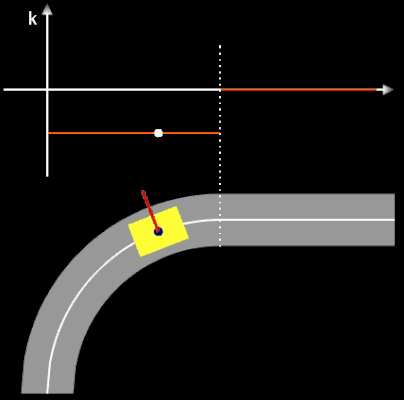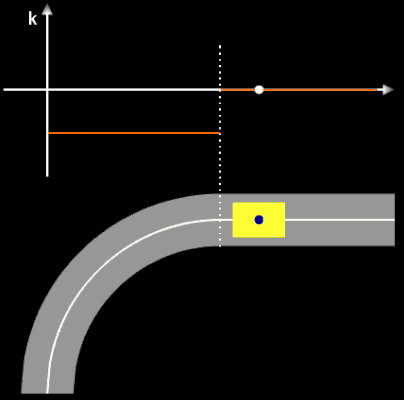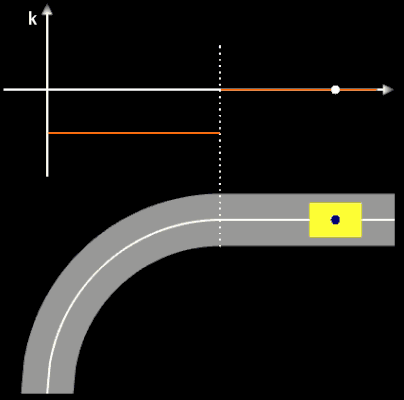
wobei die positive Konstante A der Klothoidenparamter ist und R der Radius des Krümmungskreises (s.o.) am Endpunkt der Klothoide. Die folgende Animation zeigt die Verbindung einer Geraden (k = 0) und einem Kreisbogen mit Radius R mittels einer Klothoide als Übergangsbogen sowie darunter den Verlauf der Krümmung k beim Durchfahren dieser Wegstrecke.
Zwar war die Klothoide schon lange bekannt. Da die exakte Berechnung aber nicht in geschlossener Form möglich ist, sondern numerisch erfolgen muss (vgl. Klothoide) und wegen der damals fehlenden Rechnerkapazitäten hielt die Klothoide erst Ende der 1930er Jahre allmählich Einzug in den
Straßenbau. Jedoch ist bereits 1995 in den Richtlinien für die Anlage von Landstraßen und Autobahnen, Abschnitt 4.3
(S. 14) ein Übergangsbogen in Form einer Klothoide bereits zwingend vorgegeben [2] :
"Der Übergangsbogen soll
- durch seine allmähliche Krümmungsänderung einen stetigen Linienverlauf gewährleisten und damit eine gleichmäßige Geschwindigkeit sowie eine kontinuierliche Änderung der bei der Kurvenfahrt auftretenden Zentrifugalbeschleunigung ermöglichen,
- als Übergangsstrecke für die Fahrbahnverwindung dienen und
- eine optisch befriedigende Lininenführung bewirken.
Seine Anwendung ist bei allen Straßen erforderlich. Der Übergangsbogen wird als Klothoide ausgebildet."
Damit die zuvor genannten Ziele erreicht werden, schreiben die aktuellen Regelwerke für die Anlage von Landstraßen und Autobahnen [3], [4] für den Klothoidenparameter A folgende Bedingung vor:
Damit ist sicher gestellt, dass sich die Klothoide nicht so stark "eindreht" (A ≤ R, τ ≤ 31,8 gon = 28.62°), andererseits aber der Übergangsbogen optisch erkennbar ist (A ≥ R/3, τ ≥ 3,5 gon = 3.15°).
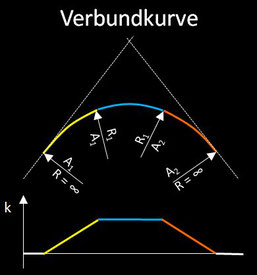
Weiterhin werden umfangreiche Einsatz- und Zusatzbedingungen (vor allem im Hinblick auf die zulässige Höchstgeschwindigkeit) sowie diverse Ausnahmefälle (z.B. bei topographischen Problemfällen) spezifiziert. Insbesondere werden unter den möglichen Linienführungen die zwei folgenden empfohlen:
Einsatzbedingungen:
Die Radienfolge ist nach Abschnitt 5.5.5 abzustimmen.
Beide Äste der Wendeklothoide sollten gleiche Parameter (A2 ≈ A3) aufweisen. Bei unsymmetrischer Ausbildung soll das Verhältnis A1 : A2 ≤ 1.5 betragen.
Zwischengeraden zwischen den beiden Ästen der Wendeklothoide dürfen die Länge
LZ ≤ 0.08 (A2 + A3) nicht überschreiten.
Eine sehr gute und auch für den Laien (wie mich) verständliche Darstellung mit praktischen Beipielen
für die Trassierung auf Grundlage der RAL [3] und RAA [4] mit Geraden,
Kreisbögen und Klothoiden
findet man bei [5].
Für die Berechnung von Klothoiden siehe auch den Abschnitt Näherungsformeln für die Anwendung im Straßenbau unter Klothoide.
________________
Und hier setzt mein zweiter (und wichtigerer) Kritikpunkt an:
2. Die Schüler(innen) leiten ein Polynom 3. bis 5. Grades als
Verbindungsstück her und sind der Meinung, dass sie somit das Trassierungsproblem gelöst hätten. Haben sie aber nicht!
Denn in der Realität sind die zulässigen Trassierungselemente Geraden, Kreisbögen und Klothoiden.
Hier müsste im Unterricht auf die historische Entwicklung mit Blick auf die Linienführung eingegangen werden, d.h. von der Kombination Gerade-Kreisbogen, über Gerade -"kubische Parabel"-Kreisbogen bis hin zu Gerade-Klothoide-Kreisbogen. Es ist aber anzunehmen, dass die Zeit dafür nicht da ist ...
Dennoch sind Trassierungsaufgaben wie die oben dargestellten Bestandteil von Prüfungsaufgaben im Abitur, teils mit "abenteuerlichen" Randbedingungen und anderen Funktionstypen (z.B. Exponential-, Logarithmus-, trigonometrische Funktionen) für den Straßenverlauf. Im Internet findet man dazu zahlreiche Lösungswege und Erklärvideos, ebenso aber auch kritische Betrachtungen aus der Fachrichtung Mathematikdidaktik kommend, wie z.B. bei [6].
Falls Sie als Leser bezüglich meiner Kritik anderer Meinung sind, würde ich mich über einen Kontakt freuen. Dass das Thema Trassierung hier Einzug auf meine Webseite gehalten hat, ist übrigens einer angehenden Mathematiklehrerin zu verdanken, die auf der Suche nach einer Visualisierung auf meine 3D Kugelbahn (eigentlich eine kleine Spielerei) stieß und fragte, ob man eine derartige Visualisierung nicht auch für "Straßen" machen könne. Ja ... kann man ... siehe weiter oben ...
Quellenverweise
[1] wikipedia.org/wiki/Krümmung
[2] Bundesministerium für Verkehr, Richtlinien für die Anlage von Straßen RAL (1995),
https://de.scribd.com/doc/68065554/RAS-L-1995-Horizontal-Alignment
[3] Bundesministerium für Verkehr, Bau- und Stadtentwicklung, Richtlinien für die Anlage von
Landstraßen
RAL (2012), Kap. 5 Linienführung, S.37
[4] Bundesministerium für Verkehr, Bau- und Stadtentwicklung, Richtlinien für die Anlage von
Autobahnen
RAA (2008), Kap. 5 Linienführung, S.27-28
[5] K. Habermehl, R. Weber, Entwurfselemente im Lageplan,
Lehrveranstaltung Verkehrswesen 2 (Modul
3305),Hochschule Darmstadt
[6] A. Lambert, U. Peters, Straßen sind keine Splines, Universität des Saarlandes (2005),
http://dx.doi.org/10.22028/D291-26287
Download
Die folgende EXCEL-Datei berechnet Polynome als Trassierungselemente und stellt diese grafisch dar. Ich habe sie bewusst einfach aufgebaut. So wurde z.B. auf Überprüfungen der manuellen Eingabe sowie auf VBA-Elemente verzichtet. Somit können interessierte Leser(innen) das Tabellenblatt ganz einfach auf ihre Bedürfnisse anpassen.