Zwei-Schritt-Verfahren (two-step methods)
Bei den Zwei-Schritt-Verfahren (two-step methods) wird für jeden Iterationsschritt i zunächst ein Zwischenwert (predictor) berechnet. Üblicherweise wird hierzu das Newton-Verfahren verwendet. Der Zwischenwert wird dann mit dem "eigentlichen" Verfahren verbessert (corrector) (vgl. Erklärung beim Ostrowski-Verfahren für reelle Funktionen).
Die Anwendung der im folgenden betrachteten Verfahren auf eine Vielzahl komplexer Funktionen finden Sie unter Basins of Attraction.
- Jain-Verfahren (komplex)
- Ostrowski-Verfahren (komplex)
- Kou-Li-Wang-Verfahren (komplex)
- Chun I -Verfahren (komplex)
- King-Verfahren (komplex)
- Chun II -Verfahren (komplex)
- Chun III -Verfahren (komplex)
- Feng-Verfahren (komplex)
- Contra Harmonic Newton-Verfahren (komplex)
- Kung-Traub-Verfahren (komplex)
- Fang-Ni-Cheng-Verfahren (komplex)
- Rafiq-Rafiullah-Verfahren (komplex)
- Chun-Kim II -Verfahren (komplex)
- Chun-Kim III -Verfahren (komplex)
- Weerakoon-Fernando-Verfahren (komplex)
- Sharma-Bahl-Verfahren (komplex)
- Chun-Lee-Neta-Verfahren (komplex)
- Jarratt-Verfahren (komplex)
- Solaiman-Hashim-Verfahren (komplex)
- Ham-Chun-Verfahren (komplex)
- Fang-Sun-He-Verfahren (komplex)
- Ghanbari-Verfahren (komplex)
- Chun-Ham I -Verfahren (komplex)
- Ardelean-Verfahren (komplex)
- Kou-Li-Liu-He-Verfahren (komplex)
- Chun-Ham II -Verfahren (komplex)
- Kou-Li-Verfahren (komplex)
- Chun-Neta-Verfahren (komplex)
• Jain-Verfahren für komplexe Funktionen
Angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ lautet die Iterationsvorschrift für das Jain-Verfahren
Für die Herleitung, weitere Details, Konvergenzordnung q, Effizienzindex CE siehe unter Jain-Verfahren für reelle Funktionen.
• Ostrowski-Verfahren für komplexe Funktionen
Das Ostrowski-Verfahren ist ein 2-Schritt-Verfahren; für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ beruht es auf der Iterationsvorschrift
Für weitere Details, Konvergenzordnung q und Effizienzindex CE siehe Ostrowski-Verfahren für reelle Funktionen.
• Kou-Li-Wang-Verfahren für komplexe Funktionen
Kou, Li und Wang stellten zur Nullstellenbestimmung komplexer Funktionen f : D → ℂ mit D ⊆ ℂ folgende Iterationsvorschrift auf:
Es handelt sich um ein 2-Schritt-Verfahren mit der Konvergenzordnung q = 4 und dem Effizienz-Index
CE = 1.587.
Das Verfahren ist für β = 1 identisch mit dem King-Verfahren.
Quellenverweise
[1] J. Kou, Y. Li, X. Wang (2007), A composite fourth-order iterative method for solving non-linear
equations, Applied Mathematics and Computation, Vol. 184, Issue 2, Jan. 2007, (471-475)
https://doi.org/10.1016/j.amc.2006.05.181
• Chun-Verfahren (I) für komplexe Funktionen
In [1] (Gleichung 10) publizierte C. Chun ein Verfahren zur Nullstellenbestimmung, das für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ auf folgender Iterationsvorschrift basiert:
Es besitzt die Konvergenzordnung q = 4 bei einem Effizienzindex CE = 1.414 und ist für β = 2 identisch mit dem King-Verfahren.
Quellenverweise
[1] C. Chun (2005), Iterative Methods Improving Newton's Method by the Decomposition Method,
Computers and Mathematics with Applications 50 (2005) 1559-1568,
doi:10A016/j.camwa.2005.08.022
• King-Verfahren für komplexe Funktionen
R. F. King [1], [2] erzeugt für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ mit der Iterationsvorschrift
und dem Parameter β eine Familie von 2-Schritt-Verfahren mit der Konvergenzordnung q = 4 und dem Effizienz-Index CE = 1.587 (s. dazu auch Iterative Verfahren zur Bestimmung von Nullstellen).
Für einige Werte β von ergeben sich folgende andere Verfahren:
- β = 0: es ergibt sich das Ostrowski-Verfahren
-
β = 1: identisch mit dem Verfahren Verfahren von Kou-Li-Wang
- β = 2: entspricht dem Verfahren von Chun I
Quellenverweise
[1] R.F. King, A family of fourth order methods for nonlinear equations (1973),
SIAM J. Numer. Anal. 10 (1973), (876–879), https://www.jstor.org/stable/2156321
[2] J. R. Sharma et al. (2012),
Improved
King’s methods with optimal order of convergence based on
rational approximations, Applied Mathematics
Letters, Volume 26, Issue 4, April 2013, (473-480),
https://www.sciencedirect.com/science/article/pii/S0893965912004739
• Chun-Verfahren (II) für komplexe Funktionen
Das von C. Chung entwickelte zweistufige Verfahren [1] ist eine Weiterentwicklung des Newton-Verfahren mit der Konvergenzordnung q = 3 und dem Effizienzindex CE = 1.316. (s. dazu auch Iterative Verfahren zur Bestimmung von Nullstellen). Angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ lautet die Iterationsvorschrift:
Quellenverweise
[1] C. Chun (2006), Construction of Newton-like iteration methods for solving nonlinear equations,
Numer. Math. (2006) 104:
297–315, DOI
10.1007/s00211-006-0025-2
• Chun-Verfahren (III) für komplexe Funktionen
Eine Weiterentwicklung des Newton-Verfahren von C. Chung ist das zweistufige Verfahren (s. [1], Gleichung (57) mit h = -1) mit folgender Iterationsvorschrift für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ:
Es besitzt die Konvergenzordnung q = 3 und den Effizienzindex CE = 1.442 (s. dazu auch Iterative Verfahren zur Bestimmung von Nullstellen).
Quellenverweise
• Feng-Verfahren für komplexe Funktionen
Das von J. Feng aufgestellte 2-stufige Verfahren basiert für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ auf der Iterationsvorschrift [1]:
Es besitzt lediglich quadratische Konvergenz (q = 2) und hat den Effizienzfaktor CE = 1.189 (s. dazu auch Iterative Verfahren zur Bestimmung von Nullstellen).
Quellenverweise
[1] J. Feng, A New Two-step Method for Solving Nonlinear
Equations (2009),
International Journal
of Nonlinear Science, Vol.8 (2009) No.1, (40-44)
• Contra Harmonic Newton-Verfahren für komplexe Funktionen
In [1] stellt der Verfasser eine Erweiterung des Newton-Verfahrens vor, das er auf Grund des verwendeten Mittelwertes "Contra Harmonic Newton-Verfahren" nennt (s. auch [2] zum contra-harmonischen Mittelwert). Das zweistufige Verfahren hat für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ die Iterationsvorschrift
und besitzt die Konvergenzordnung q = 3 bei einem Effizienzindex von CE = 1.442.
Quellenverweise
[1] O. Y. Ababneh (2012),
New Newton’s Method with Third-order Convergence for Solving Nonlinear Equations (2012),
International Journal of Mathematical and Computational Sciences, Vol. 6, No. 1, 2012,
https://publications.waset.org/13005/pdf
• Kung-Traub-Verfahren für komplexe Funktionen
Kung und Traub stellten 1974 ein zweistufiges Iterationsverfahren vor mit folgender Iterationsvorschrift für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ:
Mit der Konvergenzordnung q = 4 und dem Effizienzindex CE = 1.587 ist es ein optimales Verfahren.
Quellenverweise
[1] H. T. Kung, J. F. Traub,
(1974), Optimal Order of One-Point and Multipoint Iteration,
Journal of the ACM 21(4), 643-651, DOI: 10.1145/321850.321860
• Fang-Ni-Cheng-Verfahren für komplexe Funktionen
Das von Fang et al. publizierte Verfahren Zweischritt-Verfahren zur Nullstellenbestimmung hat für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ folgende Iterationsvorschrift:
Es besitzt die Konvergenzordnung q = 4 bei einem Effizienzindex CE = 1.414.
Quellenverweise
[1] L. Fang, L. Ni, R. Chen (2013), Three Modified Efficient Iterative Methods for Non-linear Equations,
Mathematical Computation, March 2013, Volume 2, Issue 1, (6-12)
http://www.ivypub.org/MC/paperinfo/3415.shtml
• Rafiq-Rafiullah-Verfahren für komplexe Funktionen
In [1] entwickeln die Autoren ein Zwei-Schritt-Verfahren zur Nullstellenbestimmung ("Algorithmus 2"), das für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ folgende Iterationsvorschrift besitzt:
Das Verfahren besitzt die Konvergenzordnung q = 3 bei einem Effizienzindex CE = 1.316.
Quellenverweise
[1] A. Rafiq, M. Rafiullah (2009), Some multistep iterative methods for solving nonlinear equations,
Computers and Mathematics with Applications, 58(2009),1589–1
https://www.sciencedirect.com/science/article/pii/S0898122109004672
• Chun-Kim II -Verfahren für komplexe Funktionen
Die Verfasser konstruieren in [1] neue Verfahren basierend auf einer geometrischen Herangehensweise, ähnlich wie der mit der Tangente beim Newton-Verfahren und einer Hyperbel beim Halley-Verfahren (s. die dortigen Animationen). Hierbei nehmen sie aber den Krümmungskreis zur Hilfe, der im Punkt (xn | yn) die gleiche Tangente wie die Funktion f besitzt. Die dabei erforderliche zweite Ableitung f '' approximieren sie durch den Differenzenquotienten (s. Differential/Ableitung) und erhalten schliesslich die folgende Iterationsvorschrift für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ :
Das Verfahren besitzt die Konvergenzordnung q = 3, der Effizienzindex beträgt CE = 1.442.
Quellenverweise
[1] C. Chun · Y. I. Kim, Several New Third-Order Iterative Methods for Solving Nonlinear Equations (2010),
Acta Appl. Math. (2010) 109: 1053–1063, DOI 10.1007/s10440-008-9359-3
• Chun-Kim III -Verfahren für komplexe Funktionen
Das hier aufgeführte Verfahren beruht auf dem Chun-Kim I -Verfahren, indem die zweite Ableitung f '' durch den Differenzenquotienten (s. Differential/Ableitung) approximiert wird. Angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ ergibt sich somit die folgende Iterationsvorschrift :
Das Verfahren besitzt die Konvergenzordnung q = 3, der Effizienzindex beträgt CE = 1.442.
Quellenverweise
[1] C. Chun · Y. I. Kim, Several New Third-Order Iterative Methods for Solving Nonlinear Equations (2010),
Acta Appl. Math. (2010) 109: 1053–1063, DOI 10.1007/s10440-008-9359-3
• Weerakoon-Fernando-Verfahren für komplexe Funktionen
Für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ lautet die Iterationsvorschrift des Weerakoon-Fernando-Verfahrens
Für weitere Details, Konvergenzordnung q und Effizienzindex CE siehe Weerakoon-Fernando-Verfahren für reelle Funktionen.
• Sharma-Bahl-Verfahren für komplexe Funktionen
In [1] (Gleichung 16) präsentieren R. Sharma und A. Bahl ein 2-Schritt-Verfahren mit folgender Iterationsvorschrift für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ
Der Zwischenschritt (predictor) beruht hier auf einem mit dem Faktor 2/3 modifizierten Newton-Schritt.
Es handelt sich um ein optimales Verfahren mit der Konvergenzordnung q = 4 und einem Effizienzindex CE = 1.587.
Quellenverweise
[1] R. Sharma, A. Bahl (2015),
An Optimal Fourth Order Iterative Method for Solving Nonlinear Equations and Its Dynamics,
Journal of Complex Analysis, Vol. 2015, Article ID 259167, http://dx.doi.org/10.1155/2015/259167
• Chun-Lee-Neta-Verfahren für komplexe Funktionen
C. Chun, M.Y. Lee und B. Neta leiteten ein Verfahren für die Nullstellenbestimmung her [1] (Gleichung 24), das angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ auf folgender Iterationsvorschrift beruht:
Der Zwischenschritt (predictor) beruht hier - wie auch beim Verfahren von Sharma-Bahl auf einem mit dem Faktor 2/3 modifizierten Newton-Schritt. Das Verfahren hat die Konvergenzordnung q = 4 bei einem Effizienzindex CE = 1.587 und ist somit ein optimales Verfahren.
Quellenverweise
[1] C. Chun, M.
Y. Lee, B. Neta (2012),
On optimal fourth-order iterative methods free from second derivative and their dynamics,
Applied Mathematics and Computation 218 (2012) 6427–6438
• Jarratt-Verfahren für komplexe Funktionen
P. Jarratt stellte 1966 in [1] ein 2-Schritt-Verfahren zur Nullstellenbestimmung einer Funktion f vor mit folgendem Iterationsschema für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ :
Sein Verfahren hat gemäß Kung-Traub die optimale Konvergenz q = 4 und einen Effizienzindex von
CE = 1.587 und ist eines der effizientesten bisher bekannten Verfahren vierter Ordnung.
Da es jedoch eine Variante des Newton-Verfahrens ist, kann die Iteration aufgrund eines Überlaufs abbrechen oder zu einer Divergenz führen, wenn die Ableitung der Funktion an einem Iterationspunkt singulär oder fast singulär ist. Da dies die praktische Anwendung des Verfahrens einschränkt, wurden in der letzten Dekade diverse Anstrengungen unternommen, eine global-konvergente allgemeine Klasse von Jarratt-Verfahren mit der Konvergenzordnung vier zu konstruieren, wie z.B. in [2], [3], [4].
Quellenverweise
[4] R. Behl, V. Kanwar, K. K. Sharma,
Modified optimal families of fourth-order Jarratt's method (2013),
International Journal of Pure and Applied Mathematics, Vol. 84, No. 4, S. 331-343
http://dx.doi.org/10.12732/ijpam.v84i4.3
• Solaiman-Hashim-Verfahren für komplexe Funktionen
Das Verfahren von Solaiman-Hashim hat für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ die folgende Iterationsvorschrift:
Für weitere Details, Konvergenzordnung q und Effizienzindex CE siehe Solaiman-Hashim-Verfahren für reelle Funktionen.
• Ham-Chun-Verfahren für komplexe Funktionen
In [1] stellen die Verfasser ein Iterationsverfahren der Ordnung
q = 5 auf. Für komplexe Funktionen
f : D → ℂ mit D ⊆ ℂ besitzt es die Iterationsvorschrift
Der Effizienzindex des Verfahrens beträgt CE = 1.495.
Quellenverweise
[1] Y. M. Ham, C. Chun (2007) A fifth-order iterative method for
solving nonlinear equations
Applied Mathematics and
Computation 194 (2007) 287–290
• Fang-Sun-He-Verfahren für komplexe Funktionen
Das in [1] vorgestellte Verfahren hat für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ die Iterationsvorschrift
Seine Konvergenzordnung ist q = 5, der Effizienzindex beträgt CE = 1.495.
Quellenverweise
• Ghanbari-Verfahren für komplexe Funktionen
Ausgehend vom Fang-Sun-He-Verfahren (s.o.) entwickelt der Verfasser in [1] eine Familie von Iterationsverfahren, bei der sich durch entsprechende Parametrisierung die zwei folgenden Iterationsvorschriften für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ ergeben:
Verfahren I (Gleichung 9 in [1] )
Verfahren II (Gleichung 10 in [1] )
Beide Verfahren besitzen die Konvergenzordnung q = 5 und den Effizienzindex CE = 1.495.
Quellenverweise
[1] B. Ghanbari (2012) A New Family of Nonlinear Fifth-Order Solvers for Finding Simple Roots
Applied Mathematics, 2012, 3, S. 577-580, http://dx.doi.org/10.4236/am.2012.36088
• Chun-Ham I -Verfahren für komplexe Funktionen
Chun und Ham verwenden in [1] bekannte Iterationsverfahren vierter Ordnung und entwickelt daraus ein neues Verfahren, das für komplexe Funktionen f : D → ℂ mit D ⊆ ℂ die folgende Iterationsvorschrift (Gleichung 9 in [1]) besitzt:
Das Verfahren hat auch die Konvergenzordnung q = 4. Da aber die Ableitung des Predictors f '(wi) eliminiert werden konnte und somit nur 2 Funktionswerte und eine Ableitung pro
Iterationsschritt berechnet werden müssen, beträgt der Effizienzindex CE = 1.587 und ist somit besser als der der ursprünglichen Verfahren.
Quellenverweise
[1] C. Chun, Y. M. Ham (2008) Some fourth-order modifications of Newton’s
method
Applied Mathematics and Computation
197 (2008), S. 654–658
• Ardelean-Verfahren für komplexe Funktionen
Ardelean stellt in [1] sein zweistufiges Verfahren vor, das er "Bisectrix Newton Method" nennt und das, wie er sagt, auf "geometrischen Beobachtungen" basiert. Das Prinzip des Verfahrens zeigt die folgende Animation am Beispiel einer reellen Funktion f.
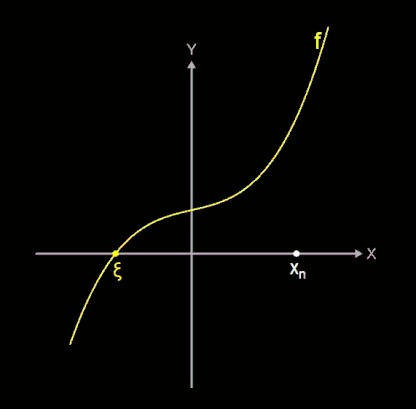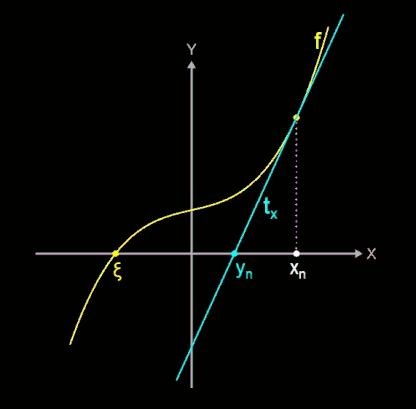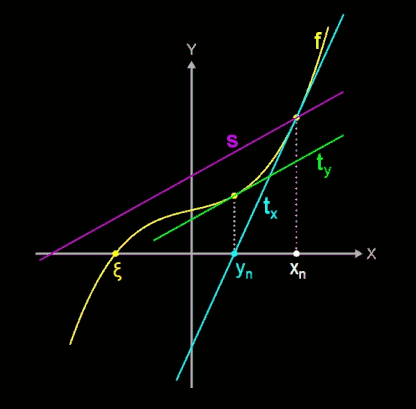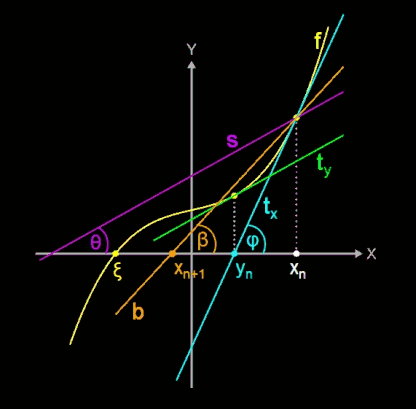
Sei xn ein Näherungswert an eine einfache Nullstelle ξ von f (x) = 0.
- Mit dem Newton-Verfahren und der Tangente tx an f in f (xn) ergibt sich zunächst ein Zwischenwert yn.
- Dann bilde man die Tangente ty an f in f (yn).
- Eine Parallelverschiebung von ty ergibt die Gerade s, die durch f (xn) verläuft.
- Nun bilde man die Winkelhalbierende b (engl. bisectrix) des Winkels zwischen ty und s.
- Diese schneidet die x-Achse im Punkt xn+1 und ergibt so den nächsten Näherungswert.
Zur Herleitung der Iterationsvorschrift betrachte man den Winkel β, den die Winkelhalbierende b mit der x-Achse bildet. Für diesen gilt:
Es ist
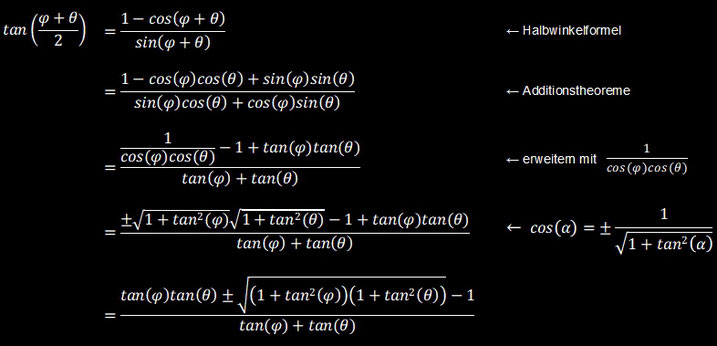
Einsetzen in die obige Iterationsgleichung ergibt:
Für die Winkel φ und θ, die tx und s mit der y-Achse bilden, gilt: tan (φ) = f ' (xn), tan (θ) = f ' (yn).
Somit ergibt sich das fertige Iterationsverfahren zu
bzw. angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ zu:
Das Verfahren besitzt die Konvergenzordnung q = 3 und den Effizienzindex CE = 1.442.
Quellenverweise
[1] G. Ardelean (2013) A new third-order newton-type iterative method for
solving nonlinear equations,
Applied Mathematics and Computation 219 (2013), S. 9856–9864
http://dx.doi.org/10.1016/j.amc.2013.03.131
• Kou-Li-Liu-He-Verfahren für komplexe Funktionen
Auf der Basis einer Variante des Halley-Verfahrens und mit Ersetzen der zweiten Ableitung f '' durch den Differentialquotienten entwickeln die Verfasser in [1] neue Iterationsverfahren, im folgenden angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ.
Verfahren I (Gleichung 9 in [1])
Verfahren II (Gleichung 11 in [1])
Beide Verfahren besitzen die Konvergenzordnung q = 3. Der entscheidende Vorteil gegenüber dem Newton-Verfahren und vielen anderen, die auf dem Newton-Verfahren basieren, ist der, dass die Bedingung f ' (z) ≠ 0 entfällt. Gegenüber diesen Verfahren sind die beiden Verfahren in vielen Fällen vorzuziehen, insbesondere dann, wenn keine ausreichend guten Anfangsnäherungen an die gesuchte Nullstelle bereitgestellt werden oder die erste Ableitung f ' in einer Umgebung der gesuchten Nullstelle kleine Werte annimmt oder sogar gleich Null ist.
Quellenverweise
[1]
J. Kou, Y. Li, D. Liu, J. He (2007) Third-order iterative methods free from second derivative,
International Mathematical Forum, 2, 2007, no. 14, S. 689 - 698
• Chun-Ham II -Verfahren für komplexe Funktionen
Die Verfasser leiten in [1] eine Familie von Iterationsverfahren vierter Ordnung mit dem Parameter λ ∈ ℝ (Gleichung 15 in [1]) her - im folgenden angewandt auf komplexe Funktionen f : D → ℂ mit D ⊆ ℂ :
Das Verfahren benötigt keine zweite Ableitung, der Effizienzindex beträgt CE = 1.587.
Quellenverweise
• Kou-Li-Verfahren für komplexe Funktionen
Indem sie beim Chebyshev-Verfahren die zweite Ableitung durch eine finite Differenz der Ableitungen ersetzen, leiten die Verfasser eine Familie von Verfahren ohne die zweite Ableitung von f her:
Durch entsprechende Wahl des Parameters θ erhält man einerseits bereits bekannte Verfahren, aber auch neue, wobei die Verfasser insbesondere die Fälle θ = (√5 – 1 ) / 2 und θ = -2 favorisieren. Sie zeigen, dass alle Verfahren dieser Falilie die Konvergenzordnung q = 3 besitzen.
Quellenverweise
[1] J. Kou, Y. Li (2011) Modified Chebyshev’s method free from second derivative for non-linear equations,
Applied Mathematics and Computation 187 (2007) 1027–1032, doi:10.1016/j.amc.2006.09.021
• Chun-Neta-Verfahren für komplexe Funktionen
Die Verfasser wenden die Methode der unbestimmten Koeffizienten auf das Newton-Verfahren an und erhalten so unter anderem ein Verfahren (Gleichung 34) mit der Konvergenzordnung q = 3:
Quellenverweise
[1] C. Chun, B. Neta (2009) Certain improvements of Newton’s method with fourth-order convergence,
Applied Mathematics and Computation 215 (2009), S. 821–828, doi:10.1016/j.amc.2009.06.007
