Iterative Verfahren zur Nullstellenbestimmung

Um die Nullstelle(n) einer (stückweise) stetigen Funktion f zu bestimmen - also die Gleichung f (x) = 0 zu lösen - bietet sich, falls alle anderen Methoden (s. Nullstellen Grundlagen) "versagen", eine numerische Lösung mit iterativen Verfahren an.

Bei solch einem Verfahren / Algorithmus wird - ausgehend von einem oder mehreren Startpunkten (in der Nähe der vermuteten Nullstelle) - eine Iteration durchgeführt, die im günstigen Fall (nach einigen wenigen Schritten) gegen die Nullstelle konvergiert, d.h. dass das Abbruchkriterium | x_i – x_i-1 | < ε für eine gewünschte Genauigkeit ε erfüllt ist.

Im Allgemeinen kann nicht garantiert werden, dass ein Algorithmus zur Nullstellenbestimmung alle Nullstellen einer Funktion findet. Falls dieser also keine Nullstelle findet, bedeutet dies nicht, dass keine Nullstelle existiert.

Wünschenswert wäre natürlich ein Algorithmus, der für jeden Startwert x₀ (oder für eine Kombination mehrerer Startwerte wie z.B. beim Tiruneh-Verfahren), stets und mit möglichst wenigen Iterationsschritten zur Nullstelle ξ konvergiert, d.h. dass für jede Folge {x_i} gilt:

Leider existiert solch ein "Super-Algorithmus" nicht. Neben konstruktionsbedingten Einschränkungen (z.B. versagt das Newton-Verfahren, falls die Ableitung für einen Wert x_i der Iterationsfolge 0 wird) kann die Effizienz eines Algorithmus dramatisch von den Eigenschaften der gegebenen Funktion und von der Wahl der Startwerte abhängen.

Konvergenzordnung

Ein wichtiges Maß zur Beurteilung der Leistungsfähigkeit eines Algorithmus ist die Konvergenzordnung (auch Konvergenzgeschwindigkeit).

Ein Verfahren konvergiert linear, falls gilt:

Je kleiner die Konvergenzrate c ist, desto schneller konvergiert die Folge {x_i} gegen die Nullstelle ξ.

Ist c = 0, spricht man von superlinearer Konvergenz. Um superlineare Konvergenzraten zu unterscheiden, führt man folgende Definition ein:

Falls für die Folge {x_i} gilt:

dann konvergiert sie mit der Ordnung q gegen ξ für q > 1.

Hierbei muss q keine natürliche Zahl sein (z.B. ist q beim Sekantenverfahren die "Goldene Zahl" φ = 1.618 … des Goldenen Schnitts). Ist q = 2, so liegt quadratische Konvergenz vor (z.B. beim Newton-Verfahren), bei q = 3 spricht man von kubischer Konvergenzordnung (z.B. Tiruneh-Verfahren), etc.

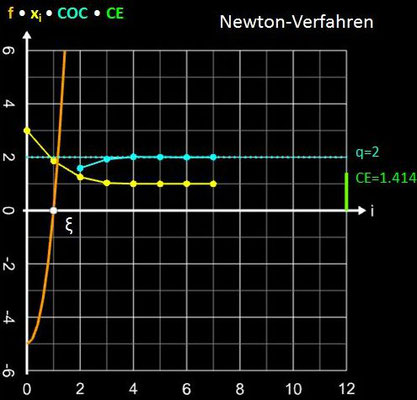
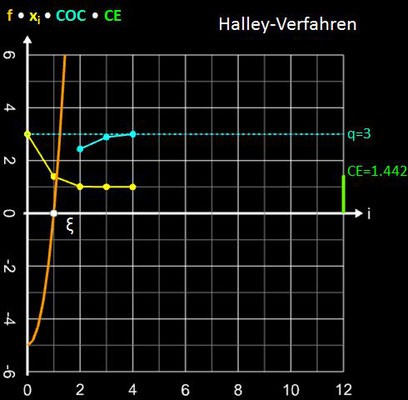
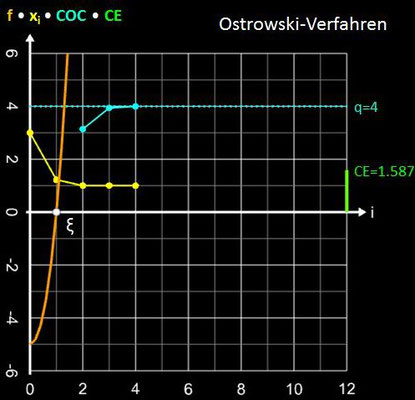
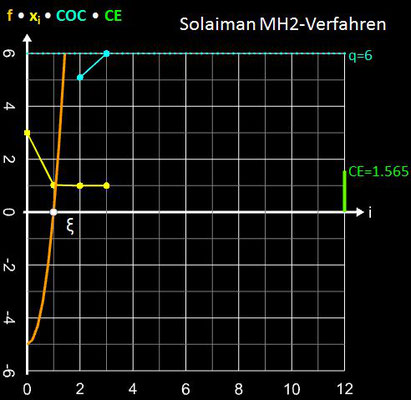
Eine praktische Methode, um die Konvergenzordnung für ein Verfahrens (Folge) zu bestimmen, ist die Berechnung der folgenden Sequenz dreier aufeinanderfolgender Glieder, die gegen q konvergiert und die mit COC (engl. Computational Order of Convergence) bezeichnet wird:

Die Diagramme in der folgenden Galerie zeigen dies für einige Verfahren mit der Funktion f (x) = x³ + 4x² - 5 mit der positiven Nullstelle ξ = 1, dem Startwert x₀ = 3 (für Sekanten- und Tiruneh-Verfahren d = 0.1) und dem Abbruchkriterium | x_i – x_i-1 | + | f (x_i) | ≤ 10^-15.

Sekantenverfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3, d=0.1

Newton-Verfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3

Tiruneh-Verfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3, d=0.1

Halley-Verfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3

Ostrowski-Verfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3

Solaiman MH2-Verfahren Konvergenzverhalten für x³+4x²-5 und x<sub>0</sub>=3

Effizienz-Index

Ein weiteres Maß bei iterativen Verfahren ist die Effizienz CE (engl. Computational Efficiency), die von J. F. Traub eingeführt wurde [10, S. 260-264]:

wobei q die Konvergenzordnung des Verfahrens (s.o.) ist und m die Anzahl erforderlicher Berechnungen des/der Funktionswert(s) und - abhängig vom Verfahren - der Werte der Ableitung(en) pro Iterationsschritt.

So beträgt z.B. die Effizienz beim Sekantenverfahren (1 Funktionsberechnung: m = 1) CE = 1.6185, beim Newtonverfahren (1 Funktionsberechnung, 1 Berechnung der Ableitung: m = 2) ist CE = √2 ≈ 1.4142.

Konstruktion Iterativer Verfahren zur Nullstellenbestimmung

Das "klassische" Sekanten- und auch Newton-Verfahren zur Nullstellenbestimmung führen in manchen Fällen zu Problemen, wie z.B. sehr langsame Konvergenz, Divergenz, Oszillation und Sprünge (aus dem Bereich der gesuchten Nullstelle heraus); das Newton-Verfahren wird "abgewürgt", falls die Ableitung im Iterationspunkt den Wert 0 annimmt.

Angesichts dieser Problemfälle wurden - interessanterweise viele in den letzten 20 Jahren - vielfältige Modifikationen und Ersatzmethoden, meist "Hybride" aus verschiedenen Methoden, entwickelt und publiziert. Dabei lag das Ziel insbesondere auf der Erhöhung der Konvergenzordnung q, zusätzlich soll aber die Effizienz CE (s.o.) möglichst hoch sein.

Ein weiteres Optimierungsziel bei der Konstruktion eines Algorithmus besteht im Verzicht auf die Ableitung oder zumindest auf höhere Ableitungen (das Aufstellen dieser kann sehr aufwendig sein), um dadurch m zu verringern. Die Ableitungen werden durch geeignete Approximationen ersetzt.

Aus der großen Vielzahl von Publikationen habe ich nur einige wenige mit neueren Verfahren unten unter Links exemplarisch zusammengestellt. In den Publikationen finden Sie in den dortigen Referenzen weitere typische Verfahren.

Einige Verfahren werden auf meiner Webseite auf eigenen Unterseiten näher betrachtet:

Weitere Verfahren werden kurz und mit Beispielen vorgestellt unter Diverse Verfahren.

Unter Verfahrensvergleich finden Sie u.a. eine Positionierung aller betrachteten Verfahren hinsichtlich ihrer Effizienz und der Konvergenzordnung sowie ausgewählte weitere Beispiele.

Links

[1] Trevor J. McDougalla, Simon J. Wotherspoonb (2013), A simple modification of Newton’s method to
achieve convergence of order 1 + √2, Applied Mathematics Letters 29 (2014) 20–25,
http://dx.doi.org/10.1016/j.aml.2013.10.008

[2]   Gustavo Fernández-Torres (2015), A Novel Geometric Modification to the Newton-Secant Method
       to Achieve Convergence of Order 1 + √2 and Its Dynamics, Modelling and Simulation in Engineering
       Volume 2015, http://dx.doi.org/10.1155/2015/502854

[3]   Ababu Teklemariam Tiruneh et al. (2013), A Two-Point Newton Method Suitable for Nonconvergent
       Cases and with Super-Quadratic Convergence, Advances in Numerical Analysis, Volume 2013,
       http://dx.doi.org/10.1155/2013/687382

[4] S. Weerakoon, T. G. I. Fernandao (1998), A Variant of Newton’s Method with Accelerated Third-Order
Convergence, Applied Mathematics Letters 13 (2000), 87-93

[5]   Manoj Kumar, Akhilesh Kumar Singh, Akanksha Srivastava (2013), Various Newton-type iterative
       methods for solving nonlinear equations, Journal of the Egyptian Mathematical Society (2013) 21,
       334–339, http://dx.doi.org/10.1016/j.joems.2013.03.001

[6]   Mehdi Salimia, Taher Lotby, Somayeh Sharibz, Stefan Siegmund (2014), Optimal Newton-Secant like
       methods without memory for solving nonlinear equations,
       https://www.researchgate.net/publication/259360127

[7]   Obadah Said Solaiman, Ishak Hashim (2018), Two new efficient sixth order iterative methods for
       solving nonlinear equations, Journal of King Saud University – Science,
       https://doi.org/10.1016/j.jksus.2018.03.021

[8] Iin Purnama Edwar, M. Imran, Leli Deswita (2016), A Sixth-Order Derivative-Free Iterative Method for
Solving Nonlinear Equations, Bulletin of Mathematics, Vol. 08, No. 01 (2016), pp. 1–8

[9]   Muhammad Raullah, Muhammad Haleem (2010), Three-Step Iterative Method with Sixth Order
       Convergence for Solving Nonlinear Equations, Int. Journal of Math. Analysis, Vol. 4, 2010, no. 50,
       2459 - 2463

[10] J. F. Traub (1964), Iterative Methods for the Solution of Equations, Prentice-Hall, Englewood Cliffs, N. J.