Volumen eines Rotationskörpers mit parametrischer Funktion
Im Folgenden werden Rotationskörper betrachtet, die durch Rotation einer Funktion in parametrischer Darstellung mit x = fx (t), y = fy (t) für x zwischen a und b bzw. für
t in den Grenzen ta und tb entstehen.
Mit
ta = fx-1 (a) tb = fx-1 (b)
ergibt sich [1]:
Rotation um die x-Achse:
Rotation um die y-Achse:
Beispiele für Rotation um die x-Achse
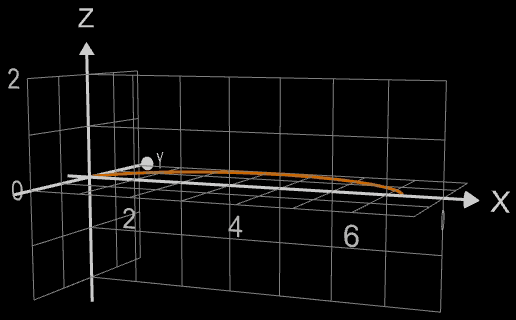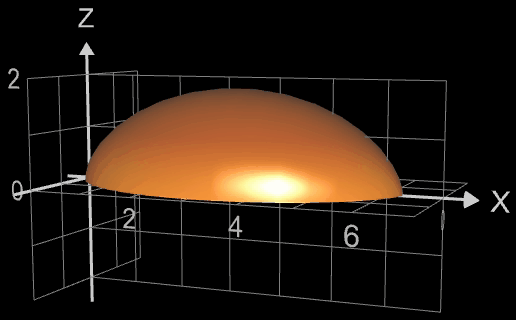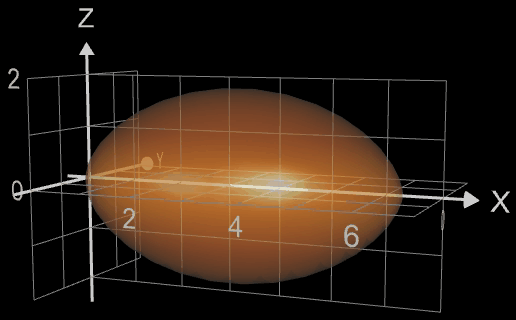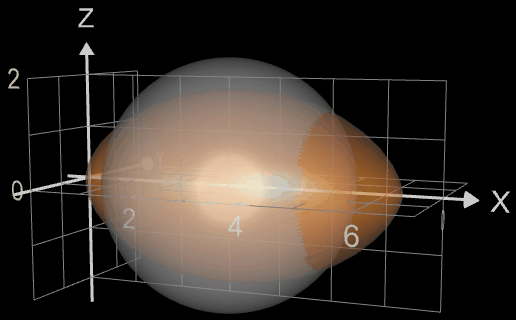
Die Funktion x = fx (t) = t² und y = fy (t) = t - t³ / 3 rotiert um die x-Achse. In der x/y-Ebene hat ihr Graph die Form eines gestreckten "α" (s. Grafik).
Das Volumen des entstehenden "Tropfens" zwischen
a = 0 und b = 3 soll bestimmt werden:
a = 0 = t² → ta = 0
b = 3 = t² → tb = √3
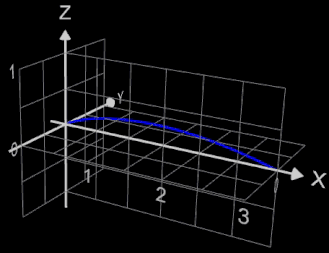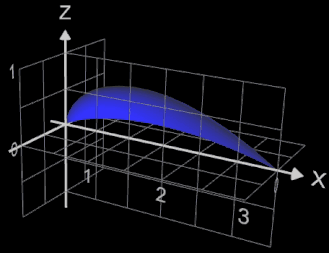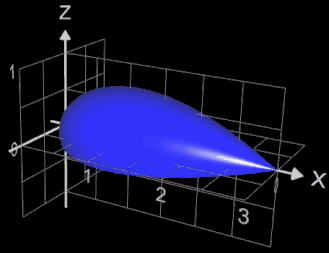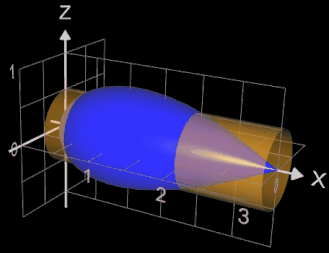
Der braune, transparente Zylinder in der Grafik besitzt bei gleicher "Länge" (b - a = 3) das identische Volumen. Mit seinem Radius von 0.5 hat er die gleichen Maße wie der Zylinder, der der gleichen Mantelfläche des Rotationskörpers entspricht (s. auch Mantelfläche).
Für eine numerische Lösung mit dem Graphing Calculator 3D steht im Donwload-Bereich unten auf der Seite eine gc3-Datei zur Verfügung.
Für das Beispiel ergibt sich eine Genauigkeit von 12 Nachkommastellen.
Der oberhalb der x-Achse liegende Teil einer Kardioide (s. linke Grafik) rotiert um die x-Achse. Das Volumen des Rotationskörpers ist zu bestimmen.
Die parametrische Funktion der Kardiode lautet hier
x = fx (t) = (1 - cos (t) ) cos
(t)
y = fy (t) = (1 - cos (t) ) sin (t)
mit t zwischen - π und 0.


Mit fx ' (t) = - sin (t) + 2 cos (t) sin(t) ergibt sich das Volumen V gemäß
Auch hier liefert der Graphing Calculator 3D mit der Datei im Download-Bereich das Ergebnis auf 12 Nachkommastellen genau.
Das Volumen eines American Footballs (s. folgende linke Abbildung, Quelle: www.amazon.de) soll berechnet werden. Als Randfunktion für den Rotationskörper habe ich eine in y-Richtung mit dem Faktor 0.9 gestauchte Zykloide (s. mittlere Abbildung) gewählt, die dem Aussehen des echten Balls recht nahe kommt:
x = fx (t) = t - sin
(t)
y = fy (t) = 0.9 ( 1 - cos
(t) ) mit t = 0 ... 2π
(braun gefärbter Anteil in mittlerer Grafik)
Für das Volumen gilt:
Die Länge von 2π des Modells entspricht einer echten Länge von ca. 28 cm [2]. Somit ist das berechnete Volumen noch mit dem Faktor (28 / 2π)³ zu multiplizieren, was ein tatsächliches Volumen von 3537 cm³ ergibt. Ein kreisrunder Ball mit gleichem Volumen (weiß, halbtransparent in obiger rechter Abbildung) ist somit etwas kleiner als ein Volleyball.
Beispiele für Rotation um die y-Achse
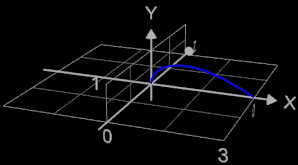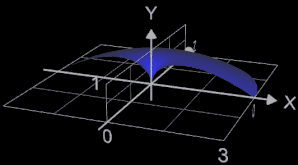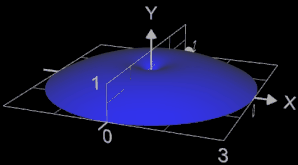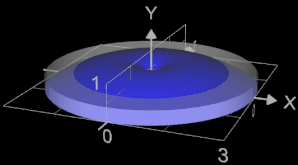
Für die Funktion x = fx (t) = t² y = fy (t) = t - t³ / 3 zu Anfang der Seite ergibt sich das Volumen mit t = 0 ... √3 bei Rotation um die y-Achse (blau in Grafik) wie folgt:
Der Wert des Volumens ist negativ, da parametrische Gleichungen die Kurve/Fläche gegen den Uhrzeiger durchlaufen und somit, abhängig von der gewählten Parametrisierung, beim Integrieren einen negativen Wert liefern (orientiertes Volumen). Das echte Maß des Volumens ist der absolute Wert.
Der graue Zylinder in der Grafik ist hat das gleiche Volumen wie der Rotationskörper.

Für eine Kugel mit dem Radius r ist das Volumen eines Kugelsegments der Höhe h zu bestimmen, wobei die Kugel als Rotationskörper einer parametrischen Funktion um die y-Achse erzeugt werden soll.
x = fx (t) = r sin (t)
y = fy (t) = r cos (t)
mit t = - π / 2 ... π / 2
fy (t) = r cos (t) = r - h
→ ta = acos (1 - h / r)
fy (t) = r cos (t) =
r → tb = acos (1) = 0
Anmerkung: Wesentlich "eleganter" lässt sich das Volumen des Kugelsegments bestimmen, wenn dieses
durch die Rotation einer nichtparametrischen Funktion um die x- Achse entsteht
(s. Volumen Rotation x-Achse):
Das Volumen der Kuppel eines Zwiebelturms (s. Beispiel: Basilius-Kathedrale in Moskau) soll bestimmt werden.
Als Funktion für die Kuppel diene die Funktion
x = fx (t) = 3 cos 4 (t)
y = fy (t) = 5 sin (t) + 1
die mit t = asin (-0.2) ...
π / 2 eine Kuppel der Höhe 5 mit maximalem Radius von 3 erzeugt.
Für das Volumen ergibt sich:
Quellen
[1] Sharma, A. K. (2005), Application Of Integral Calculus, Discovery Publishing House, S.168
[2] https://de.wikipedia.org/wiki/Football_(Sportger%C3%A4t)
Download