3D Galton-Brett

Zur Demonstration und Veranschaulichung der Binomialverteilung [1] entwickelte Sir Francis C. Galton (*1822  †1911) eine Anordnung, die man als Galton-Brett [2] bezeichnet: auf einem Brett sind in regelmäßigen horizontalen Reihen Stifte angebracht. Diese sind in aufeinander folgenden Reihen auf Lücke gesetzt.

Lässt man nun aus einem oben in der Mitte angebrachten Trichter Kugeln (ihr Durchmesser ist etwas kleiner als der freie Abstand zwischen den Stiften) über dieses Brett rollen, entscheidet sich an jedem dieser Stifte mit einer Wahrscheinlichkeit von p=0.5, ob die Kugel nach rechts oder links rollt. Am unteren Ende des Brettes befinden sich mehrere Behälter, in denen sich die Kugeln sammeln.

Führt man dieses Experiment mit einer genügend großen Anzahl von Kugeln durch, lässt sich beobachten, dass sich die meisten Kugeln im mittleren Behälter sammeln, während die äußeren Behälter die geringste Anzahl von Kugeln enthalten. Die Verteilung der Kugeln in den Behältern entspricht einer Binomialverteilung.

Im folgenden Video, das mit Graphing Calculator 3D erstellt wurde (Details nachfolgend),  fallen 50 Kugeln über das Brett (dreifache Wiedergabegeschwindigkeit).

Die Idee ist es, das Abrollen einer Kugel auf dem Galton-Brett zeitlich in einer Animation darzustellen. Wie auch bei anderen Animationen (s. 3D Türme von Hanoi, 3D Sanduhr, 3D Zahnrad, 3D Kugelbahn) wird eine Variable t automatisch inkrementiert. Die Position einer Kugel wird dann entsprechend dem Wert von t berechnet. Im Beispiel oben besteht ein vollständiger Durchlauf der Kugel aus 13 Positionen.

Befindet sich die Kugel über einem der Stifte (t = 2, 4, 6, 8), wird im nächsten Schritt per Zufall ein zufälliger Faktor (-1 oder 1) berechnet mittels

(-1) ^{round (rand)}

 der dann die seitliche Verschiebung (-1: "links", 1: "rechts") bestimmt.

Hierbei tritt jedoch ein Problem auf: bei jeder Inkrementierung durch die Animation der Zeitvariablen t  wird die Funktionenliste vollständig durchlaufen / ausgeführt; dabei werden alle Zufallszahlen für die Richtungsänderung der Kugel auf ihrem Weg neu gesetzt. Dies darf aber nicht sein, da die Position einer Kugel zu irgendeinem Zeitpunkt t_i  von allen vorherigen Zeitpunkten t_i-1 , t_i-2 , t_i-3 , ...  und somit dem bis dato zufällig zurückgelegten Weg abhängt!

Abhilfe bringt es hier, die in Graphing Calculator 3D vorhandene Zufallsfunktion rand durch einen Pseudo-Zufallszahlen-Generator zu ersetzen (s. Diverse Themen/Pseudo-Zufallszahlen). Dieser erzeugt, abhängig von einem einstellbaren Startwert, stets eine gleiche Sequenz von "Zufallszahlen".

Die Graphing Calculator 3D-Datei Galton 4 Rows.gc3 erzeugt die im obigen Video gezeigte Simulation mit maximal 75 Kugeln. Die Anzahl der Kugeln in den Auffangbehältern wird als Balkendiagramm unterhalb des Spielfeldes angezeigt, die tatsächlichen Werte können natürlich auch in der Funktionenliste (H0 bis H4) abgelesen werden.

Die Wahrscheinlichkeit b_n,p (k) beim Galton-Brett mit n Reihen und n+1 Behältern, dass eine Kugel in den Behälter k (k = 0, ..., n) fällt, beträgt auf Grund der Binomialverteilung

Da p = 0.5 beträgt, ergibt sich für das hier dargestellte Galton-Brett mit n = 4 Reihen, k Behältern (k = 0, ..., 4) folglich

und somit für die Behälter 0 bis 4 die folgende prozentuale Verteilung:
b (0) = 6.25 %,  b (1) = 25 %,  b (2) = 37.5 %,  b (3) = 25 %,  b (4) = 6.25 %.

Die folgenden Diagramme zeigen typische Verteilungen für 50, 500 und 5000 Kugeln, wobei die gelben Linien die ideale Binomialverteilung anzeigen.

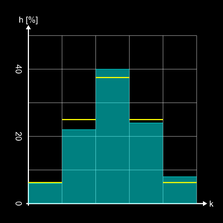
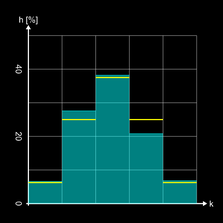
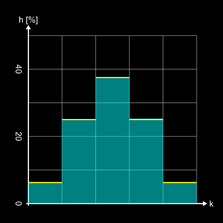
Mit der Graphing Calculator 3D-Datei Galton 4 Rows Analysis.gc3 können die obigen Diagramme für verschiedene Werte von n berechnet werden. Der Zufallsprozess (Fallen einer Kugel durch das Brett) ist der gleiche wie bei obiger 3D-Simulation, jedoch ohne Anzeige des Bretts und des Kugelverlaufs - das würde einfach zu lange dauern  ;-)

Quellen

[1]   http://www.mathepedia.de/Binomialverteilung.aspx

[2]   https://de.wikipedia.org/wiki/Galtonbrett

Download