3D Rotation um beliebige Achse
Soll ein 3D-Objekt/Fläche um eine beliebige Achse im Raum gedreht werden, ist der "Aufwand" deutlich größer.
Die Rotationsachse sei definiert als Gerade durch zwei Punkte P und Q. Mit dem Rotationswnkel δ ergibt sich die Rotation zu
Eine anschauliche Herleitung sowie die Erklärung der Winkel α und β findet man bei [1] und [2].
Rx , Ry und Rz sind die in Rotationen um Koordinatensystem-Achsen beschriebenen Rotationsmatrizen, die inversen Matrizen lauten
Umgesetzt habe ich dies in der Graphing Calculator 3D-Datei Rotation about Arbitrary Axis.gc3. Folgende Eingabemöglichkeiten sind vorgesehen:
- Eingabe der parametrischen Objektfunktion f
- Translation (tx, ty, tz ) und/oder Rotation (αx , αy und αz) des Objekts zur gewünschten Raumposition
- Festlegen der Rotationsachse mit Hilfe der Punkte P und Q
- Drehung des Objekts um den Winkel δ
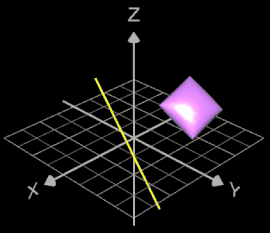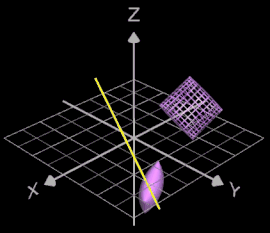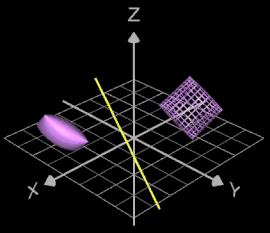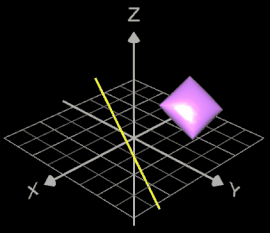
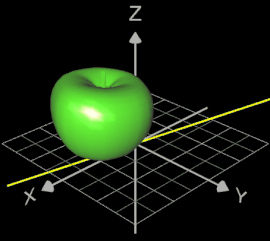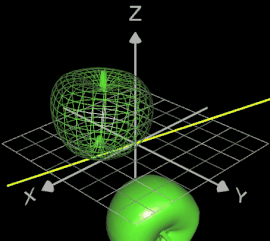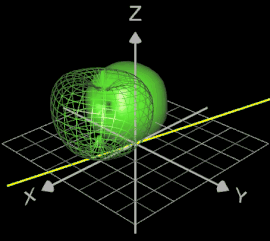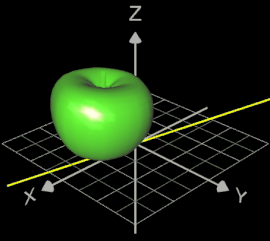
Wird das Objekt gedreht, erscheint es zusätzlich als Drahtgittermodell an der Anfangsposition vor Beginn der Drehung: