Fläche zwischen Funktionen
Eine weitere Anwendung für Integrale ist die Berechnung der Fläche zwischen den Funktionsgraphen zweier Funktionen f und g in einem Intervall [a, b]:
wobei x1,
x2, ..., xn die x-Koordinaten möglicher Schnittpunkte von f und g im Intervall [a, b] sind mit
a < x1 < x2 < ... < xn < b.
Im Falle, dass sich die Graphen im Intervall [a, b] schneiden, kann diese Aufgabe sehr "elegant" mittels Numerischer Integration gelöst werden ohne die Schnittpunkte ermitteln zu müssen :
Die Graphing Calculator 3D-Datei Area between 2 Functions.gc3 zeigt ein Beispiel mit den Funktionen f (x) = 4 sin (0.5 x) (orangener Graph) und g(x) = - sin (x) (blauer Graph). Wieder wird eine numerische Integration durchgeführt, jedoch mit der Hilfsfunktion h (x) = | f(x)-g(x) |:
Programmier-Details
-
Die Einfärbung der Fläche zwischen f und g ist etwas "trickreich": hier wird das Feature von GC3D ausgenutzt, Ungleichungen der Art "y<" and "y>" darstellen zu können zusammen mit geeigneten Fallunterscheidungen.
Die zu berechnende Fläche im Intervall [a, b] ergibt sich dann als Mix aus den Farben (blau und orange) der Ungleichungen.
- Mit der Variablen "show" kann man schnell die Einfärbung der Fläche abschalten.
- Eine andere (einfachere) Lösung zum Einfärben der Fläche A ist in der GC3D-Datei Area between 2 Functions – inv area.gc3 realisiert.Dort ist die zu brechnende Fläche "leer" (Hintergrundfarbe des Plots) während die komplette xy-Fläche im Intervall [a, b] weiß eingefärbt ist:
Fläche zwischen Funktionen - Beispiele
Beispiel 1
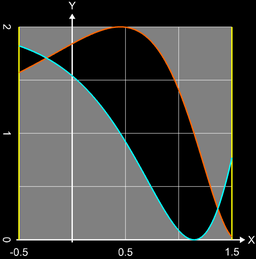
Es soll die Fläche zwischen den Funktionen
im Intervall [-0.5, 1.5] bestimmt werden.
Wollte man dies manuell lösen, so ergäben sich Probleme, denn die Bestimmung der Schnittpunkte und das Herleiten der Stammfunktionen ist alles andere als trivial.
Berechnet man die x-Werte der Schnittpunkte numerisch (z.B. mit dem Sekantenverfahren)
x1 = -0.24156447527049052
x2 = 1.36787343716361
sowie auch die 6 Integrale für die drei Teilbereiche (mit N = 1000) und berechnet die Geamtsumme der Teilflächen, so ist der absolute Fehler gegenüber der "schnellen" Lösung mit der Datei Area between 2 Functions.gc3 kleiner als 10-9.
Beispiel 2
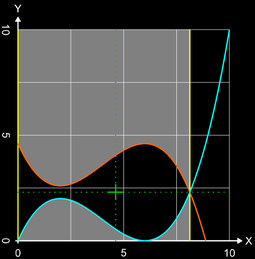
Ein Schild in Form eines stilisierten Fisches soll drehbar auf einem Dach montiert werden. Der "Fisch" wird erzeugt durch die Randfunktionen
f (x) = - 0.0625 x³ + 0.75 x² - 2.25 x + 4.6
g (x) = - f (x) + 4.6
im Intervall [0, 8.13]; hierbei entspricht eine Zeichen-einheit 10 cm. Das Schild ist 4 mm dick, das verwendete Aluminium hat dieDichte ρ = 2.6 g/cm³.
Wie schwer ist das Schild?
Da beide Funktionen Polynome vm Grad 3 sind und dies auch für die Differenzfunktion f (x) - g(x) gilt:
liefert Graphing Calculator 3D die Lösung von A = 20.838867... bereits nach einer Iteration (da die Stammfunktionen zu f ung g existieren, kann die Lösung natürlich auch manuell bestimmt werden).
Das Gewicht G berechnet sich dann zu
G = A • 10² cm² • 0.04 cm • 2.6 g/cm³ ≈ 217 g
Beispiel 3
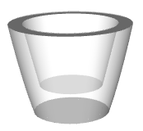
Für einen Rotationskörper (s. Abbildung rechts), der durch Rotation der Funktionen
um die x-Achse eines Koordinatensystems entsteht,
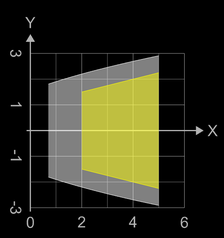
soll die Querschnittsfläche (grauer Bereich in der Abbildung rechts unten) berechnet werden.
Die Berechnung erfolgt in zwei Schritten:
- Wand: f und g mit 0.7 ≤ x ≤ 5
- Boden: f und g (x) = 0 mit 2 ≤ x ≤ 5.
Die Ergebnisse sind dann zu addieren und mit 2 zu multiplizieren. Bei der Berechnung mit GC3D ergibt sich bereits mit N = 50 ein absoluter Fehler kleiner als 10-8 im Vergleich zum exakten Ergebnis von 9.406...
Hinweis:
Da die Stammfunktion für die Differenzfunktion von f und g existiert:
kann die Berechnung des Querschnitts natürlich auch ohne numerische Integration erfolgen.