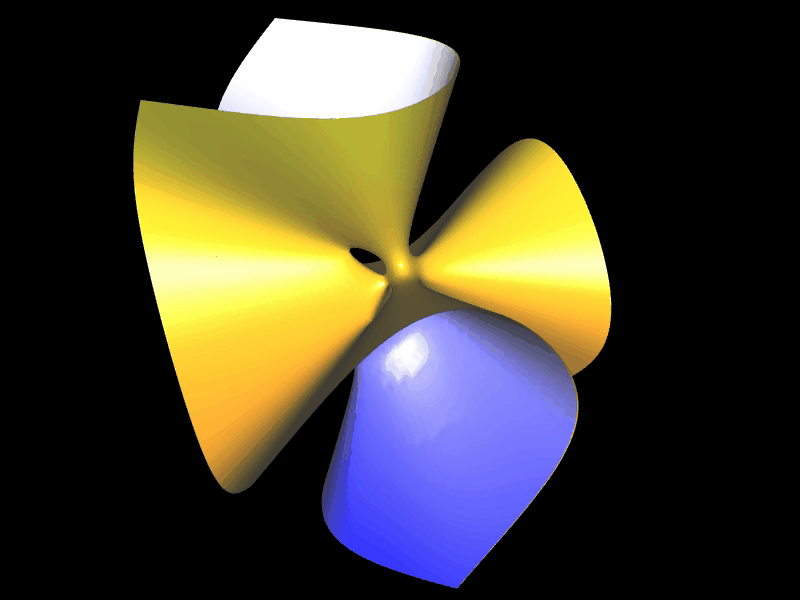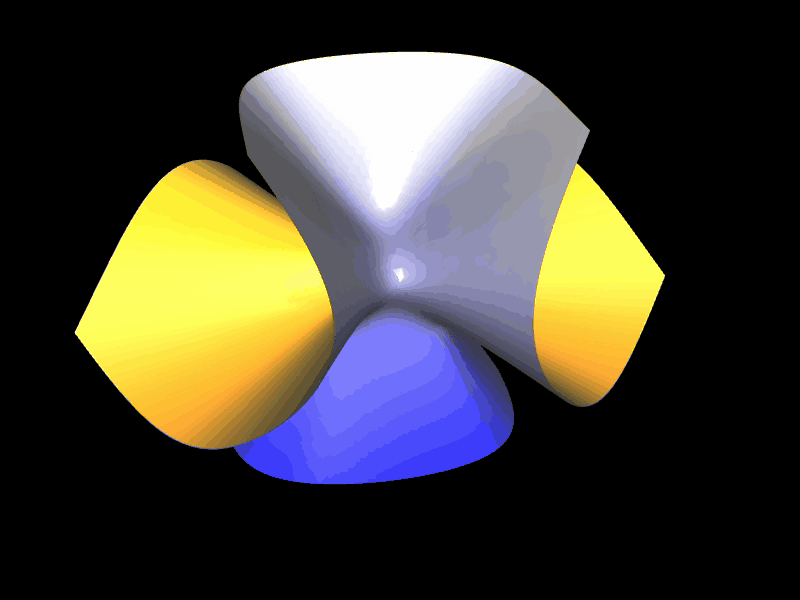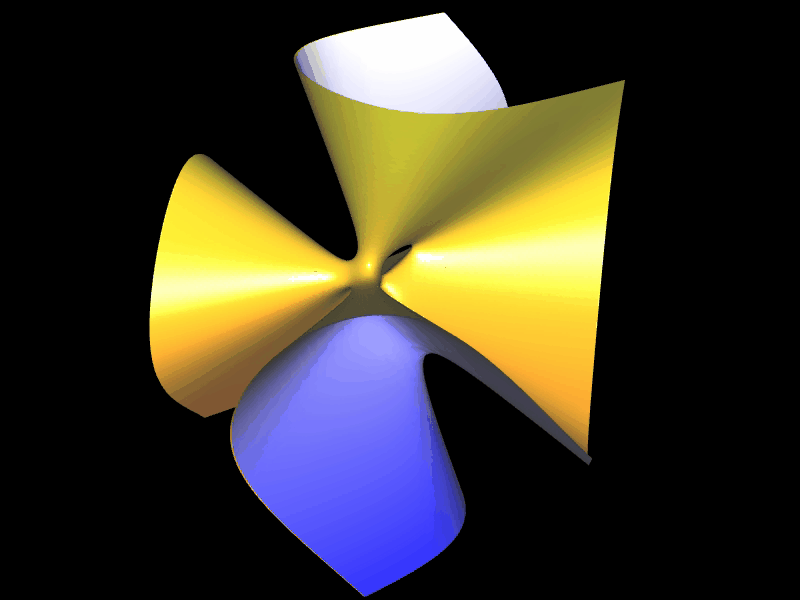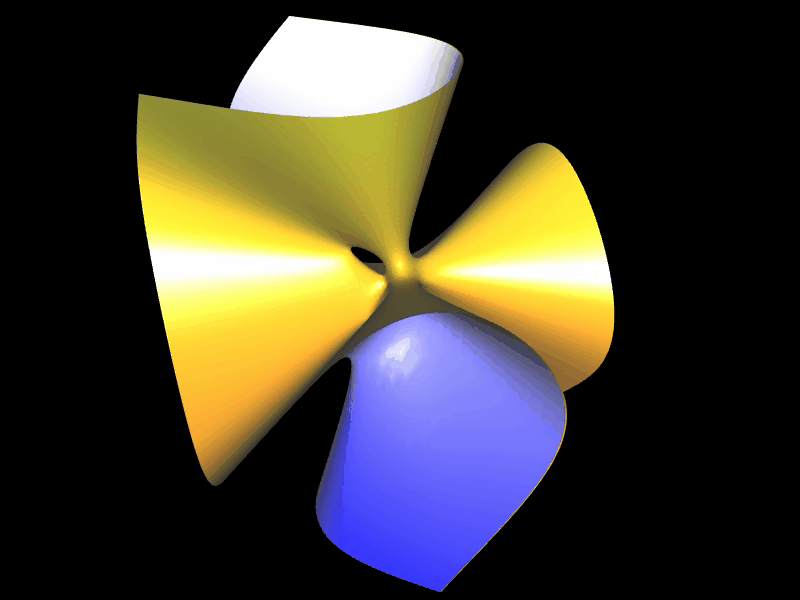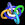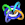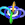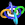Implizite Flächen
Eine implizite Fläche im euklidischen Raum wird durch eine Gleichung der Form f (x, y, z) = 0 beschrieben. Somit besteht eine implizite Fläche A aus der Gesamtheit der Nullstellen einer Funktion von drei Variablen:
A = { (x | y | z) | f (x, y, z) = 0 }.
Implizit bedeutet hierbei, dass die Gleichung der Fläche nicht nach x oder y oder z aufgelöst ist.
Beispiele impliziter Flächen (s. Grafiken unten):
- Ebene: a x + b y + c z + d = 0
- Kugel: x² + y² + z² + r² = 0 r: Radius
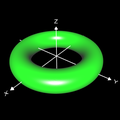
- Torus: (x² + y² + z² + R² - r² )² - 4 R² (x² + y² ) = 0 R: großer Radius, r: kleiner Radius
- Doppeltorus: ((x² + y²)² - x² + y²)² + z² - 0.01 = 0 Fläche vom Geschlecht 2
- Rotationsfläche: x² + y² + sin ² (z) - 1 = 0
Ist f (x, y, z) ein Polynom in x, y und z, so nennt man die zugehörige implizite Fläche algebraisch (spezielle algebraische Flächen werden unter Algebraische Flächen mit Singularitäten betrachtet).
Da das Berechnen der Flächenpunkte (d.h. der Nullstellen von f) wesentlich aufwendiger ist als bei Funktionen in expliziter Darstellung oder bei Parameterflächen, erhöht sich die Rechenzeit, insbesondere für höhere Auflösungen, recht deutlich.
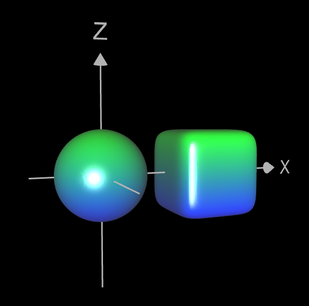
Durch eine implizite Gleichung können im Gegensatz zu Parameterflächen gleichzeitig mehrere implizite Flächen
f1, f2, …, fn definiert werden, indem die Funktionsterme
multipliziert werden:
(s. auch weiter unten unter Vereinigung).
Ist beispielsweise
f1 = x² + y² + z² -1 (Kugel mit Radius 1)
f2 = ((x-2.5)6+y6+z6 -1 ("Würfel" mit Kantenlänge 2)
und
(x² + y² + z² -1) • (((x-2.5)6+y6+z6 -1) =
0
dann liegt ein Punkt p, der diese Gleichung erfüllt, entweder auf der Kugel oder dem "Würfel".
Operationen auf impliziten Flächen
Im folgenden werden einige Operationen auf impliziten Flächen gezeigt, die insbesondere bei der Modellierung von Objekten mit impliziten Flächen
zum Tragen kommen.
Vereinigung und Durchschnitt impliziter Flächen
Die Vereinigung ∪
und der Durchschnitt ∩
sind mengentheoretische Operationen, die es ermöglichen, mehrere implizite Flächen zusammenzufassen. Sind n implizite Flächen definiert durch die Funktionen
f1, f2, …, fn, dann gilt
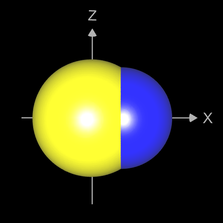
So ergibt beispielsweise für zwei Kugeln f1 (x,y,z) = x² + y² + z² - 4 (gelb in folgender Abbildung) und
f2 (x,y,z) = (x-1)² + y² + z² - 3 (blau)
- min (x² + y² + z² - 4, (x-1)² + y² + z² - 3) = 0 die Vereinigung (grüne Fläche)
- max (x² + y² + z² - 4, (x-1)² + y² + z² - 3) = 0 den Durchschnitt (orangene Fläche).
Die Vereinigung impliziter Flächen wird auch durch Multiplizieren der Funktionsterme erreicht. Für das obige Beispiel ergibt sich die grüne Fläche ebenso mit ((x² + y² + z² - 4) • ((x-1)² + y² + z² - 3)) = 0.
Verschmelzen impliziter Flächen
Mit der Operation Vereinigung erreicht man nicht, dass z.B. zwei Flächen f1 und f2 glatt ineinander übergehen (s. oben). Eine Möglichkeit, um einen glatten Überang zu realisiren, besteht darin, vom Produkt der Funktionsterme eine kleine Zahl a mit 0 < a < 1 zu subtrahieren.
Für die beiden Kugeln oben ergibt sich beispielsweise mit a = 0.01 die gelbe Fläche in der folgenden Abbildung.
Als weiteres Beispiel zeigen die beiden nächsten Grafiken die Verschmelzung zweier Zylinder
x² + y²- 0.5 = 0 (weiß) und y² + z² - 0.5 = 0 (blau). Mit (x² + y²- 0.5) • (y² + z² - 0.5) - 0.1 = 0 ergibt sich dann die Verschmelzung (orange). Je kleiner der Wert von a ist, desto geringer ist
die Verschmelzung.
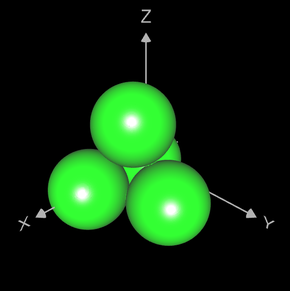
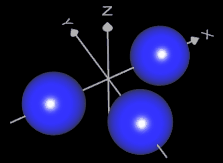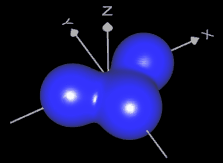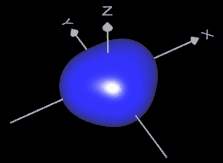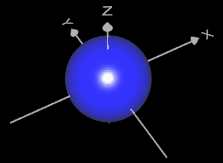
Hier noch ein Beispiel mit mehreren Teilflächen. Die folgende linke Grafik zeigt vier Kugeln mit dem Radius 1 gemäß (x²+y²+z²-1) • ((x-2)²+y²+z²-1) • ((x-1)²+(y-√3)²+z²-1) • ((x-1)²+(y-√3/3)²+(z-2/3•√6)²-1) = 0.
Mit z.B. a = 1 ergibt sich die Verschmelzung in der rechten Grafik gemäß
(x²+y²+z²-1) • ((x-2)²+y²+z²-1) • ((x-1)²+(y-√3)²+z²-1) • ((x-1)²+(y-√3/3)²+(z-2/3•√6)²-1) - 1 = 0.
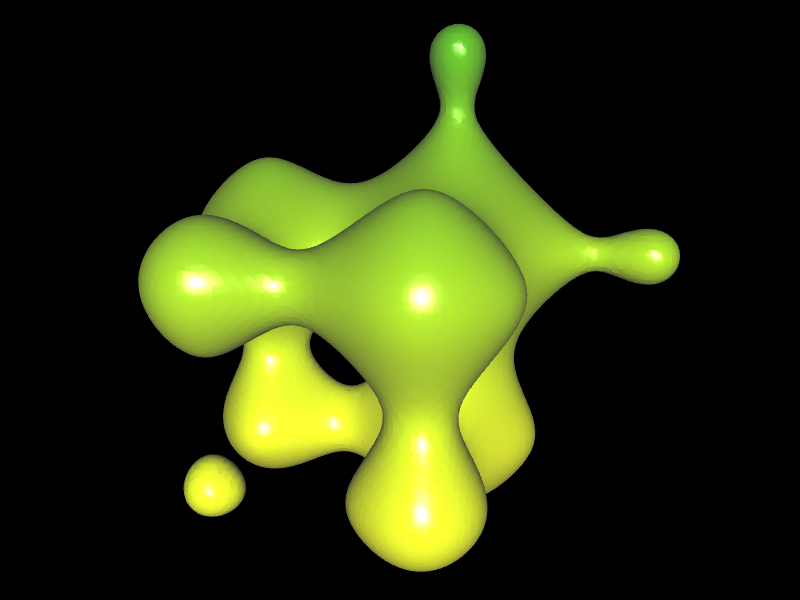
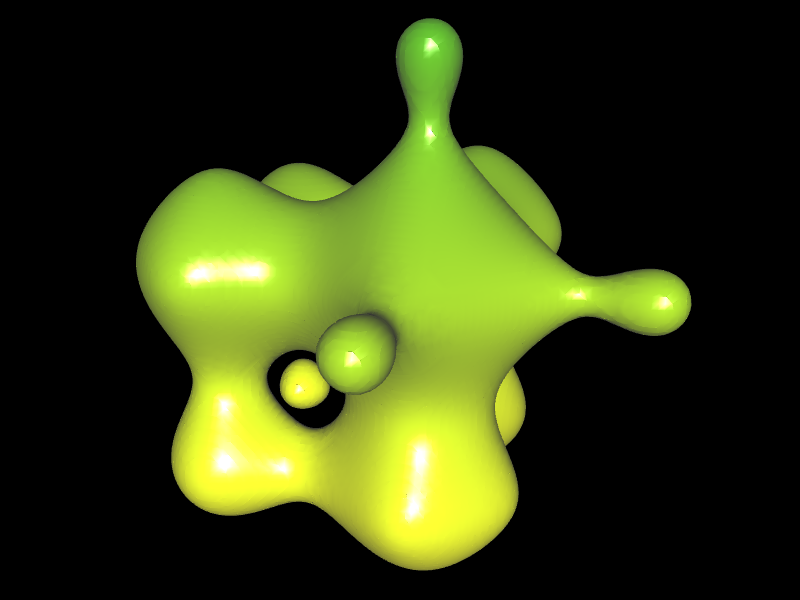
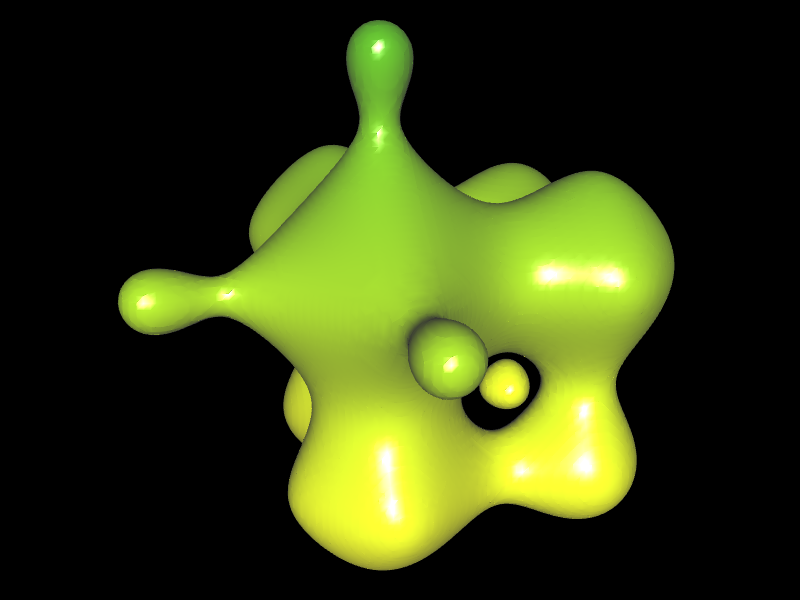
In der Animation bewegen sich drei Kugeln mit Radius 1 aufeinander zu und verschmelzen. Dies passiert z.B. wenn man ein Quecksilberkügelchen an ein anderes heranschiebt: berühren sich beide, verschmelzen sie innerhalb von Sekundenbruchteilen, um für das vorhandene Volumen die Form mit der kleinsten Oberfläche zu bilden: eine Kugel.
Allerdings haben Quecksilberkugeln trotz der hohen Oberflächenspannung auf Grund ihres Gewichtes eine eher linsenartige Form (s. Foto, Quelle: www.paracelsus-magazin.ch). In der folgenden Animation habe ich die zuvor beschriebene Situation einmal simuliert.
Interpolation impliziter Flächen
Zwei implizite Flächen f1 und f2, können interpoliert werden, indem man die mit einem Faktor gewichteten Funktionsterme addiert. Wählt man z.B. einen Parameter c mit 0 ≤ c ≤ 1 und
c • f1 (x ,y, z) + (1 - c ) • f2 (x ,y, z) = 0
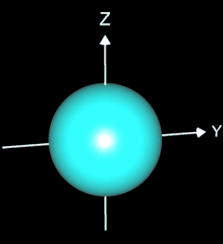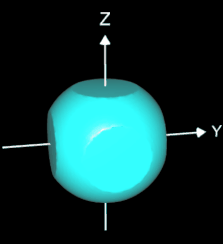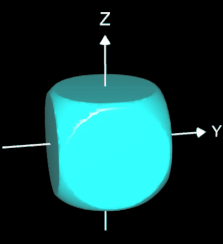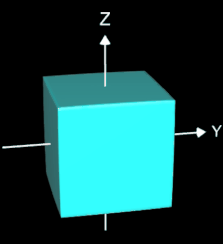
so entspricht die entstehende Fläche für c = 1 der Fläche f1, für c = 0 der Fläche f2; für Werte von c zwischen 0 und 1 entsteht eine interpolierte Fläche. So kann man z.B. ein Morphing zwischen einer Kugel und einem Würfel realisieren, indem man c animiert. (s. blaue Fläche in der folgenden Abbildung).
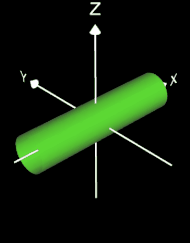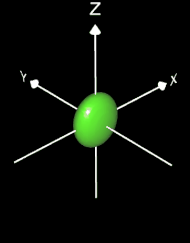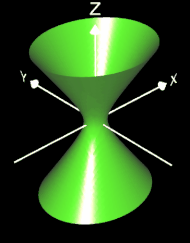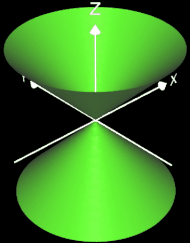
Die grüne Fläche zeigt die Interpolation eines Kegels und eines Zylinders in x-Richung.
Mit Hilfe der Interpolation können auch eher "ungewöhnliche" Flächen realisiert werden. So entsteht die orangene Fläche in der folgenden Abbildung durch die Interpolation der Flächen f1 und f2, mit a = 0.4 und
f1 (x, y, z) = x² + y² - z² (Kegel)
f2
(x, y, z) = (x-1)100 + y100 + z100 -
1 (um +1 in x-Richtung
versetzter Würfel).
Die oben betrachteten Operationen kamen u.a. zum Einsatz bei der Modellierung der 3D Objekte 3D Birne, 3D Tiere, 3D Pilz, 3D Mond unter 3D Mathe / 3D Objekte.
Schnittkurve impliziter Flächen
Die Schnittkurve zweier impliziter Funktionen f1 und f2 (eine unendlich dünne Linie) errechnet sich gemäß
f1 (x, y, z) ² + f2 (x, y, z) ² - d = 0.
Um die Schnittkurve sichtbar zu machen, muss die Dicke der Linie d etwas größer als 0 gewählt werden. Die rote Fläche in der folgenden linken und mittleren Grafik zeigt die Schnittlinie zweier zueinander rechtwinkling angeordneter, sich schneidender Zylinder mit a = 0.00001. Im rechten Bild ist diese Schnittlinie für a = 0.001 in blau dargestellt.
Implizite Flächen - Galerie
In dieser Galerie habe ich einige interessante Implizite Flächen zusammengestellt. Diese wurden alle mit dem Graphing Calculator 3D (s. auch Tools) erzeugt. Hierfür steht dort der Graph Type Implicit zur Verfügung.
In der Tabelle unten auf der Seite finden Sie für die einzelnen Flächen die zugehörigen Funktionsgleichungen in einer kopierbaren Notation, die die meisten Mathematikprogramme verarbeiten können, sowie die Parametereinstellungen. Auf Wunsch schicke ich auch gerne entsprechende Graphing Calculator 3D-Dateien per Mail zu - kontaktieren Sie mich dazu einfach.
Bei den meisten Flächen gibt es mehrere Ansichten. Verwenden
Sie die Steuerelemente
oder klicken Sie auf die Miniaturansicht, um sich gezielt ein Bild anzuschauen.
Insbesondere lohnt sich eine vergrößerte, detailreichere
Ansicht durch Klicken auf das Symbol .
Sine Surface (Sinus Fläche) aus 2, 4 impliziten Teilflächen
Schnitt Barth Sextic (30 cusps) mit Kugel
Verschmelzen Barth Sextic
(30 cusps) mit Kugel
Scherk Torus, N=6, t=0
Scherk Torus, N=4, t=1
Scherk Torus, N=12, t=1
... to be continued ...
Implizite Flächen - Tabelle der Funktionen und Parameter
| Fläche | Funktion | x | y | z |
|
Blob
|
x^2+y^2+z^2+sin(4*x)+sin(4*y)+sin(4*z)-1 = 0 |
-π : π |
-π : π |
-π : π |
|
Clebsch Surface
|
f(x,y,z)=81*(x^3+y^3+z^3)-189*(x^2*y+x^2*z+y^2*x+y^2*z+z^2*x+z^2*y)+54*x*y*z
f(x,y,z)=81*(x^3+y^3+z^3)-189*(x^2*y+x^2*z+y^2*x+y^2*z+z^2*x+z^2*y) |
-3 : 3 |
-3 : 3 |
-3 : 3 |
|
Deko-Würfel
|
1 < a < 2 0 < b < 2
((x^2 + y^2 -a^2)^2+(z^2-1)^2) ((y^2 + z^2 -a^2)^2 + (x^2-1)^2) ((z^2 + x^2 -a^2)^2 + (y^2-1)^2) - b = 0 |
-2 : 2 |
-2 : 2 |
-2 : 2 |
|
Icosahedron
|
p=(1+sqrt(5))/2
1-(cos(x+p*y)+cos(x-p*y)+cos(y+p*z)+cos(y-p*z)+cos(z-p*x)+cos(z+p*x)) = 0
x^2+y^2+z^2<=33 |
-7 : 7
|
-7 : 7
|
-7 : 7
|
|
Klein Bottle
|
(x^2+y^2+z^2+2*y-1)*((x^2+y^2+z^2-2*y-1)^2-8*z^2)+16*x*z*(x^2+y^2+z^2-2*y-1) = 0 |
-4 : 4
|
-4 : 4
|
-4 : 4
|
|
Lattice
|
T=1 G=-1 ((cos(x-(-sin(x)*sin(y)+cos(x)*cos(z))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(-sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(y -(-sin(y)*sin(z)+cos(y)*cos(x))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(-sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))+cos(y-(-sin(y)*sin(z)+cos(y)*cos(x))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(z-(-sin(z)*sin(x)+cos(z)*cos(y))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))+cos(z-(-sin(z)*sin(x)+cos(z)*cos(y))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(x-(- sin(x)*sin(y)+cos(x)*cos(z))*T/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2)))) * ( (cos(x-(-sin(x)*sin(y)+cos(x)*cos(z))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+( -sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(y-(-sin(y)*sin(z)+cos(y)*cos(x))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+( -sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))+cos(y-(-sin(y)*sin(z)+cos(y)*cos(x))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(z-(-sin(z)*sin(x)+cos(z)*cos(y))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))+cos(z-(-sin(z)*sin(x)+cos(z)*cos(y))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2))*sin(x-(-sin(x)*sin(y)+cos(x)*cos(z))*G/sqrt((-sin(x)*sin(y)+cos(x)*cos(z))^2+(- sin(y)*sin(z)+cos(y)*cos(x))^2+(-sin(z)*sin(x)+cos(z)*cos(y))^2)))) = 0
x^2 + y ^2 + z ^2 <= 64 |
-8 : 8 |
-8 : 8 |
-8 : 8 |
|
Lidinoid
|
(sin(2x)sin(z)cos(y)+sin(2y)cos(z)sin(x)+sin(2z)cos(x)sin(y)) -(cos(2x)cos(2y)+cos(2y)cos(2z)+cos(2z)cos(2x))+0.3 = 0
a = 2, π, 5, 2π
x^2+y^2+z^2 <= a^2 |
-8 : 8 |
-8 : 8 |
-8 : 8 |
|
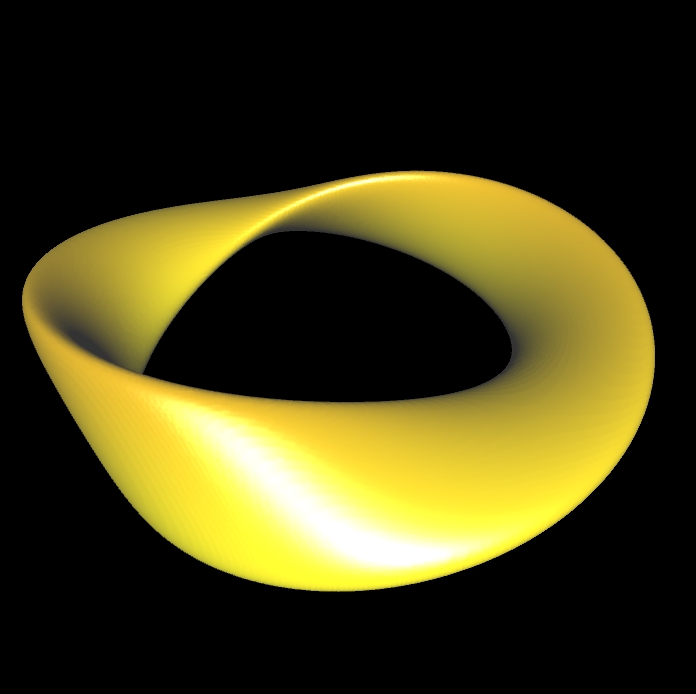
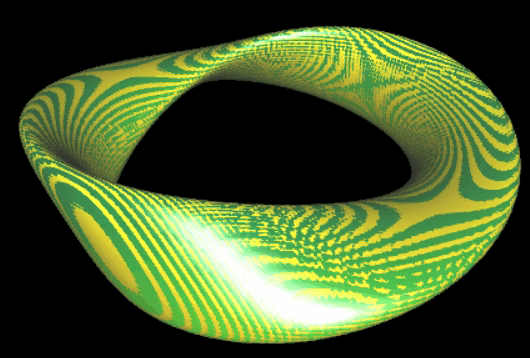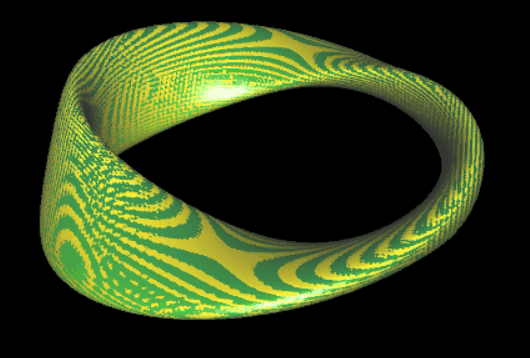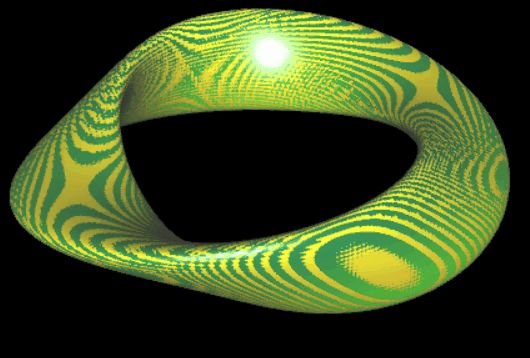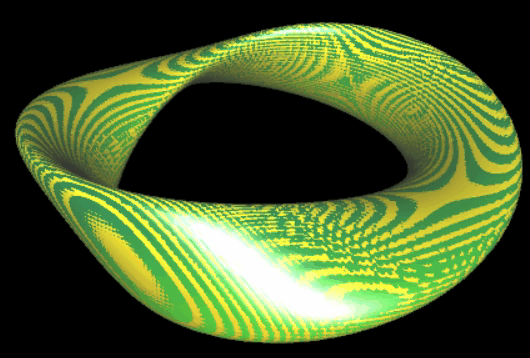
Möbius-Band (räumlich massiv)
|
a = 0.1 b = 0.3
Ausgangspunkt Torus (a=b): (-(a^2+b^2)*(x^2+y^2)+0.5 *(b^2-a^2)*x*(1+x^2+y^2-z^2) -(b^2-a^2)*y*z)^2-(x^2+y^2) *(-0.5*(a^2+b^2) *(1+x^2+y^2+z^2)+a^2*b^2 +(b^2-a^2)*(x-y*z))^2 = 0 1-fach gedreht: (-(a^2+b^2)*(x^2+y^2)+0.5 *(b^2-a^2)*x*(1+x^2+y^2-z^2) -(b^2-a^2)*y*z)^2-(x^2+y^2) *(-0.5*(a^2+b^2) *(1+x^2+y^2+z^2)+a^2*b^2 +(b^2-a^2)*(x-y*z))^2 = 0 2-fach gedreht: ((0.5*(a^2+b^2) *(1+x^2+y^2+z^2)-a^2*b^2) *(x^2+y^2)+0.5*(b^2-a^2) *(x^2-y^2)*(1+x^2+y^2-z^2) -2*(b^2-a^2)*x*y*z)^2 -(x^2+y^2)*((a^2+b^2) *(x^2+y^2)+(b^2-a^2) *(x^2-y^2-2*x*y*z))^2=0 3-fach gedreht: (-(a^2+b^2)*(x^2+y^2)^2+0.5 *(b^2-a^2)*(x^3-3x*y^2) *(1+x^2+y^2-z^2) -(b^2-a^2)*(3x^2y-y^3)*z)^2 -(x^2+y^2)*(-(0.5*(a^2+b^2) *(1+x^2+y^2+z^2)-a^2*b^2) *(x^2+y^2)+(b^2-a^2) *(x^3-3x*y^2 -(3*x^2*y-y^3)*z))^2 =0 4-fach gedreht: ((0.5*(a^2+b^2) *(1+x^2+y^2+z^2)-a^2*b^2) *(x^2+y^2)^2+0.5 *(b^2-a^2) *(x^4-6x^2y^2+y^4) *(1+x^2+y^2-z^2)-3 *(b^2-a^2) *(x^2-y^2)*x*y*z)^2 -(x^2+y^2)*((a^2+b^2) *(x^2+y^2)^2+(b^2-a^2) *(x^4-6*x^2*y^2+y^4-3 *(x^3*y-x*y^3)*z))^2=0 5-fach gedreht: (-(a^2+b^2) *(x^2+y^2)^3+0.5 *(b^2-a^2) *(x^5-10x^3y^2+5x*y^4) *(1+x^2+y^2-z^2)-(b^2-a^2) *(5x^4y-10x^2y^3+y^5)*z)^2 -(x^2+y^2)*(-(0.5*(a^2+b^2) *(1+x^2+y^2+z^2)-a^2*b^2) *(x^2+y^2)^2+(b^2-a^2) *(x^5-10x^3y^2+5x*y^4 -(5x^4y-10x^2y^3+y^5)*z))^2=0 6-fach gedreht: ((0.5*(a^2+b^2)*(1+x^2+y^2+z^2)-a^2*b^2)*(x^2+y^2)^3+0.5*(b^2-a^2) *(x^6-15x^4y^2+15x^2y^4-y^6)*(1+x^2+y^2-z^2)-(b^2-a^2)*(6x^5y-20x^3y^3+6x*y^5) *z)^2-(x^2+y^2)*((a^2+b^2)*(x^2+y^2)^3+(b^2-a^2)*(x^6-15x^4y^2+15x^2y^4-y^6 -(6x^5y-20x^3y^3+6x*y^5)*z))^2 = 0
|
-1.5 : 1.5
|
-1.5 : 1.5
|
-1.5 : 1.5
|
|
Schnitt Barth Sextic
|
1. Fläche - Barth Sextic 30 cusps: PHI = ((1+√5)/2) f(x,y,z) = 4*(PHI^2*x^2-y^2)*(PHI^2*y^2-z^2)*(PHI^2*z^2-x^2)-(1+2*PHI)*(x^2+y^2+z^2-1)^3 2. Fläche - Kugel: g(x,y,z) = x^2+y^2+z^2 - beta
f(x,y,z)^2 + g(x,y,z)^2 - gamma = 0 beta = 2 gamma = 0.045 |
-1.5 : 1.5 |
-1.5 : 1.5 |
-1.5 : 1.5 |
|
Schwarz Double P Surface
|
0.5(cos(x)cos(y)+cos(y)cos(z)+cos(z)cos(x))+0.2(cos(2x)+cos(2y)+cos(2z)) = 0
-π ≤ x, y, z ≤ π bzw. -2π ≤ x, y, z ≤ 2π
|
-8 : 8
|
-8 : 8
|
-8 : 8
|
|
Interpolation Neovius Surface mit Labs Quintic
|
1. Fläche - Neovius Surface: f(x,y,z)=3 (cos(x)+cos(y)+cos(z))+4 (cos(x)*cos(y)*cos(z))
2. Fläche - Labs Quintic: g(x,y,z)=x^5-10*x^3*y^2+5*x*y^4-3*z^5-5*x^4-10*x^2*y^2-5*y^4+10*z^3+20*x^2+20*y^2-15*z-24
x^2+y^2+z^2<=6.5^2
f(x,y,z) + 0.001* g(x,y,z) = 0 |
-7 : 7
|
-7 : 7
|
-7 : 7
|
|
Sine Surface und Oktahemioktaeder
|
a² (x4 + y4 + z4 - 2 (x2y2 + y2z2 + z2x2)) + 4x2y2z2 = 0
x = a sin (u) y = a sin (v) z = a sin (u + v) -π ≤ u, v, z ≤ π |
-1 : 1 |
-1 : 1 |
-1 : 1 |
|
Sine Surface aus 2, 4 impliziten Teilflächen
|
2 Teilflächen: a (x² + y² - z²) ± 2xy √ (a² - z²) = 0
4 Teilflächen: ± x √ (a² - y²) ± y √ (a² - x²) - a z = 0 |
-1 : 1 |
-1 : 1 |
-1 : 1 |
|
Verschmelzen Barth Sextic (30 cusps) mit Kugel
|
1. Fläche - Barth Sextic 30 cusps: PHI = ((1+√5)/2) f(x,y,z) = 4*(PHI^2*x^2-y^2)*(PHI^2*y^2-z^2)*(PHI^2*z^2-x^2)-(1+2*PHI)*(x^2+y^2+z^2-1)^3
2. Fläche - Kugel: g(x,y,z) = x^2+y^2+z^2 - beta
f(x,y,z) * g(x,y,z) + gamma = 0 beta = 1.7 gamma = -0.07
f(x,y,z) * g(x,y,z) + gamma = 0 beta = √1.3 gamma = -0.02
|
-1.5 : 1.5
|
-1.5 : 1.5
|
-1.5 : 1.5
|
|
Interpolation Neovius Surface mit Nordstrand Quartic
|
1. Fläche - Neovius Surface: f(x,y,z)=3 (cos(x)+cos(y)+cos(z))+4 (cos(x)*cos(y)*cos(z))
2. Fläche - Nordstrand Quartic:
g(x,y,z)=25(x^3(y+z)+y^3(x+z)+z^3(x+y))+50(x^2y^2+x^2z^2+y^2z^2)
x^2+y^2+z^2<=8.5^2
f(x,y,z) + 0.0001* g(x,y,z) = 0
|
-7 : 7
|
-7 : 7
|
-7 : 7
|
|
"Chained"
|
██ ((sqrt(x^2+y^2)-3)^2+z^2-2/5)=0 ██ ((sqrt(x^2+y^2)-5)^2+z^2-2/5)=0 ██ ((sqrt((x-9/2)^2+z^2)-3)^2+y^2-2/5)=0 ██ ((sqrt((x+9/2)^2+z^2)-3)^2+y^2-2/5)=0 ██ ((sqrt((x+9/2)^2+z^2)-3)^2+x^2-2/5)=0 ██ ((sqrt((y-9/2)^2+z^2)-3)^2+x^2-2/5)=0
██ ((sqrt(x^2+y^2)-3)^2+z^2-2/5) * ... * ((sqrt((y-9/2)^2+z^2)-3)^2+x^2-2/5)=0
|
-8 : 8 |
-8 : 8 |
-4 : 4 |
|
Torus Distortion
|
t = - 3/2 π ... - 1/2 π
██ z-(15/10)*x*sin(2*t)*exp(-x*x-y*y)-2*y*cos(3*t)*exp(-x*x-y*y)=0
██ (sqrt((x-(15/10)*x*sin(2*t)*exp(-x*x-y*y))^2 + (y-2*y*cos(3*t)*exp(-x*x-y*y))^2)
-1)^2 |
-2 : 2 |
-2 : 2 |
-2 : 2 |
|
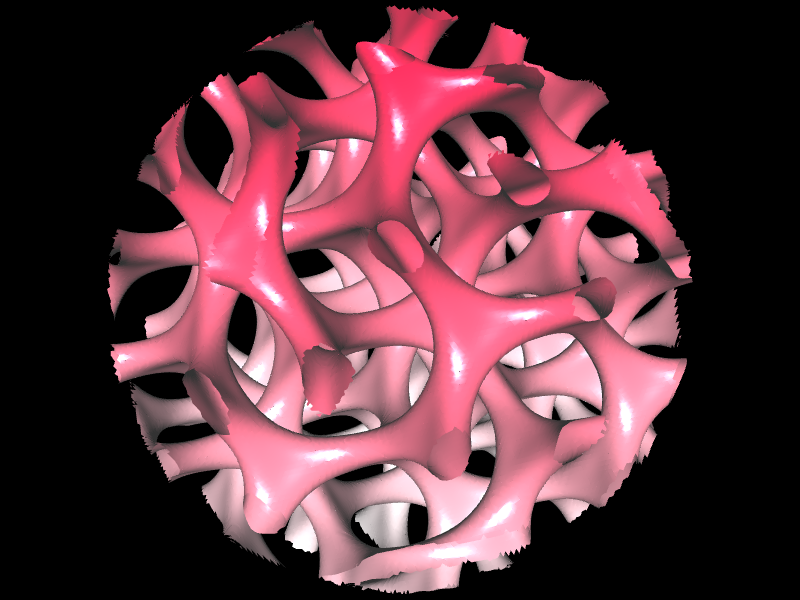
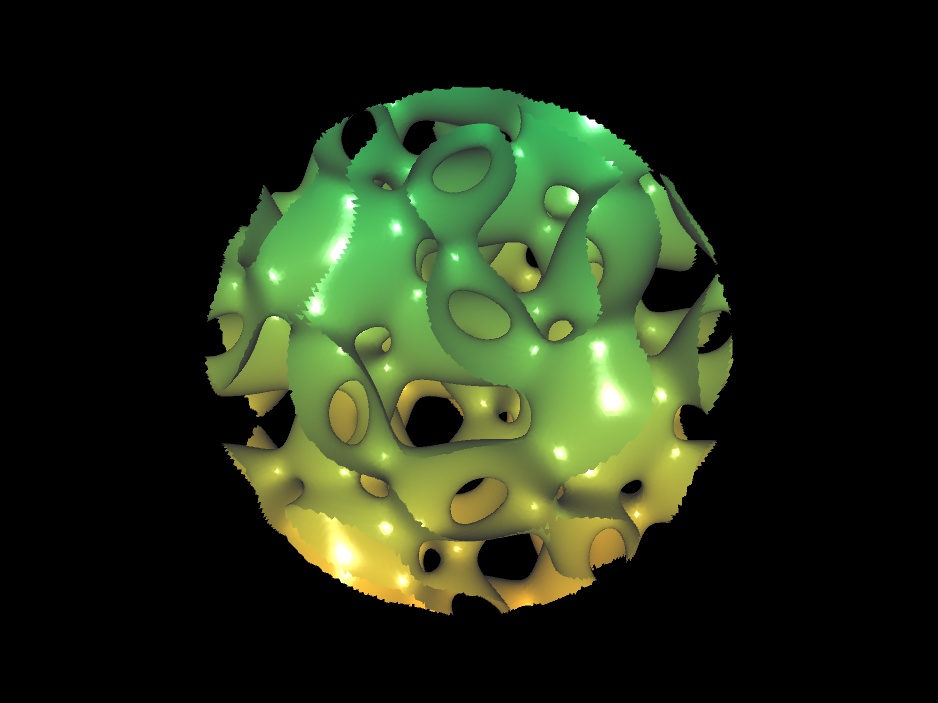
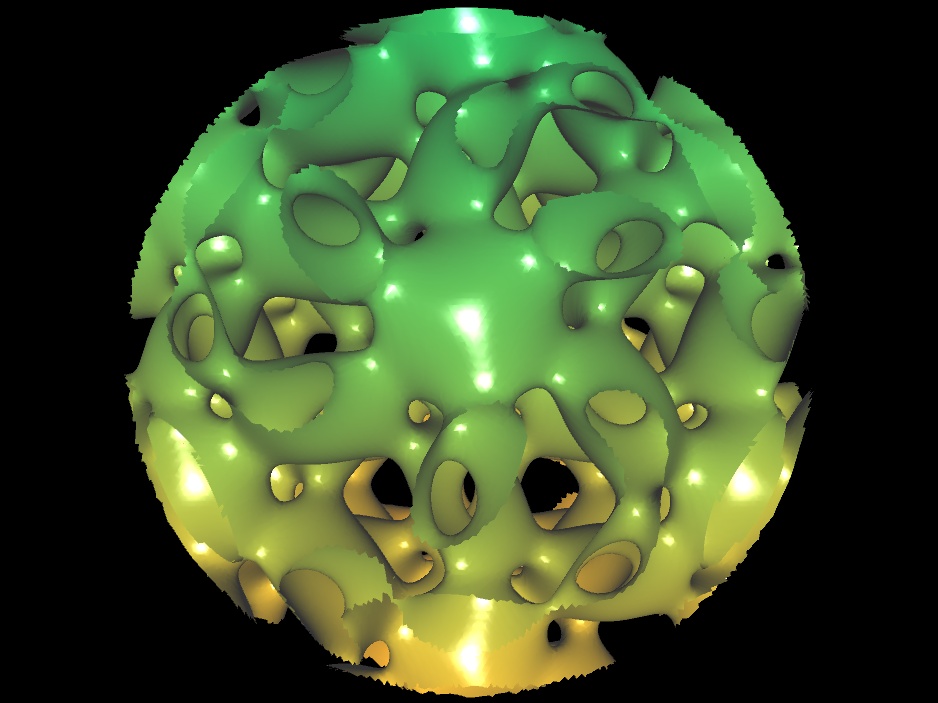
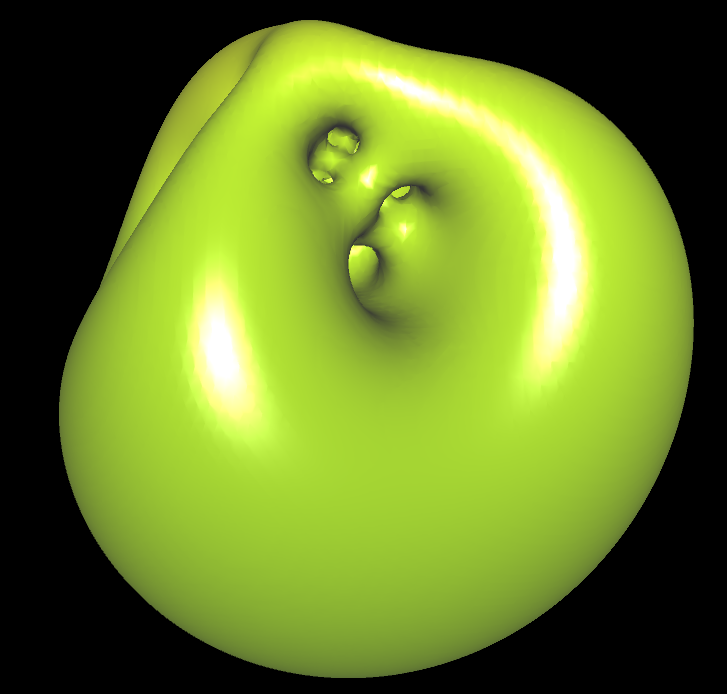
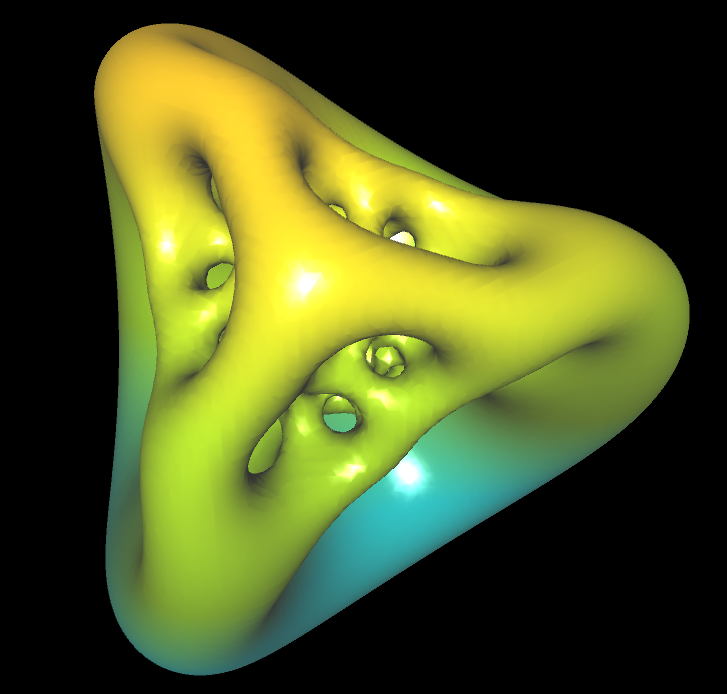
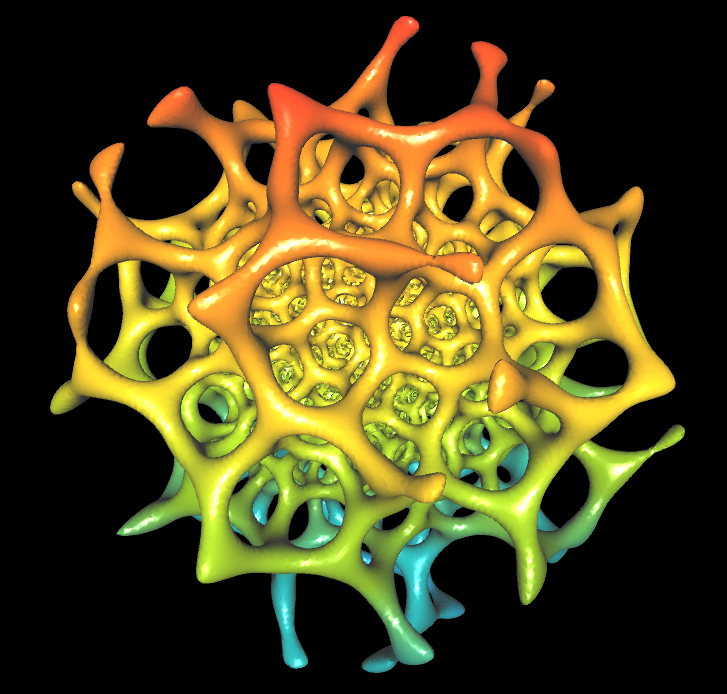
Alien Life Form
|
k=0.4, 1, 2, 3, 4, 12
RR (x,y,z)=k*(x/(x^2+y^2+z^2)) Gyroid(x,y,z)=cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)
Gyroid(RR(x,y,z),RR(y,x,z),RR(z,y,x)) + exp((0.1)*(x^2+y^2+z^2-0.2)) |
-1 : 1 |
-1 : 1 |
-1 : 1 |
|
Scherk Torus
|
N=4, 6, 12 rad=7 t=0, 1
Scherk0(x,y,z) =-((x*y-z)*(x*y-z)-0.4) Scherk1(x,y,z) =Scherk0(sinh(x),sinh(y),sin(z)) ; (abs(x)<3 and abs(y)<3) Scherk1(x,y,z) =0 ; (abs(x)>3 or abs(y)>3) Scherk2(x,y,z,t) =Scherk1(x*cos(t)-y*sin(t),x*sin(t)+y*cos(t),z) Torus(x,y,z,t) = Scherk2( (sqrt(x*x+z*z)-rad), y, N*atan2(z,x),t) |
-10 : 10 |
-10 : 10 |
-10 : 10 |