Parameterflächen
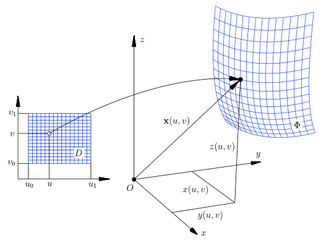
Eine Parameterfläche Φ ist eine zweiparametrige Punktmenge des 3-dimensionalen Raums.
Sie kann daher durch eine Vektor-Funktion zweier Parameter u und v beschrieben werden.
Diese Funktion heißt Parameterdarstellung der Fläche.
Dabei durchlaufen die Paare (u, v) ein gewisses Gebiet D der u,v-Ebene. Dieses Gebiet ist oft rechteckig mit Seiten parallel zur u- und v-Richtung.
In der Abbildung ist D = [u0 , u1] × [v0 , v1].
Quelle: http://geometrie.eduhi.at/data/KS/gfrerrer_kurven-und-flaechen.pdf
Im Gegensatz zu einer Fläche, die sich als Graph einer Funktion mit zwei Veränderlichen f (x, y) ergibt, können einem Punkt (x | y) auch mehrere z-Werte zugeordnet sein, so dass sich Parameterflächen auch ideal zum Modellieren beliebiger 3D Objekte eignen.
Hier einige Basisflächen ...
Kreisscheibe
x = r • v cos (u)
y = r • v sin (u)
z = 0
u = 0 ... 2 π v = 0 ... 1
r: Radius
Zylinder
x = r cos (u)
y = r sin (u)
z = v • h
u = -π ... π v = 0 ... 1
r : Radius h: Höhe
Kegel
x = r v cos (u)
y = r v sin (u)
z = v • h
u = 0 ... 2 π v = 0 ... 1
r: Radius h: Höhe
Ellipsoid
x = a cos (u) sin (v)
y = c sin (u) sin (v)
z = b cos (v)
u = 0 ... 2 π v = 0 ... π
a: große Halbachse
b: kleine Halbachse
c: halbe "z-Dicke"
mit a = b = c : Kugel
Parameterflächen - Galerie
Die Parameterflächen in dieser Galerie wurden alle mit dem Graphing Calculator 3D (s. auch Tools) erzeugt. Hierfür steht der Graph Type Parametric zur Verfügung; das Gebiet D kann mit den Parametern u und v unter Override Default Range eingestellt werden.
In der Tabelle unten auf der Seite finden Sie die zugehörigen Funktionsgleichungen in einer kopierbaren Notation, die die meisten Mathematikprogramme verarbeiten können, sowie die Parametereinstellungen.
Auf Wunsch schicke ich auch gerne entsprechende Graphing Calculator 3D-Dateien per Mail zu - kontaktieren Sie mich dazu einfach.
Bei den meisten Flächen gibt es mehrere Ansichten. Verwenden
Sie die Steuerelemente
oder klicken Sie auf die Miniaturansicht, um sich gezielt ein Bild anzuschauen.
Insbesondere lohnt sich eine vergrößerte, detailreichere
Ansicht durch Klicken auf das Symbol 
.
Parameterflächen - Tabelle der Funktionen und Parameter
| Fläche |
parametrische Funktion (u, v) |
weitere Parameter |
u | v |
|
Boy's Surface
|
x = (sqrt(2)*cos(v)^2*cos(2*u)+cos(u)*sin(2*v))/(2-a*sqrt(2)*sin(3*u)*sin(2*v))
y = (sqrt(2)*cos(v)^2*sin(2*u)-sin(u)*sin(2*v))/(2-a*sqrt(2)*sin(3*u)*sin(2*v))
z = (3*cos(v)^2)/(2-a*sqrt(2)*sin(3*u)*sin(2*v)) |
a = 0 ... 1
a=0: |
0 : π |
0 : π |
|
Boy's Surface
|
x = 0.5((2(cos(u)sin(v))^2-(sin(u)sin(v))^2-(cos(v))^2)((cos(u)sin(v))^2+(sin(u)sin(v))^2 +(cos(v))^2)+2(sin(u)sin(v))(cos(v))((sin(u)sin(v))^2-(cos(v))^2)+(cos(u)sin(v))(cos(v)) ((cos(u)sin(v))^2-(cos(v))^2)+(cos(u)sin(v))(sin(u)sin(v))((sin(u)sin(v))^2-(cos(u)sin(v))^2))
y = 0.5(sqrt(3)(((sin(u)sin(v))^2-(cos(v))^2)((cos(u)sin(v))^2+(sin(u)sin(v))^2+(cos(v))^2) +(cos(v))(cos(u)sin(v))((cos(v))^2-(cos(u)sin(v))^2)+(cos(u)sin(v))(sin(u)sin(v)) ((sin(u)sin(v))^2-(cos(u)sin(v))^2)))
z = 0.125((cos(u)sin(v))+(sin(u)sin(v))+(cos(v)))(((cos(u)sin(v))+(sin(u)sin(v))+(cos(v)))^3 +4((sin(u)sin(v))-(cos(u)sin(v)))((cos(v))-(sin(u)sin(v)))((cos(u)sin(v))-(cos(v)))) |
0 : π |
0 : π |
|
|
Breather
|
x = -u+(2*c2*cosh(c1*u)*sinh(c1*u))/c5(u,v) y = (2*c3*cosh(c1*u)*((-1)*c3*cos(v)*cos(c3*v)-sin(v)*sin(c3*v)))/c5(u,v) z = (2*c3*cosh(c1*u)*((-1)*c3*sin(v)*cos(c3*v)+cos(v)*sin(c3*v)))/c5(u,v)
c2=1-c1^2 c3=sqrt(c2) c5(u,v)=c1*((c3*cosh(c1*u))^2+(c1*sin(c3*v))^2) |
0.4 < c1 < 1 |
-10 : 10 |
-50 : 50 |
|
Bonan Jeener Klein
|
x = a*cos(u)-cos(a*u)-((a-1)/a)(sin((a-1)*u)+b)sin((a+1)*u/2)cos(v) y = (sin((a-1)*u)+b)sin(v) z = a*sin(u)-sin(a*u)+((a-1)/a)(sin((a-1)*u)+b)cos((a+1)*u/2)cos(v)
|
|
0 : 2 π |
0 : 2 π |
|
Crescent
|
x = (2 + sin(2*pi*u)*sin(2*pi*v))*sin(3*pi*v) y = (2 + sin(2*pi*u)*sin(2*pi*v))*cos(3*pi*v) z= cos(2*pi*u)*sin(2*pi*v)+4*v-2 |
0 : 1 |
0 : 1 |
|
|
Dini Surface
|
x = rr*cos(n*u)sin(v) y = rr*sin(n*u)sin(v) z = rr*(cos(v)+ln(tan(v/2)))+b*n*u |
|
0 : 2 π |
0 : 2 |
|
Dupin Cyclide
|
x = (d (c - a cos(u) cos(v)) + b^2 cos(u))/( a - c cos(u) cos(v)) y = (b sin(u) (a - d cos(v)))/( a - c cos(u) cos(v)) z = b sin(v) (c cos(u) - d)/( a - c cos(u) cos(v)) |
|
0 : 2 π |
0 : 2 π |
|
Fresnel Surface
|
x = cos(u)*cos(v)/(-2.*sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4)*cos(v)^4 +sin(v)^4))*cos((acos(-(-0.941/6+0.374*((cos(u)^4+sin(u)^4)*cos(v)^4+sin(v)^4) -1.309/6.*((cos(u)^6+sin(u)^6)*cos(v)^6+sin(v)^6)-1.221*cos(u)^2*cos(v)^4 *sin(u)^2*sin(v)^2)/sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4)*cos(v)^4 +sin(v)^4))^3)-pi)/3.)+0.8)
y = sin(v)/(-2.*sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4)*cos(v)^4+ sin(v)^4))*cos((acos(-(-0.941/6+0.374*((cos(u)^4+sin(u)^4)*cos(v)^4+sin(v)^4) -1.309/6.*((cos(u)^6+sin(u)^6)*cos(v)^6+sin(v)^6)-1.221*cos(u)^2* cos(v)^4*sin(u)^2*sin(v)^2)/sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4) *cos(v)^4+sin(v)^4))^3)-pi)/3.)+0.8)
z = sin(u)*cos(v)/(-2.*sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4)*cos(v)^4 +sin(v)^4))*cos((acos(-(-0.941/6+0.374*((cos(u)^4+sin(u)^4)*cos(v)^4 +sin(v)^4)-1.309/6.*((cos(u)^6+sin(u)^6)*cos(v)^6+sin(v)^6)-1.221 *cos(u)^2*cos(v)^4*sin(u)^2*sin(v)^2)/sqrt(0.965/3.-0.935/3.*((cos(u)^4+sin(u)^4)*cos(v)^4+sin(v)^4))^3)-pi)/3.)+0.8) |
0 : 2 π |
-0.5π : 0.5 π |
|
|
Folium
|
x = 15*cos(u)(2v/pi-tanh(v)) y = 15*cos(u+2pi/3)/cosh(v) z = 15*cos(u-2pi/3)/cosh(v) |
-π : π |
-π : π |
|
|
Hyperbolic Helicoid
|
x = sinh(v)cos(a*u)/(1+cosh(u)cosh(v)) y = sinh(v)sin(a*u)/(1+cosh(u)cosh(v)) z = cosh(v)sinh(u)/(1+cosh(u)cosh(v)) |
a = 4 |
-4 : 4 |
-4 : 4 |
|
Jeener Klein Surface
|
x = a*cos(u)+cos(a*u)-(((a+1)/4)cos((a+1)u+pi/b)+sqrt(c))sin((a-1)u/2)cos(v)
y = (((a+1)/4)cos((a+1)u+pi/b)+sqrt(c))sin(v)
z = a*sin(u)-sin(a*u)-(((a+1)/4)cos((a+1)u+pi/b)+sqrt(c))cos((a-1)u/2)cos(v) |
|
0 : 2 π |
0 : 2 π |
|
Klein Bottle
|
x = 6*cos(u)*(1+sin(u))+max(-sign(u-pi),0)*4*(1- cos(u)/2)*cos(u)*cos(v)+max(sign(u-pi),0)*4*(1-cos(u)/2)*cos(v+pi) y = 16*sin(u)+max(-sign(u-pi),0)*4*(1-cos(u)/2)*sin(u)*cos(v) z = 4*(1-cos(u)/2)*sin(v)
x = -(2/15)*cos(u)*(3*cos(v)-30*sin(u)+90*cos(u)^4*sin(u)-
y = -(1/15)*sin(u)*(3*cos(v)-3*cos(u)^2*cos(v)- z = (2/15)*(3+5*cos(u)*sin(u))*sin(v) |
0 : 2 π
0 : π
|
0 : 2 π
0 : 2 π
|
|
|
Klein Bottle (Gray)
|
x = cos(u)(a+sin(v)cos(u/2)-sin(2v)sin(u/2)/2) y = sin(u)(a+sin(v)cos(u/2)-sin(2v)sin(u/2)/2) z = sin(u/2)sin(v)+cos(u/2)sin(2v)/2 |
a = 2 |
-π : π |
-π : π |
|
Klein Bottle (Nordstrand)
|
x = cos(u)(cos(u/2)(√2+cos(v))+sin(u/2)sin(v)cos(v)) y = sin(u)(cos(u/2)(√2+cos(v))+sin(u/2)sin(v)cos(v)) z = -sin(u/2)(√2+cos(v))+cos(u/2)sin(v)cos(v) |
-2 π : 2 π |
0 : 2 π |
|
|
Klein Cycloide
|
x = cos(u/int(c))*cos(u/int(b))*(int(a)+cos(v))+sin(u/int(b))*sin(v)*cos(v) y = sin(u/int(c))*cos(u/int(b))*(int(a)+cos(v))+sin(u/int(b))*sin(v)*cos(v) z = -sin(u/int(b))*(int(a)+cos(v))+cos(u/int(b))*sin(v)*cos(v) |
umax = 2 b c π |
0 : umax |
0 : 4 π |
|
Kuen Surface
|
x = (2*cosh(v)*(cos(u)+u*sin(u)))/(cosh(v)^2+u^2) y = (2*cosh(v)*(sin(u)-u*cos(u)))/(cosh(v)^2+u^2) z = v-(2*sinh(v)*cosh(v))/ (cosh(v)^2 + u^2) |
-5 : 5 |
-7 : 7 |
|
|
Kidney Surface
|
x = cos(u)*(3cos(v) - cos(3v)) y = sin(u)* (3cos(v) - cos(3v)) z = 3sin(v)-sin(3v) |
0 : 2 π |
-0.5π : 0.5 π |
|
|
Loops
|
x = (s*cos(u/t)+rr*cos(v))cos(u) y = (s*cos(u/t)+rr*cos(v))sin(u) z = s*sin(u/t)+rr*sin(v) |
|
0 : 20 π |
-π : π |
|
Pseudo Sphere
|
x = sech(t*u)cos(v) y = sech(t*u)sin(v) z =t*u-tanh(t*u)
sech(u)=1/cosh(t*u) |
t = 0 ... 1 für Animation |
-4 : 4 |
0 : 2 π |
|
3D Rose Curve
|
x = 0.5cos(u)(cos(n/d*u)+√(p^2+cos(n/d*u)^2)*sin(v*v_factor)) y = 0.5sin(u)(cos(n/d*u)+√(p^2+cos(n/d*u)^2)*sin(v*v_factor)) z = - z_factor*0.5(p+√(p^2+cos(n/d*u)^2)*cos(v*v_factor)) |
|
0 : 20 π |
-π : π |
|
Rotoide
|
x = f(u,v)*cos(v*t) - rr*cos(u)sin (v*t) y = f(u,v)*sin(v*t) + rr*cos (u)cos(v*t) z = (c+ rr*sin (u))cos(k*v*t)
f(u,v) = b + (c + rr*sin (u))*sin(k*v*t) |
t = 0 ... 1 für Animation |
0 : 2 π |
0 : 2 π |
|
Sievert Surface
|
x = rr(u,v)*cos(phi(u)) y = rr(u,v)*sin(phi(u)) z = (ln(tan(v/2))+a(u,v)(c+1)cos(v))/√c
phi(u)=-u/sqrt(c+1)+atan(tan(u)√(c+1)) a(u,v)=2/(c+1-c*sin(v)^2cos(u)^2) rr(u,v)=a(u,v)*√((c+1)(1+c*sin(u)^2))*sin(v)/√c |
c = 1 |
-0.5π : 0.5 π |
0.04 : 3.11 |
|
Steinbach- Schraube
|
x = u*cos(t*V) y = u*sin(t*v) z = v*cos(u) |
t = 0 ... 2 für Animation |
-3 : 3 |
0 : 2 π |
|
Stiletto
|
x = (2 + cos(u))*cos(v)^3 *sin(v) y = (2 + cos(u+2*pi/3))*cos(v+2*pi/3)^2*sin(v+2*pi/3)^2 z = -(2 + cos(u-2*pi/3))*cos(v+2*pi/3)^2*sin(v+2*pi/3)^2 |
0 : 2 π |
0 : 2 π |
|
|
Korkenzieher-Schraube
|
x = rr*(1 - abs(u)) sin(v) + RR (1 -abs(u)) sin(u*n*pi) y = rr*(1 - abs(u)) cos(v) + RR (1 - abs(u)) cos(u*n*pi) z = L*u
x = rr*(1 - abs(u)) sin(v) + RR (1 -abs(u)) sin(u*n*pi+c) y = rr*(1 - abs(u)) cos(v) + RR (1 - abs(u)) cos(u*n*pi+c) z = L*u
x = rr*(1 - abs(u)) sin(v) + RR (1 -abs(u)) sin(u*n*pi+2c) y = rr*(1 - abs(u)) cos(v) + RR (1 - abs(u)) cos(u*n*pi+2c) z = L*u |
|
-1 : 1 |
0 : 2 π |
|
Twisted Sphere
|
x = a*cos(u)cos(v) y = a*sin(v)+b* u-3*b z = a*sin(u)cos(v) |
0 : 2 π |
0 : 2 π |
|
|
Torus umwickelt (oszill. Rotoide)
|
Rototide:
f (x) = x+c*sin(x/a+t)-t*c x = (7+2*cos(f(u)))*cos(u/a/b) y = (7+2*cos(f(u)))*sin(u/a/b) z = 2*sin(f(u))
x = (7+0.7*cos(v))*cos(u) y = (7+0.7*cos(v))*sin(u) z = 0.7*sin(v) |
a = 12 b = 1 c = 7
t = 0 ... 2
π
|
0 : 24 π
0 : 2 π |
0 : 2 π
|
|
Torus umwickelt
|
x = (RT+rw*cos(p*u*t)+rt*cos(v))*cos(q*u*t) y = rt*sin(v)+rw*sin(p*u*t) z = (RT+rw*cos(p*u*t)+rt*cos(v))*sin(q*u*t)
x = (RT+rt*cos(v))sin(u) y = rt*sin(v) z = (RT+rt*cos(v))cos(u) |
t = 0 ... 1 für Animation
q ist Vielfaches von p |
0 : 2 π |
0 : 2 π |
|
Torus umwickelt (Linie)
|
 Linie:
x = (RT+(rw+a)*cos(p*u*t))*cos(q*u*t) y = (RT+(rw+a)*cos(p*u*t))*sin(q*u*t) z = (rw+a)*sin(p*u*t) |
wie Torus umwickelt
a : Abstand der Linie |
0 : 2 π |
0 : 2 π |
|
Torus-Knoten 1
|
wie Torus umwickelt |
wie Torus umwickelt
p und q teilerfremd |
0 : 2 π |
0 : 2 π |
|
Torus-Knoten 2
|
x = sin(n*u*t)*c(u,v) y = cos(n*u*t)*c(u,v) z = RR*0.5*(sin(5*u*t)+rr*sin(v))
c(u,v)=RR*(2+0.3*cos(5*u*t))+rr*cos(v) |
t = 0 ... 1 für Animation |
0
: 2 π |
0
: 2 π |
|
Umbilic Torus
|
x = sin(u) (7 + cos(u/3 - 2 v) + 2 cos(u/3 + v)) y = cos(u) (7 + cos(u/3 - 2 v) + 2 cos(u/3 + v)) z = sin(u/3 - 2 v) + 2 sin(u/3 + v)+3 |
0
: 2 π |
0
: 2 π |
|
|
Borromean Rings
|
 :x = (rb+rs*cos(v))*cos(u) y = (rb+rs*cos(v))*sin(u)+rb*√(3)/3 z = rs*sin(v)+3*sin(3*u+1+√(3)/3)
x = (rb+rs*cos(v))*cos(u)+0.5*rb y = (rb+rs*cos(v))*sin(u)-rb*√(3)/6 z = rs*sin(v)+3*sin(3*u+1+√(3)/3)
x = (rb+rs*cos(v))*cos(u)-0.5*rb y = (rb+rs*cos(v))*sin(u)-rb*√(3)/6 z = rs*sin(v)+3*sin(3*u+1+√(3)/3) |
rb = 10 rs = 2
mit rs = 2.5 berühren sich die Ringe |
0 : 2 π |
0 : 2 π |
|
Trianguloid Trifoil
|
x = 2 sin(3 u) / (2 + cos(v)) y = 2(sin(u) + 2 sin(2u)) / (2 + cos(v + 2 pi / 3)) z = (cos(u) - 2 cos(2 u)) (2 + cos(v)) (2 + cos(v + 2 pi / 3)) / 4 |
-π : π |
-π : π |
|
|
Wellenkugel
|
x = t*u*cos(cos(t*u))cos(v) y = t*u*cos(cos(t*u))sin(v) z = t*u*sin(cos(t*u)) |
t = 0 ... 1 für Animation |
0
: 5 π |
0 : 4.5 |
:
:
:
Torus:
Wicklung (wrapping):
Torus:
:
Quellen
Weitere Parameterflächen und mathematische Details dazu finden Sie z.B. unter
Eine wahre Fundgrube für parametrische Flächen ist die folgende Seite, der ich auch einige Beispiele entnommen habe und dort weitere Anregungen bekommen habe. Tatsächlich hat mich diese Seite damals motiviert, ein Programm zu suchen, mit denen man die Flächen plastischer darstellen kann als "nur" mit einem Drahtgittermodell, wenngleich diese auch ihren Reiz haben und ganz hervorragend auf der Seite präsentiert werden...