Länge eines Funktionsgraphen
Die Bogenlänge s im Intervall [a, b] eines Graphen einer stetig differenzierbaren Funktion y = f (x) errechnet sich zu
wobei f ' (x) die Ableitung (Steigungsfunktion) von f ist
[1].
Für einige geometrische Figuren und Funktionen lässt sich das Integral in geschlossener Form lösen, für eine Vielzahl von Funktionen existiert jedoch keine Stammfunktion bzw. deren Herleitung ist extrem aufwendig, so dass man auf die Numerische Integration zurückgreift.
Ist die Funktion in parametrischer Darstellung gegeben: x = fx (t), y = fy (t) (s.u. Länge einer Kardioide,
Länge des Graphen der parametrischen Funktion für einen Rotationskörper), so ergibt sich die Länge des Funktionsgraphen für t in den Grenzen ta und tb gemäß
Für eine Funktion in Polarkoordinaten ergibt sich die Länge des Graphens (s.u. Länge einer Archimedischen Spirale) zwischen den Winkeln φ0 und φ1 zu [2]:
Im folgenden finden Sie einige Beispiele für die Berechnung der Länge eines Funktionsgraphens.
Länge einer Parabel
In einem Quadrat mit der Seitenlänge 1 ist die Länge des Bogens (gelb in Grafik) der Parabel mit f (x) = x² in diesem Bereich gesucht.
Offensichtlich ist dieser Bogen länger als die Diagonale (blau in Grafik) mit dem Wert
Die Ableitung ist f ' (x) = 2 x. Somit ergibt sich für den Bogen s:
Das Integral kann in geschlossener Form gelöst werden:
Mit Graphing Calculator 3D und numerischer Integration erhält man mit n= 1000 für den Bogen
s = 1.4789428575445978. Der absolute Fehler ist kleiner als 10-13.
Länge einer Kettenlinie
Für eine Kettenline f (s. auch Kettenlinie) gilt:
Somit ergibt sich die Länge L der Kettenlinie im Intervall [a, b] zu
Für zwei Kettenlininen k1 und k2 wurden die Längen
Lk1 und Lk2 zwischen den Aufhängepunkten -1 und 1 berechnet. Zum Vergleich wurden auch die Längen Lp1 und Lp2 zweier approximierter Parabeln p1 und p2 berechnet:
Lk1 = 2.084381 Lk2 = 3.62685
Lp1 = 2.0836 Lp2 = 3.56757
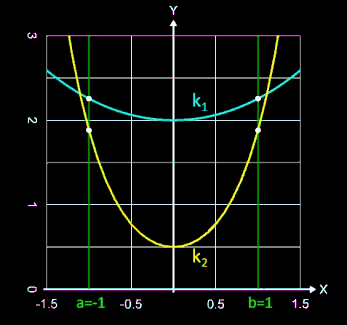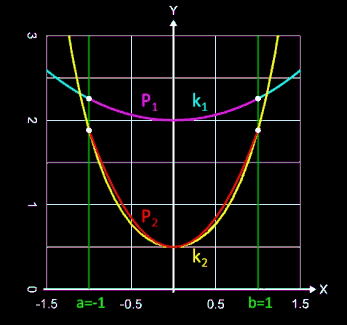
Kettenlinien:
k1 (x) = 2 cosh (x / 2)
k2 (x) = 0.5 cosh (x / 0.5)
Approximierte Parabeln:
p1 (x) = 0.255 x² + 2
p2 (x) = 1.381 x² + 0.5
Kreisumfang
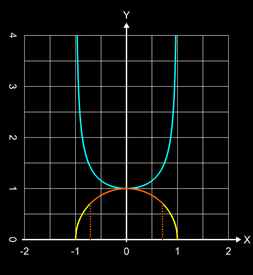
Der Umfang eines Kreises mit dem Radius 1 soll ermittelt werden.
Ein entsprechender Halbkreis im Intervall [-1, 1] lässt sich durch die Funktion
darstellen. Für die Ableitung ergibt sich
und somit für den Umfang s des Vollkreises:
Bei einer Lösung mit numerischer Integration ist zu beachten, dass der Integrand für x = -1 und x = 1 nicht definiert ist und s (x) (s. oben, blauer Graph) dort eine Polstelle besitzt.
Abhilfe schafft die numerische Integration für einen Viertelkreis (s. oben, orangener Graph) im Intervall
.
Die absolute Abweichung vom exakten Wert 0.5 π ist mit n = 1000 kleiner als 10-12.
Länge einer Sinusschwingung
Gesucht ist die Länge einer halben Sinuswelle für f (x) = sin (x) z.B. im Intervall (0, π).
Für das Integral
existiert keine geschlossene Stammfunktion. Mittels numerischer Integration ergibt sich die Lösung 3.820197789027712 mit einem absoluten Fehler kleiner als 10-13 bereits mit n = 20.
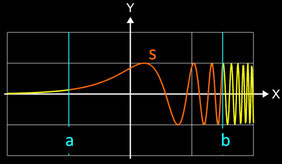
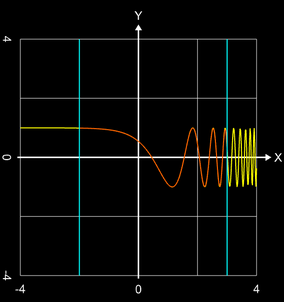
Länge von sin ( exp (x) )
Zu ermitteln ist die Länge des Funktionsgraphen von f (x) = sin
(ex) im Intervall [-2, 3] (s. blaue Markierungen in Grafik). Mit der Ableitung
f ' (x) = cos (ex) ex ergibt sich für den Bogen
Da keine Stammfunktion existiert, wird das Integral numerisch berechnet.
Mit z.B. n = 5000 ist der absolute Fehler kleiner als 10-13.
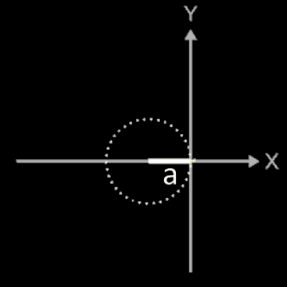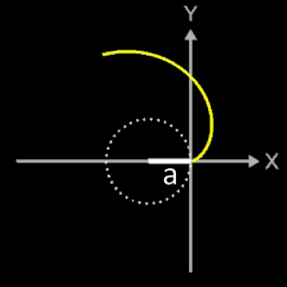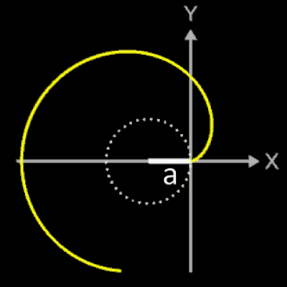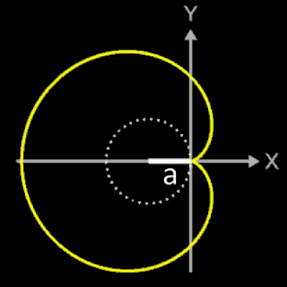
Länge einer Kardioide
Zu bestimmen ist die Länge einer Kardioide (s. Grafik). Sie wird erzeugt mit der parametrischen Funktion
x = fx (t) = a [ 1 - cos (t) ] cos (t)
y = fy (t) = a [ 1 - sin (t) ] cos (t)
in den Grenzen t = 0, ..., 2π.
fx ' (t) = a [ -sin (t) + 2 cos (t) sin (t) ]
fy ' (t) = a [ cos (t) - cos ² (t) + sin ² (t) ]
und somit
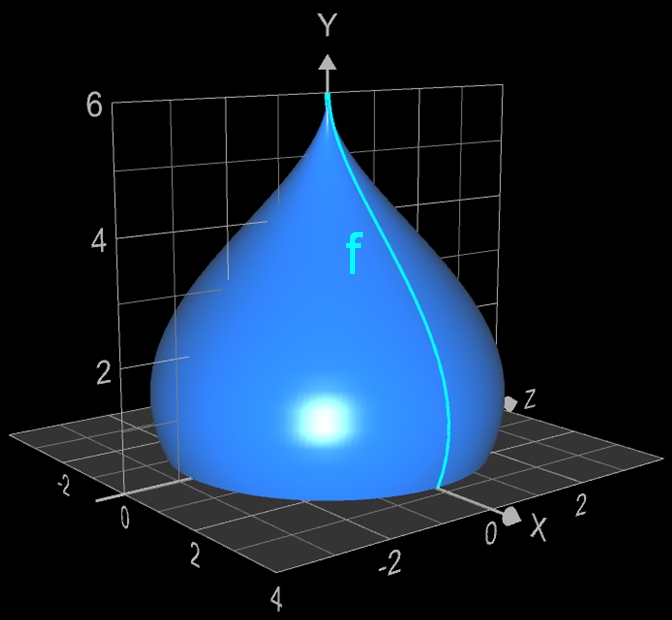
Länge des Graphen der parametrischen Funktion für einen Rotationskörper
Lässt man für t = asin (-0.2) ... π/2 die parametrische Funktion
x = fx (t) = 3 cos4 (t)
y = fy (t) = 5 sin (t) + 1
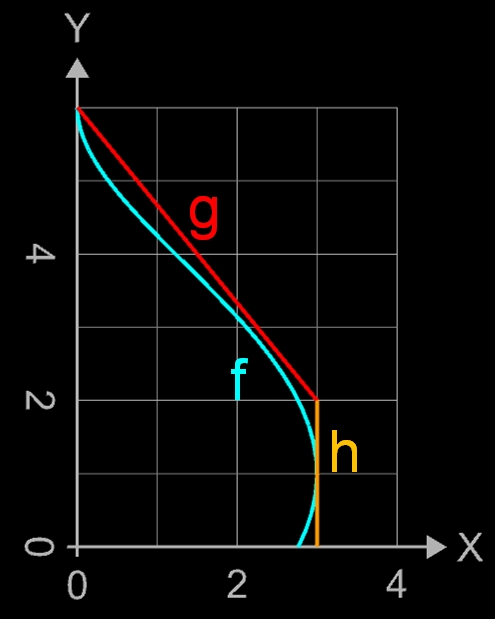
um die y-Achse eines Koordinatensystems rotieren, so entsteht die typische Kuppel eines Zwiebelturms (s. auch unter [3] für die Volumenbestimmung sowie unter [4] für die Bestimmung der Mantelfläche). Die Länge L des Funktionsgraphen im angegebenen Intervall soll bestimmt werden.
Zunächst soll die Länge abgeschätzt werden. Dazu betrachte man die Funktion g (x) = -4/3 x + 6 mit x = 0 ... 3 sowie die senkrechte Gerade h bei x = 3 in der Grafik.
Die geschätzte Länge La beträgt: La = √(3² + 4²) + 2 = 7.
Mit den Ableitungen
fx' (t) = -12 cos³ (t) sin (t) [ fx' (t) ]² = 144 cos6 (t) sin² (t)
fy' (t) = 5 cos (t) [ fy' (t) ]² = 25 cos² (t)
ergibt sich die Länge zu
Da keine Stammfunktion existiert, muss das Integral numerisch gelöst werden, z.B. mit dem Graphing Calculator 3D:
Wie man sieht, war die Längenabschätzung für f recht genau...
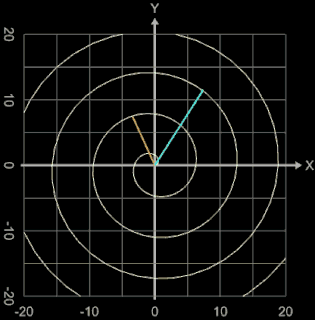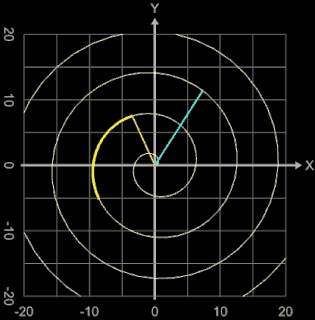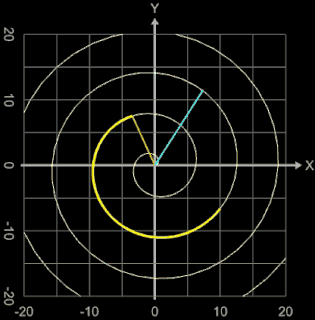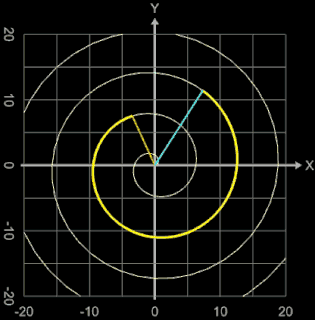
Länge einer Archimedischen Spirale in Polarkoordinaten
Die Archimedische Spirale wird erzeugt durch die Funktion f (φ) = a φ (s. auch Beispiel unter Fläche unter Funktion in Polarkoordinaten).
Mit der Ableitung f ' (φ) = a ergibt sich für die Länge L zwischen φ0 und φ1 mit φ0 ≥ 0, φ1 > φ0 :
In der animierten Grafik betragen a = 0,
φ0
= 2π
+ 2 und
φ1
= 4π
+ 1.
Die Differenz zwischen der Berechnung mit hergeleiteter Stammfunktion und der numerischen Berechnung mit dem Graphing Calculator 3D (s. Datei im Download-Bereich) ist kleiner als 10-13 :
Quellenverweise
[1] Sharma, A. K. (2005), Application Of Integral Calculus, Discovery Publishing House, S.101
[2] Singh, R. R. (2010), Engineering Mathematics, Tata McGraw-Hill, S. 6.17
[3] https://www.frassek.org/3d-mathe/rotationsk%C3%B6rper/volumen-mit-parametrischer-funktion/
[4] https://www.frassek.org/3d-mathe/rotationsk%C3%B6rper/mantelfl%C3%A4che/
Download