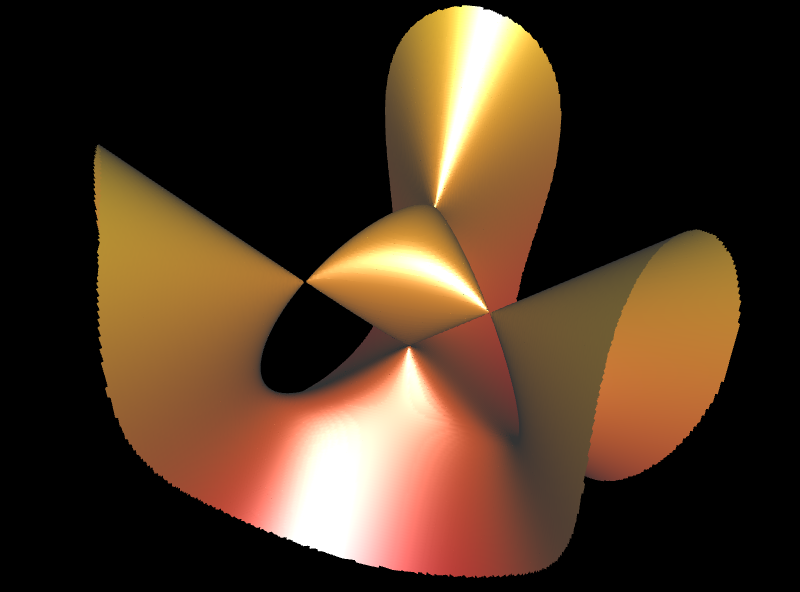Algebraische Flächen mit Singularitäten
Bei den Flächen auf dieser Seite handelt es sich ausschließlich um algebraische Flächen. Dies sind Flächen in impliziter
Darstellung, d.h. f (x, y, z) = 0 wobei
f (x, y, z) jedoch ein Polynom ist:
f = a1 m1 + a2 m2 + … + ar mr mit r ∊ {1, 2, 3, ...} und a1, a2, …, ar ∊ ℝ \ {0}
Hierbei ist mi ein Monom, d.h. es enthält nur Kombinationen aus Potenzen der Variablen x, y, z, wobei die Exponenten größer oder gleich 0 sind:
mi = xj yk zl mit j, k, l ∊ {0, 1, 2, 3, ...}
Unter dem Grad (engl. degree) eines Monoms m versteht man die Summe seiner Exponenten:
deg (m) = j + k + l,
der Grad d des Polynoms ist das Maximum der Grade der Monome:
d = deg (f) = max ( { deg (mi) }i=1,..,r )
Beispiele:
-
x² + y² + z² + 2
x y z – 1
d = 3, da deg (x y z) = 1 + 1 + 1 = 3
die Fläche mit f (x,y,z) = 0 nennt man Cubic
-
(x² + y² + z²)²
+ 8 x y z - 10 (x² +y² +
z²) + 25
d = 4, da die Auflösung der ersten Klammer ergibt: x4 + y4 + z4 + 2 x²y² + 2x²z² + 2y²z²
die Fläche mit f (x,y,z) = 0 nennt man Quadric
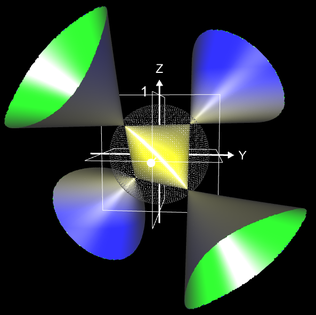
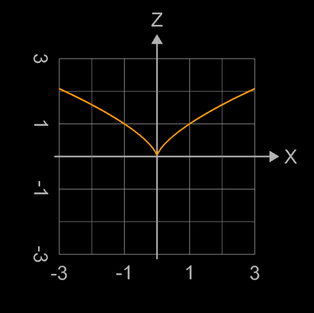
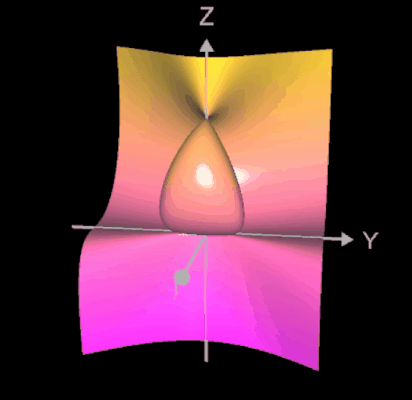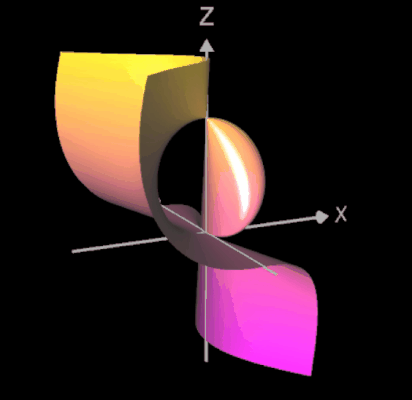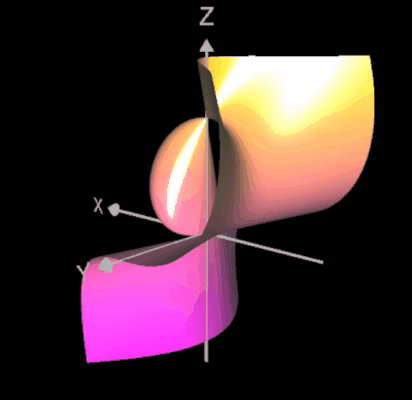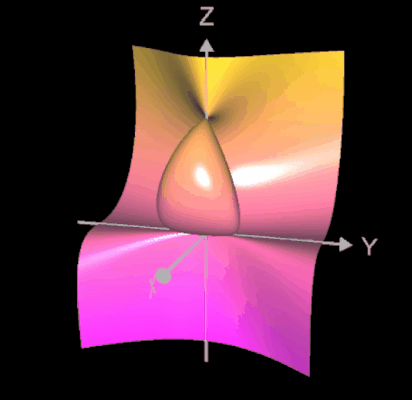
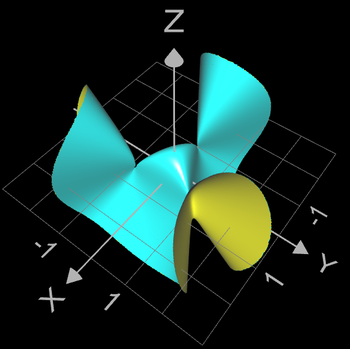
Algebraische Flächen können "glatt" sein, wie z.B. Kugel, Zylinder und Torus (vgl. Implizite Flächen). Es existieren jedoch auch solche Flächen, bei denen sich Teile der Fläche in einer "Spitze" berühren, wie z.B. beim Kegel mit der Gleichung f (x, y, z) = x² + y² - z² = 0 im Punkt (0 | 0 |0):
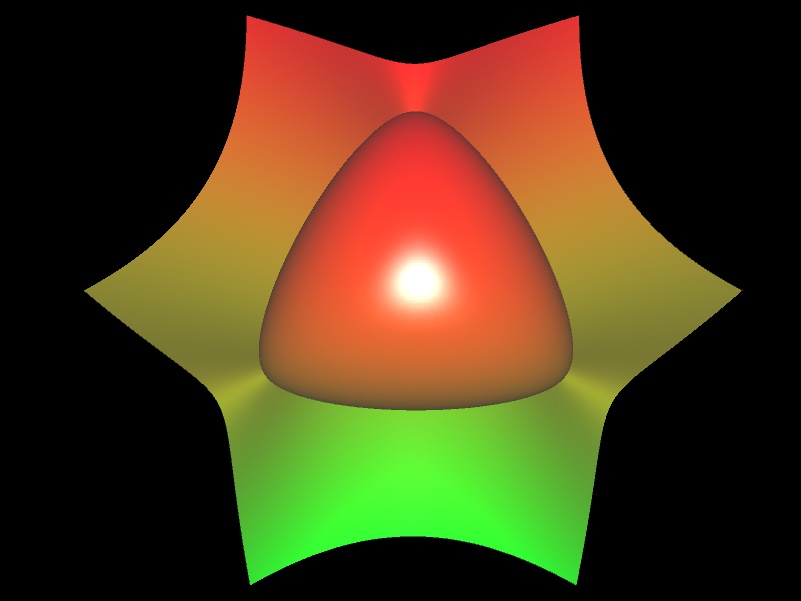
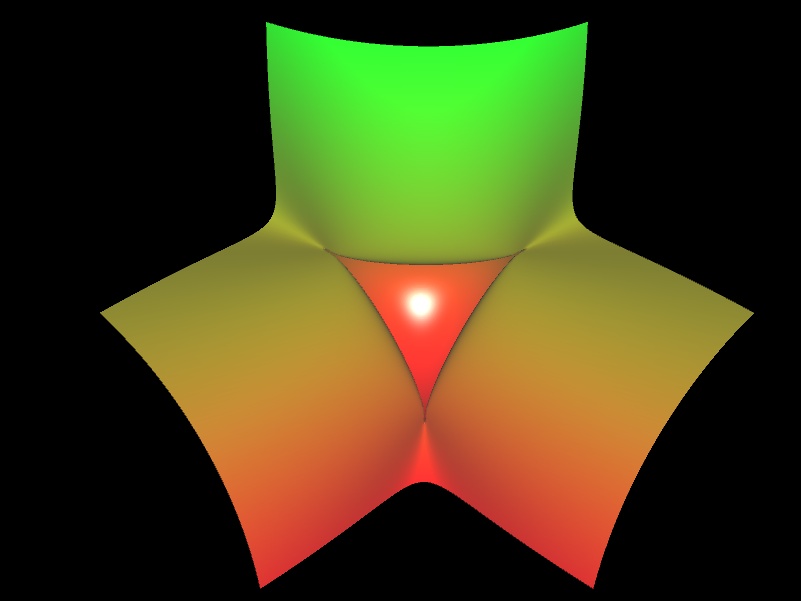
oder es existieren mehrere solcher Spitzen, wie z.B. bei den folgenden beiden Flächen.
Derartige Spitzen nennt man
Singularitäten. Singularitäten können sehr unterschiedlich aussehen (insbesondere nicht unbedingt spitz, s. auch ganz unten) und tauchen in vielen anderen
Gebieten der Mathematik, Physik, Technik und Natur auf.
Ein Punkt P (px | py | pz) einer
algebraischen Fläche mit der Gleichung f (x, y, z) = 0 heißt Singularität, falls sowohl
als auch alle partiellen Ableitungen von f gleich Null sind:
Andernfalls heißt P glatt (engl. smooth).
Während für jeden glatten Punkt einer algebraischen Fläche f eine Tangentialebene in diesem Punkt existiert, da der Gradient für f in diesem Punkt ungleich (0, 0, 0) ist, ist dies bei einer Singularität im Punkt P nicht der Fall, da ja für den Gradient im Punkt P gilt:
Flächen mit A1-Singularitäten ("nodes")
Die Singularitäten der obigen Beispiele sind die einfachsten Singularitäten und heißen gewöhnliche Doppelpunkte (engl. nodes) bzw. A1-Singularität. Eine solcher gewöhnlicher Doppelpunkt P hat unter allen Singularitäten die besondere Eigenschaft, dass die Determinate der Hessematrix H im Punkt P nicht verschwindet (also ungleich 0 ist):
Für die obige Quadrik ergibt sich z.B. für den Punkt (0 | √5 | 0) folgender Nachweis:
daraus folgt: Singularität im Punkt (0 | √5 | 0)
daraus folgt: (0 | √5 | 0) ist ein gewöhnlicher Doppelpunkt.
Eine Frage in der Grundlagenforschung auf dem Gebiet der algebraischen Geometrie ist die, wie viele Singularitäten eine algebraische Fläche vom Grad d maximal besitzen kann; diese Größe wird als µ(d) bezeichnet.
Für eine Ebene (d = 1) ist µ(d) = 0, für den Kegel (d = 2) ist µ(d) = 1. Für d = 3 ... 6 konnte µ(d) eindeutig bestimmt und entsprechende Flächen konstruiert werden:
| Grad | Fläche | µ (d) |
| 3 |
Caley Cubic • 1863 - Ludwig Schläfli: Beweis, dass µ (3) = 4 |
4 |
| 4 |
Kummer Quartic • 1875 - Eduard Kummer: Beweis, dass µ (4) = 16 |
16 |
| 5 |
Togliatti Quintic
• 1937 - E. Giuseppe Togliatti: Beweis der
Existenz der Quintic • 1980 - Arnaud Beauville: Beweis, dass µ (5) = 31 • 1990 - Konstruktion durch Wolf Barth |
31 |
| 6 |
Barth Sextic • 1996 - Konstruktion durch Wolf Barth • 1997 - Beweis, dass µ (6) = 65 |
65 |
Für d ≥ 7 wurden keine eindeutigen Werte für µ (d) gefunden, es wurden aber untere und obere Schranken für µ(d) nachgewiesen. Für die in den letzten drei Dekaden konstruierten Flächen in folgender Tabelle ist µ (d) gleich der unteren Schranke, die obere Schranke wurde nicht erreicht, und es ist auch noch nicht bekannt, ob sie je erreicht wird.
Die Konstruktion einer Fläche vom Grad d ≥ 7 mit der bislang größten Anzahl an Singularitäten stellt quasi einen Weltrekord dar; solch eine Fläche wird daher auch als "Weltrekordfläche" bezeichnet.
| Zeit | Grad d | µ (d) ≥ | Fläche | µ (d) ≤ |
| 2004 | 7 | 99 |
Labs Septic (Oliver Labs) |
104 |
| 1995 | 8 | 168 |
Endrass Octic (Stefan Endraß) |
174 |
| 2014 | 9 | 216 |
Escudero Nonic (Juan Escudero) (220 nodes) |
246 |
| 1996 | 10 | 345 | Barth Decic (Wolf Barth) | 360 |
| 1992 | 11 | 425 |
Chmutov Surface |
480 |
| 2006 | 12 | 600 |
Sarti Dodecic (Allessandra Sarti) |
645 |
In der obigen Tabelle ist µ (d) die maximal mögliche Anzahl komplexer Singularitäten einer algebraischen Fläche, wobei das zugrunde liegende Polynom auch komplexe Koeffizienten ai (vgl. ganz oben auf der Seite) haben darf. Es stellte sich aber heraus, dass in keinem der in der Tabelle aufgeführten Fälle eine bessere obere oder untere Schranke für eine reelle Variante µℝ (d) bekannt ist, so dass dort nicht weiter zwischen µℝ (d) und µ (d) unterschieden wird. Insbesondere haben alle Flächen, die die in der Tabelle angegebenen unteren Schranken realisieren, ausschließlich reelle Singularitäten, so dass diese visualisiert werden können (s. folgende Galerie).
Flächen mit A1-Singularitäten - Galerie
Die Gleichungen, Parameterwerte sowie weitere Informationen / Besonderheiten zu den folgenden Flächen finden Sie in der Tabelle am Ende der Seite.
Bei den meisten Flächen gibt es mehrere Ansichten. Verwenden
Sie die Steuerelemente oder klicken Sie auf die
Miniaturansicht, um sich gezielt ein Bild anzuschauen. Insbesondere lohnt sich eine vergrößerte, detailreichere Ansicht durch Klicken auf das Symbol .
Goursat Quartic I (12 nodes)
Goursat Quartic II (12 nodes)
Goursat Quartic III (12 nodes)
Goursat Quartic IV a (12 nodes)
Goursat Quartic IV b (12 nodes)
Goursat Quartic V (12 nodes)
Goursat Quartic VI (12 nodes)
Goursat Quartic VII a (12 nodes)
Goursat Quartic VII b (12 nodes)
Flächen mit A2-Singularitäten ("cusps")
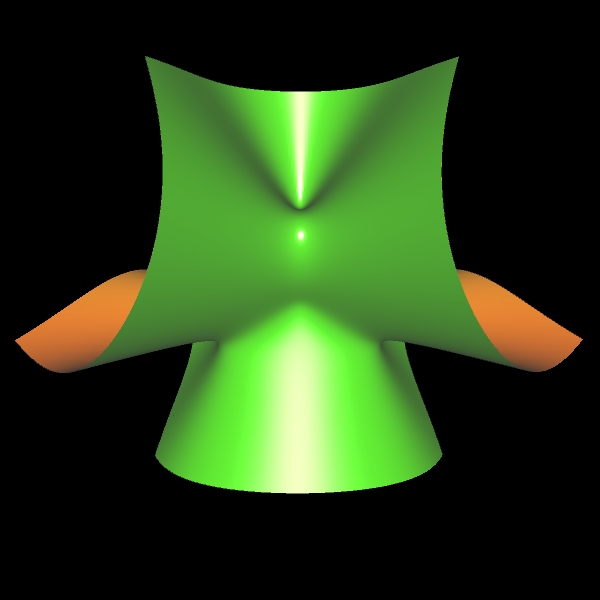
Ein weiterer Typ einer Singularität ist die sog. A2-Sigularität (engl. cusp, was soviel wie "Höcker" bedeutet). Im folgenden linken Bild ist eine solche Singularität im Punkt (0 | 0 | 0) für das definierende Polynom -x² + y² + z³ = 0 zu sehen.
Legt man durch die Fläche einen Schnitt mit y = 0, so ergibt sich die orangene algebraische Kurve zu
x² - y³ = 0 im rechten Bild mit einer Singularität in (0 | 0).
Wie auch bei den A1-Singularitäten gilt hier (vgl. oben):
jedoch ist im Gegensatz zu diesen bei A2-Singularitäten die Determinante der Hesse-Matrix im Punkt der Singularität gleich 0:
Die folgende Cubic mit dem definierenden Polynom f (x, y, z) = -x³ - y² z - x z² + x z = 0 besitzt sowohl eine A1-Singularität (Doppelpunkt) als auch eine A2-Singularität (cusp).
Die Singularitäten liegen in P (0 | 0 | 0) und Q (0 | 0 | 1) und es gilt:
f (P) = f (Q) = 0
det 𝓗f (P) = 0 det 𝓗f (Q) = 2
Somit liegt in P (0 | 0 | 0) eine A2-Singularität und in Q (0 | 0 | 1) eine A1-Singularität vor.
Eine Abwandlung der Caley Cubic (s.o.) zeigt das folgende Beispiel mit dem definierenden Polynom
und drei Cusps an den Stellen (-1 | 0 | 0), (½ | 1 | 0) und (-½ | 1 | 0).
So ergibt sich z.B. für den Punkt (-1 | 0 | 0) folgender Nachweis einer A2-Singularität:
daraus folgt: (-1 | 0 | 0) ist eine A2-Singularität (cusp).
Die folgende Cubic mit dem definierenden Polynom
x y z = k (x + y + z - a)³
besitzt 3 Cusps und wurde bereits im Jahr 1869 vom deutschen Mathematiker Olaus Henrici (1840 - 1919) untersucht.
Für die Beispielfläche wurde k = 0.1 und a = 5 gewählt.
Die folgenden beiden Flächen stellen auch "Weltrekorde" dar. Oliver Labs konstruierte in 2005 eine Quintic mit 15 cusps (es ist nachgewiesen, dass eine Quintic maximal 20 cusps haben kann), Wolf Barth konstruierte eine Sextic mit 30 reellen cusps (36 komplexe cusps).
Die folgende Tabelle stammt aus der Publikation A Sextic with 35 Cusps von Oliver Labs aus 2005. Sie zeigt die bekannten Einschränkungen für die Anzahl µA2 der A2-Singularitäten (cusps) in Abhängigkeit vom Grad des definierenden Polynoms.
| Grad | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | d |
| µA2 ≤ | 0 | 3 | 8 | 20 | 37 | 62 | 98 | 144 | 202 | 275 | ¼ d (d-1)² |
| µA2 ≥ | 0 | 3 | 8 | 15 | 35 | 52 | 70 | 126 | 159 | 225 | ≈ 2/9 d³ |
Algebraische Flächen mit Singularitäten - Tabelle der Funktionen und Parameter
| Fläche | Funktion | x | y | z |
| Caley Cubic |
x^3+y^3+z^3+1-0.25*(x+y+z+1)^3 = 0 mit x^2+y^2+z^2 <= 4^2 Die 4 Singularitäten (1 | -1 | 1), (1 | 1 | -1), (-1 | 1 | 1), (-1 | -1 | -1) bilden Eckpunkte eines Tetraeders, die 6 reellen Geraden sind die verlängerten Kanten des Tetraeders. |
-4 : 4
|
-4 : 4
|
-4 : 4
|
|
Version Hunt:
(x+y+z-a) (x*y+y*z+z*x) - 2*x*y*z = 0 a = 0.4
Von den 9 reellen Geraden liegen 6 (weiß) auf den Kanten desTetraeders,
(x = -a/2, y = -u, z = u), (x = -u, y = -a/2, z = u), (x = -u, y = u, z = -a/2).
|
-1 : 1 |
-1
: 1 |
-1 : 1 |
|
|
Version Endraß:
(x+y+z+1)*(-x-y+z+1)*(x-y-z+1) + (x+y+z+1)*(-x-y+z+1)*(-x+y-z+1)
Die 6 reellen Geraden (weiß) liegen auf den Kanten desTetraeders, der durch die 4 Singularitäten |
-2.5
: 2.5 |
-2.5
: 2.5 |
-2.5
: 2.5 |
|
|
Labs
|
x^3+3x^2-3x*y^2+3y^2-4+z^3+3z^2 = 0
x^2+y^2+z^2 <= 6^2 |
-6
: 6 |
-6
: 6 |
-6
: 6 |
|
Sauermann Cubic
|
x^3+3*x^2*(-1+y)-3*y^2-3*x* y^2-y^3+(1+z)*(1+2*z-4*z^2)^2=0
x^2+y^2+z^2-15.625<=0 |
-4
: 4 |
-4
: 4 |
-4
: 4 |
|
Cubic
|
(x^2)+z*x^2+y^2*z-2*z^3+3*z^2-z=0
x^2+y^2+z^2<=9
|
-3
: 3 |
-3
: 3 |
-3
: 3 |
|
Nordstrand
|
25(x^3(y+z)+y^3(x+z)+z^3(x+y))+50(x^2y^2+x^2z^2+y^2z^2)-125(x^2*y*z+y^2*x*z+z^2*x*y)
x^2+y^2+z^2 <= 2^2 |
-2
: 2 |
-2
: 2 |
-2
: 2 |
|
Goursat Quartic
|
erzeugende Gleichung: x^4+y^4+z^4 + k1*(x^2+y^2+z^2)^2 + k2*a^2*(x^2+y^2+z^2) + k3*a^4 = 0 |
|||
|
Typ I (12 nodes):
k1 = 0 k2 = -2 k3 = 2 a = 2 12 Singularitäten (± a, ± a, 0) in den Scheitelpunkten des Kuboktaeders max ( 2|x|, 2|y|, 2|z|, |x+y+z|, |-x+y+z|, |x-y+z|, |x+y-z| ) = a² |
-2
: 2 |
-2
: 2 |
-2
: 2 |
|
|
Typ II (12 nodes):
k1 = 0 k2 = 2 k3 = -2 a = 2 12 reelle Geraden auf den Kanten des Oktaeders |x| + |y| + |z| = a |
-3.5
: 3.5 |
-3.5
: 3.5 |
-3.5
: 3.5 |
|
|
Typ III (12 nodes):
k1 = -1/2 k2 = 1 k3 = -3/2 a = 2 12 reelle Geraden auf den Diagonalen des Würfels max ( |x|, |y|, |z| ) = a |
-4
: 4 |
-4
: 4 |
-4
: 4 |
|
|
Typ IV a (12 nodes):
k1 = -1 k2 = 4 k3 = -6 a = 2 12 reelle Geraden als verlängerte Kanten des Würfels max ( |x|, |y|, |z| ) = a
Typ IV b (12 nodes):
k1 = -1 k2 = 4 k3 = -6 a = 2 gleiche Fläche wie Typ IV a |
-3
: 3
-6 : 6 |
-3
: 3
-6 : 6 |
-3
: 3
-6 : 6 |
|
|
Typ V (12 nodes):
k1 = -1/3 k2 = -2/3 k3 = 2/3 a = -2 12 Singularitäten (± a, ± a, 0) in den Scheitelpunkten des Kuboktaeders max ( 2|x|, 2|y|, 2|z|, |x+y+z|, |-x+y+z|, |x-y+z|, |x+y-z| ) = a² |
-3.5 : 3.5 |
-3.5 : 3.5 |
-3.5 : 3.5 |
|
|
Typ VI (12 nodes):
k1 = -1 k2 = 2 k3 = -2 a = 2 12 Singularitäten (± a, ± a, 0) in den Scheitelpunkten des Kuboktaeders max ( 2|x|, 2|y|, 2|z|, |x+y+z|, |-x+y+z|, |x-y+z|, |x+y-z| ) = a² 12 reelle Geraden als verlängerte Diagonalen der Quadrate des Kuboktaeders
|
-3.5 : 3.5 |
-3.5
: 3.5 |
-3.5
: 3.5 |
|
|
erzeugende Gleichung: (x+y+z-s) (-x-y+z-s) (x-y-z-s) (-x+y-z-s) - t*(x^2+y^2+z^2-3*s)^2 = 0 |
||||
|
Typ VII a (12 nodes):
s = 1 t = 1 4 Dreifach-Singularitäten auf den Ecken (1 | 1 | -1), (-1 | 1 | 1), (1 | -1 | 1), (-1 | -1 | -1) des Tetraeders
max(abs(-x+y+z-1),max(abs(x-y+z-1),max(abs(x+y-z-1),abs(-x-y-z-1))))-2=0 |
-3
: 3 |
-3
: 3 |
-3
: 3 |
|
|
Typ VII b (12 nodes):
s = 2 t = 1 12 Singularitäten in den Seitenmitten von 4 der 8 Dreiecksflächen des Kuboktaeders
|
||||
|
Typ VIII a (12 nodes):
s = 1 t = 2 4 Dreifach-Singularitäten auf den Ecken (1 | 1 | -1), (-1 | 1 | 1), (1 | -1 | 1), (-1 | -1 | -1) des Tetraeders
max(abs(-x+y+z-1),max(abs(x-y+z-1),max(abs(x+y-z-1),abs(-x-y-z-1))))-2=0
|
||||
|
Typ VIII b (12 nodes):
s = 2 t = 2 12 Singularitäten in den Seitenmitten von 4 der 8 Dreiecksflächen des Kuboktaeders
|
||||
|
Kummer
|
a=0.5 s=√2 (x^2+y^2+z^2-2.25)^2-5.75/0.75*(1-z-s*x)*(1-z+s*x)*(1+z+s*y)*(1+z-s*y) = 0
x^2+y^2+z^2<=4 |
-4
: 4 |
-4
: 4 |
-4
: 4 |
|
Togliatti
|
w=1 64*(x*w)*(x^4-4*w*x^3-10*x^2*y^2-4*x^2*w^2+16*w^3*x-20*w*x*y^2+5*y^4 +16*w^4-20*y^2*w^2)-5*√(5-√5)*(2*z-√(5-√5)*w)*(4*(x^2+y^2-z^2)+(1+3*√5)*w^2)^2 = 0
x^2+y^2+z^2 <= 8^2 |
-8
: 8 |
-8
: 8 |
-8
: 8 |
|
Version Barth:
a=-(8/5)*(1+1/(√5))*sqrt(5-√5) b= (1/4)*(1+3*√5) c=(1/2)*sqrt(5-√5)
a*(x-z)*(cos((2*pi)/5)*x-sin((2*pi)/5)*y-z)*(cos((4*pi)/5)*x-sin((4*pi)/5)*y-z)*(cos((6*pi)/5)*x-sin((6*pi)/5)*y-z)*(cos((8*pi)/5)*x-sin((8*pi)/5)*y-z)+(1-c*z)*(x^2+y^2-1+b*z^2)^2 = 0
x^2+y^2+z^2 <= 4^2 |
-8
: 8 |
-8
: 8 |
-8
: 8 |
|
|
Goursat Sextic |
erzeugende Gleichung: z^6-5*(x^2+y^2)*z^4+5*(x^2+y^2)^2*z^2-2(x^4-10x^2*y^2+5*y^4)*x*z +k1*(x^2+y^2+z^2)^3+k2*a^2*(x^2+y^2+z^2)^2+k3*a^4*(x^2+y^2+z^2)+k4*a^6 = 0
x^2+y^2+z^2 <= 3^2 |
|||
|
Typ I (30 nodes):
k1 = 0 k2 = 1 k3 = -2 k4 = 1 a = 1
Oberfläche mit 30 Singularitäten an den Ecken eines Ikosidodekaeders. |
-3
: 3 |
-3
: 3 |
-3
: 3 |
|
|
Typ II (30 nodes):
k1 = 0 k2 = -1 k3 = 2 k4 = -1 a = 1
Oberfläche mit 30 Singularitäten an den Ecken eines Ikosidodekaeders.
Sie besteht aus 20 Grundschichten, den dreieckigen Flächen des Ikosidodekaeders. |
||||
|
Barth
|
p= (1+√5)/2 q=p^2
4*(q*x^2-y^2)*(q*y^2-z^2)*(q*z^2-x^2)-(1+2*p)*(x^2+y^2+z^2-1)^2 = 0 |
-2
: 2 |
-2
: 2 |
-2
: 2 |
|
Sarti
|
w=1
x^6+y^6+z^6+w^6+15(x^2*y^2*z^2+x^2*y^2*w^2)+15(x^2*z^2*w^2+y^2*z^2*w^2) -
x^2+y^2+z^2<=16
Variante 2: x^6+y^6+z^6+w^6+15(x^2*y^2*z^2+x^2*y^2*w^2) +15(x^2*z^2*w^2+y^2*z^2*w^2)-2/3(x^2+y^2+z^2+w^2)^3 = 0 |
-4
: 4 |
-4
: 4 |
-4
: 4 |
|
Septic
|
x^5-10*x^3*y^2-5*(x^2+y^2)^2+20*(x^2+y^2)+5*x*y^4+8*(0.5*z^7-3.5*z^5+7*z^3-3.5*z-1)-16 = 0 |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Labs
|
b= - 0.140106854987124776454220549858
x^7-21*x^5*y^2+35*x^3*y^4-7*x*y^6+7*x^6+21*x^4*y^2+21*x^2*y^4+7*y^6-57*x^4-114*x^2*y^2- -100)*x^2*y^2*z^3+(-49*b^2+7*b-50)*y^4*z^3+(5776/7*b^2-5648/49*b+5888/7)*x^2*z^3 +(5776/7*b^2-5648/49*b+5888/7)*y^2*z^3+(-313136/343*b^2+6288/49*b-319264/343)*z^3 +(3680/7*b^2-3608/49*b+536)*x^2*z^4+(3680/7*b^2-3608/49*b+536)*y^2*z^4+(-592240/343*b^2 +11856/49*b-603856/343)*z^4+(816/7*b^2-800/49*b+832/7)*x^2*z^5+(816/7*b^2-800/49*b +832/7)*y^2*z^5+(-458832/343*b^2+1312/7*b-467840/343)*z^5+(-166272/343*b^2+3328/49*b -169536/343)*z^6+(-166272/2401*b^2+3328/343*b-169536/2401)*z^7 = 0
x^2+y^2+z^2<=64 |
-8
: 8 |
-8
: 8 |
-8
: 8 |
|
Heider
|
(x*0.8358-(z-0.5)*0.549)*(x*cos(2*pi/7)*0.8358-y*sin(2*pi/7)*0.8358-(z-0.5)*0.549) *(x*cos(4*pi/7)*0.8358-y*sin(4*pi/7)*0.8358-(z-0.5)*0.549)*(x*cos(6*pi/7)*0.8358 -y*sin(6*pi/7)*0.8358-(z-0.5)*0.549)*(x*cos(8*pi/7)*0.8358-y*sin(8*pi/7)*0.8358 -(z-0.5)*0.549)*(x*cos(10*pi/7)*0.8358-y*sin(10*pi/7)*0.8358-(z-0.5)*0.549) *(x*cos(12*pi/7)*0.8358-y*sin(12*pi/7)*0.8358-(z-0.5)*0.549)-(x^2+y^2-4.731)^2 = 0
x^2+y^2+z^2<=49 |
-7
: 7 |
-7
: 7 |
-7
: 7 |
|
van
|
0.99*(64*(0.5*z)^7-112*(0.5*z)^5+56*(0.5*z)^3-7*(0.5*z)-1)+(0.7818314825-0.3765101982*y- 0.7818314825*x)*(0.7818314824-0.8460107361*y-0.1930964297*x)*(0.7818314825-0.6784479340*y +0.5410441731*x)*(0.7818314825+0.8677674789*x)*(0.7818314824+0.6784479339*y +0.541044172*x)*(0.7818314824+0.8460107358*y-0.193096429*x)*(0.7818314821+0.3765101990*y -0.781831483*x) = 0
x^2+y^2+z^2<=36 |
-6
: 6 |
-6
: 6 |
-6
: 6 |
|
Breske
|
(2*x^7-42*x^5*y^2+70*x^3*y^4-14*x*y^6-14*x^6+70*x^4*y^2+70*x^2*y^4-14*y^6+28*x^5+56*x^3*y^2
+28*x*y^4-84*x^2*y^2+28*y^4-42*x^3-42*x*y^2+14*x^2-14*y^2+14*x)+0.5*(64*z^7-
x^2+y^2+z^2<=25 |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Chmutov
|
x^8+y^8+z^8-2*x^6-2*y^6-2*z^6+1.25*x^4+1.25*y^4+1.25*z^4-0.25*x^2-0.25*y^2 -0.25*z^2+0.03125 = 0 |
-1
: 1 |
-1
: 1 |
-1
: 1 |
|
Endraß
|
s=√2 (-1/4*(1-s)*(x^2+y^2)^2+(x^2+y^2)*((1-1/s)*z^2+1/8*(2-7*s))-z^4+(0.5+s)*z^2-1/16*(1-12*s))^2-(x-1)*(s/2*x+s/2*y-1)*(y-1)*(-s/2*x+s/2*y-1)*(-x-1)*(-s/2*x-s/2*y-1)*(-y-1)*(s/2*x-s/2*y-1) = 0
x^2+y^2+z^2<=25
Variante 2: s= - √2 |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Sarti Octic
|
3584*z^4+256*z^8+1792*z^4*x^4+10752*z^2*x^4+1792*x^4+256*x^8+256+1792*z^4*y^4 +10752*z^2*y^4+1792*y^4+256*y^8+10752*z^4*x^2*y^2-21504*z^2*x^2*y^2+10752*x^2*y^2 +3584*x^4*y^4+192(-1-12*x^4*y^2*z^2-24*x^2*y^2*z^2-12*x^2*y^2-12*x^2*z^2-12*y^2*z^2
-12*x^4*y^2-12*x^4*z^2-12*x^2*y^4-12*x^2*z^4-12*y^4*z^2-12*y^2*z^4-4*x^6*y^2
x^2+y^2+z^2<=25 |
-7
: 7 |
-7
: 7 |
-7
: 7 |
|
Sarti Octic
|
x^8+y^8+z^8+1+14(x^4*y^4+x^4*z^4+x^4+y^4*z^4+y^4+z^4)+168*x^2*y^2*z^2 -9/16*(x^2+y^2+z^2+1)^4 = 0 |
-7
: 7 |
-7
: 7 |
-7
: 7 |
|
Breske
|
x^9-36*x^7*y^2+126*x^5*y^4-84*x^3*y^6+9*x*y^8+64*z^9-9*x^8+126*x^6*y^2-126*x^2*y^6 +9*y^8+27*x^7- 27*x^5*y^2-135*x^3*y^4-81*x*y^6-144*z^7-21*x^6-225*x^4*y^2+45*x^2*y^4 -39*y^6-36*x^5+72*x^3*y^2+108*x*y^4+108*z^5+54*x^4+108*x^2*y^2+54*y^4+9*x^3 -27*x*y^2-30*z^3-27*x^2-27*y^2+2.25*z+4.25 = 0
x^2+y^2+z^2<=16 |
-4
: 4 |
-4
: 4 |
-4
: 4 |
|
Escudero
|
d=9 L(x,y,k) = y-(cos(k*2*pi/(6d))-x)*tan(k*pi/(6d))-sin(k*2*pi/(6d)) lambda(d) = 3^((1-(-1)^d)/4)*(-1)^(floor((d+3)/6)+1) J(x,y) lambda(d)*L(x,y,1)*L(x,y,7)*L(x,y,13)*L(x,y,19)*L(x,y,25)*L(x,y,31)*L(x,y,37)*L(x,y,43)*L(x,y,49) Q(x,y,z) = J(x,y)+(-1)^(d+1)/4*(J(z,0)-1+(-1)^(d+1)*2) = 0
x^2+y^2+z^2 <=25 |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Barth Decic |
p= (√5+1)/2
8(x^2-p^4*y^2)(y^2- p^4*z^2)*(z^2-p^4*x^2)*(x^4+y^4+z^4-2*x^2*y^2-2*x^2*z^2-2*y^2*z^2)+(3+5p)(x^2+y^2+z^2-a)^2*(x^2+y^2+z^2-(2-p))^2
x^2+y^2+z^2<=9 |
-3
: 3 |
-3
: 3 |
-3
: 3 |
|
Sarti
|
-22* (1+x^2+y^2+z^2)^6 +243*(48* (x^2*y^2+z^2) * (y^2+x^2*z^2) * (x^2+y^2*z^2) -352*x^2*y^2*z^2*(x^2+y^2+z^2 +x^2*y^2 +x^2*z^2 +y^2*z^2) +336*x^2*y^2*z^2* x^2*y^2 +x^2*z^2 +y^2*z^2) * (1+x^4+y^4+z^4)^2 -14*(1+x^4+y^4+z^4) * ((z^2+x^2*y^2) *
(y^2+x^2*z^2) +(z^2+x^2*y^2) * (x^2+y^2*z^2)+ (x^2+y^2*z^2) * (y^2+x^2*z^2)) -6* (1+x^4+y^4+z^4)*((z^2+x^2*y^2)^2 + (y^2+x^2*z^2)^2+(x^2+y^2*z^2)^2) +33*sqrt(5) *
((x^2*y^2+z^2)^2 * (y^2+x^2*z^2) - (y^2+x^2*z^2)^2 * (x^2*y^2+z^2) - (x^2*y^2+z^2)^2 * (x^2+y^2*z^2) + (y^2+x^2*z^2)^2 * (x^2+y^2*z^2) + (x^2+y^2*z^2)^2 * (x^2*y^2+z^2) -
(x^2+y^2*z^2)^2 * (y^2+x^2*z^2)) +
x^2+y^2+z^2<=25 |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Escudero
|
wie Escudero Nonic, aber mit
d=12
J(x,y)=lambda(d)*L(x,y,1)*L(x,y,7)*L(x,y,13)*L(x,y,19)*L(x,y,25)*L(x,y,31)*L(x,y,37)*L(x,y,43)*L(x,y,49) |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Escudero
(1162
|
wie Escudero Nonic, aber mit
d=15
J(x,y)=lambda(d)*L(x,y,1)*L(x,y,7)*L(x,y,13)*L(x,y,19)*L(x,y,25)*L(x,y,31)*L(x,y,37)*L(x,y,43)*L(x,y,49) |
-5
: 5 |
-5
: 5 |
-5
: 5 |
|
Henrici Surface (3 cusps)
|
k = 0.1 a = 5
x y z = k (x + y + z - a)³
3 neunfache reelle Geraden: (t, a-t, 0), (a-t, 0, t), (0, t, a-t) |
-8
: 8 |
-8
: 8 |
-8
: 8 |
|
Labs
|
x^5-10*x^3*y^2+5*x*y^4-3*z^5-5*x^4-10*x^2*y^2-5*y^4+10*z^3+20*x^2+20*y^2-15*z-24 = 0
x^2+y^2+z^2<=36 |
-6
: 6 |
-6
: 6 |
-6
: 6 |
|
Barth
|
a=1
4*((a*(1+sqrt(5))/2)^2*x^2-y^2)*((a*(1+sqrt(5))/2)^2*y^2-z^2)*((a*(1+sqrt(5))/2)^2*z^2-x^2)- |
-1.5 : 1.5 |
-1.5 : 1.5 |
-1.5 : 1.5 |
Quellen
- Oliver Labs, Hypersurfaces with Many Singularities, Dissertation (PDF)
- Alessandra Sarti, Pencils of Symmetry in P³, Dissertation (PDF)
- S. Breske, O. Labs, D. van Straten, Real Line Arrangements and Surfaces with many Real Nodes,
https://arxiv.org/pdf/math/0507234.pdf - S. Holzer, O. Labs (2006) Illustrating the classification of real cubic surfaces, Algebraic Geometry and Geometric Modeling (pp.119-134), DOI:10.1007/978-3-540-33275-6_8
- J.G. Escudero, A construction of algebraic surfaces with many real nodes,
https://arxiv.org/pdf/1107.3401.pdf - O. Labs, World Record Surfaces,
https://imaginary.org/sites/default/files/imaginary-worldrecordsurfaces-oliver-labs.pdf - https://imaginary.org/gallery/oliver-labs
- https://imaginary.org/program/surfer
-
O. Labs (2005) A Sextic with 35 Cusps,
https://www.researchgate.net/publication/2118063_A_Sextic_with_35_Cusps
-
Encyclopédie des formes mathématiques remarquables, https://mathcurve.com/