Modellierung eines 3D Würfels
Es mag vielleicht ein wenig verwundern, dass ein einfaches Objekt wie ein Würfel an dieser Stelle auftaucht. Jedoch gibt es mehrere Ansätze, um eine Funktion aufzustellen, die einen Würfel mit der Kantenlänge a erzeugt.
Für die folgenden Betrachtungen soll der geometrische Mittelpunkt des Würfels mit der Kantenlänge a in
(0 | 0 | 0) eines Koordinatensystems liegen.
Würfel in Parameterdarstellung

Ein Würfel mit der Kantenlänge a soll parametrisiert werden. Dazu betrachte man zunächst eine Kugel, die ihren geometrischen Mittelpunkt ebenfalls in (0 | 0 | 0) hat, vollständig im Würfel liegt und maximal groß ist. Somit beträgt ihr Durchmesser a bzw. ihr Radius ½ a (s. Bild rechts).
Sie lässt sich erzeugen mittels der parametrischen Funktion
x (u,v) = ½ a cos(u) sin(v)
y (u,v) = ½ a sin(u) sin(v)
z (u,v) = ½ a cos(v)
mit 0 ≤ u ≤ π und 0 ≤ v ≤ 2π.
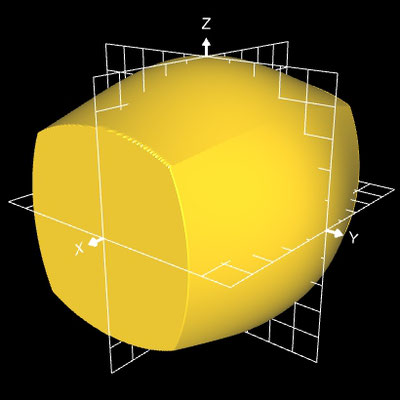
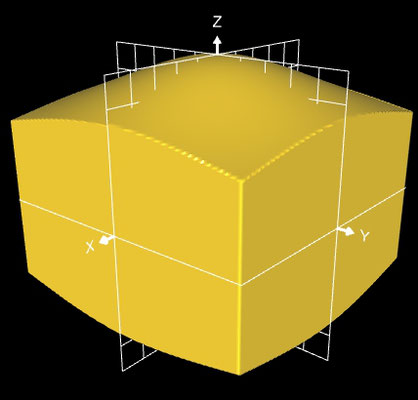
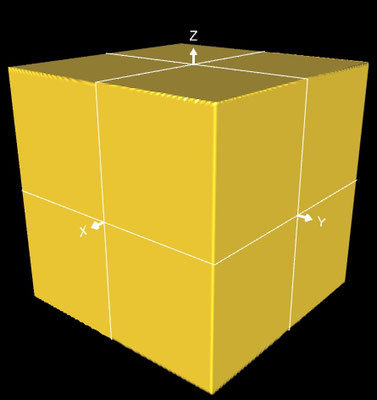
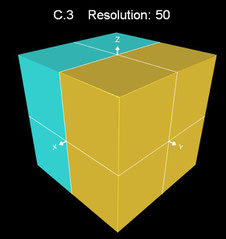
Nun kann man vom Kugelmittelpunkt aus die Kugeloberfläche auf die Würfeloberfläche projizieren. Mit
m (u, v) = max ( |cos(u) sin(u)|, |cos(u) sin(v)|, |cos(v)| )
ergibt sich dann mit 0 ≤ u ≤ π und 0 ≤ v ≤ 2π:
x (u,v,a) = ½ a cos(u) sin(v) / m(u,v)
y (u,v,a) = ½ a sin(u) sin(v) / m(u,v)
(C.1)
z (u,v,a) = ½ a cos(v) / m(u,v)
Die linke Grafik in der folgenden Galerie zeigt eine Projektion nur für die x-Achse, bei der mittleren Grafik erfolgte die Projektion nur für die x- und y-Achse; die dritte Grafik zeigt den fertigen Würfel.
Würfel als Super-Ellipsoid
Mit einem Super-Ellipsoid ergibt sich eine weitere parametrische Darstellung eines Würfels:
c (u,n) = sign(cos(u)) |cos(u)| n
s (v,n) = sign(sin(v)) |sin(u)| n
x (u,v,a) = ½ a c(v,n1) c(u,n1)
y (u,v,a) = ½ a c(v,n1) s(u,n1)
z (u,v,a) = ½ a s(v,n1)
mit -π
≤ u ≤
π und -π/2 ≤ v ≤
π/2. Hierbei ist n1 sehr klein zu wählen (z.B. 0.0001).
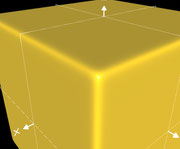
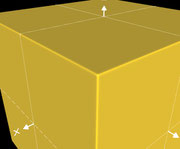
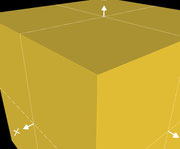
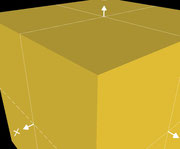
Die folgende Galerie zeigt für verschiedene Werte für n1
jeweils einen Ausschnitt einer Würfelecke.
Klicken Sie in der Galerie auf ein Bild für eine größere Ansicht, um die Qualität des erzeugten Würfels (Rundung der Kanten) besser vergleichen zu können,
Würfel in impliziter Darstellung
Eine implizite Darstellung der Würfelfunktion ergibt sich unmittelbar aus den geometrischen Eigenschaften der Würfeloberfläche:
max [ | x |, | y |, | z | ] = ½ a (C.2)
Eine weitere implizite Darstellung für die Würfeloberfläche ist:
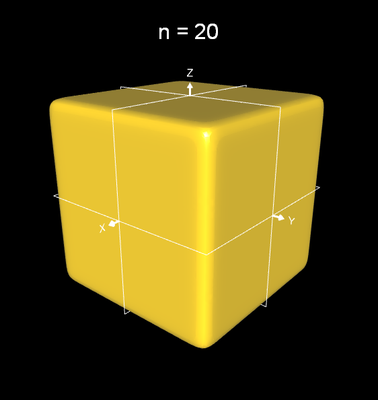
x n + y n +z n = (½ a) n (C.3)
Für n = 2 ergibt sich eine Kugel; mit größer werdenden Werten für n nähert sich der "Würfel" mit runden Kanten immer mehr der Idealform, so dass n hinreichend groß zu wählen ist:
Performance-Vergleich
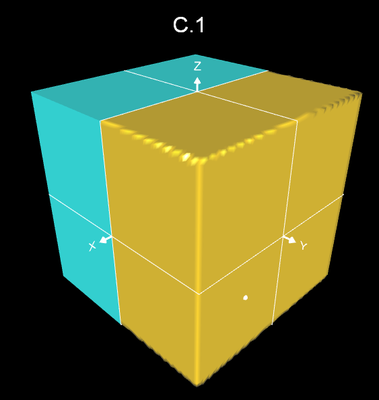
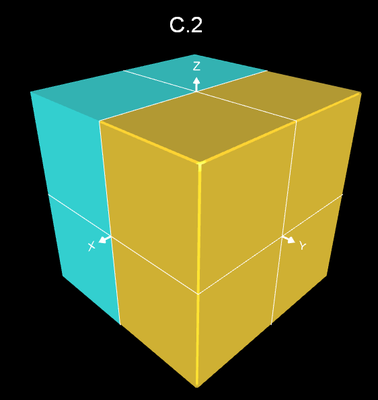
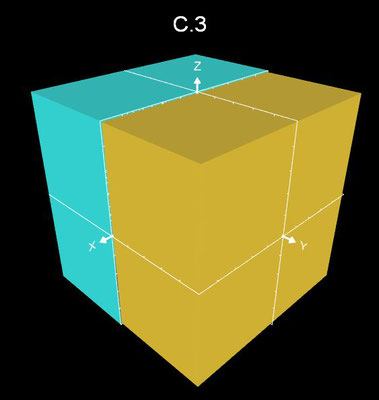
Die obigen Funktionen C.1 bis C.3 sowie das Super-Ellipsoid wurden mit Graphing Calculator 3D einem Vergleich im Hinblick auf die erzeugte Form unterzogen. Die Auflösung wurde für alle gleich gewählt (Resolution = 10). Die Rechenzeit lag dabei unter einer Sekunde.
Wie erwartet schneidet das Super-Ellipsoid am besten ab. In der nachstehenden Bildfolge ist dieses als halber Würfel in blau dargestellt.
Um die Qualität der mit verschiedenen Verfahren erzeugten Würfel besser vergleichen zu können, klicken Sie in der Galerie auf ein Bild für eine größere, detailreichere Ansicht.
Die Funktion C.1 schneidet am schlechtesten ab. Um ein Ergebnis wie im folgenden Bild dargestellt zu erhalten, muss die Auflösung auf 50 erhöht werden, die Rechenzeit liegt dann aber im Minutenbereich.
Mit der Funktion C.3 können zwar bei einer Auflösung von 10 recht scharfe Kanten erzeugt werden, allerdings ist der erzeugte Würfel etwas zu klein, da der Kantenwert 1 beim Lösen der impliziten Gleichung nicht erreicht wird (s. Bildfolge oben rechts, Bild vergrößern). Der Fehler beträgt 0.25 % der Kantenlänge a.
Bemerkenswert ist das Super-Ellipsoid mit den obigen Einstellungen: mit n1 = 0.0001 bei einer Auflösung von 1 und einer mit meiner Stoppuhr nicht messbar kurzen Rechenzeit beträgt der maximale Kantenfehler ca. 0.0004 % von a.