Oloid
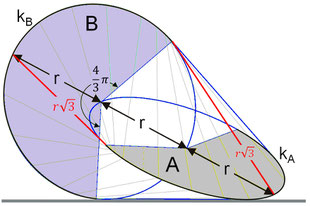
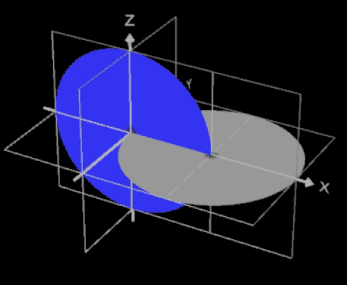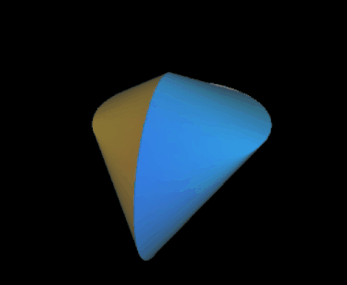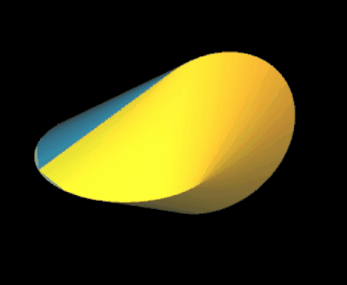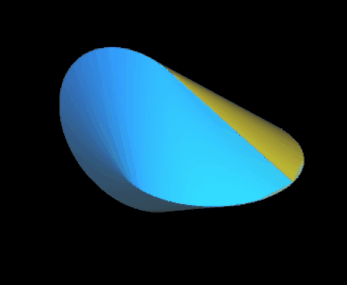
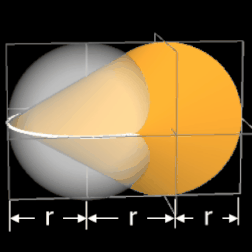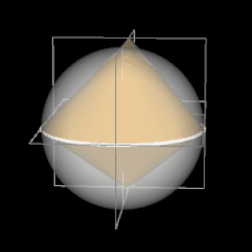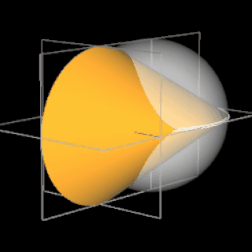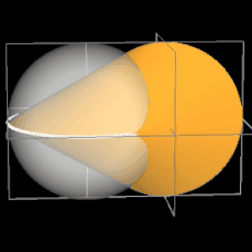
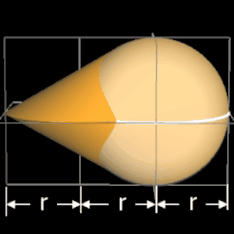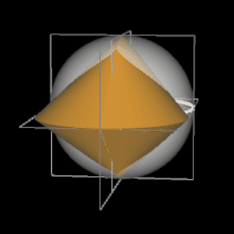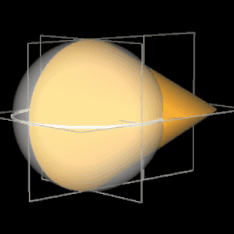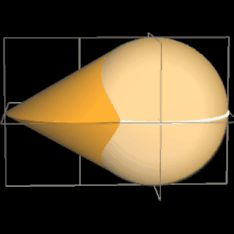
Das Oloid ist ein geometrischer Körper, der 1929 vom Bildhauer und Maschinenbauer Paul Schatz bei seinen Arbeiten zum umstülpbaren Würfel entdeckt wurde [1]. Analytisch untersucht wurde es 1997 von H. Dirnböck und H. Stachel [2]. Mathematisch gesehen ist es die konvexe Hülle zweier Kreise A und B mit gleichem Radius r, die sich senkrecht schneiden, wobei der Mittelpunkt eines Kreises genau auf der Peripherie des anderen Kreises liegt.
Das Oloid hat keine Ecken, jedoch zwei Kanten kA und kB , nämlich je einen 4π/3 = 240°-Bogen der beiden sich schneidenden Kreise, und ist ansonsten glatt. Den Torso des Oloids im kartesischen Koordinatensystem erhält man für
mit der Parametrisierung
Das Oloid ist, wie auch das Sphericon, einer der wenigen bekannten Körper, die über ihre gesamte Oberfläche abrollen. Die beim Abrollen entstehende Fläche ist somit gleichzeitig sein Netz. Um dieses zu konstruieren, betrachte man zunächst ¼ der Abrollkurve von kA. Diese ergibt sich zu (Gleichung 11 in [2a]):
mit t = 0, ..., 2π/3 und endet im Punkt (a | b) mit
Da die Abrollkurven von kA
und kB
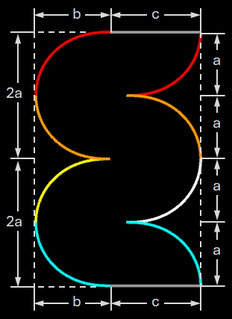
kongruent sind, lässt sich mit Hilfe der Symmetrieeigenschaften das Netz des Oloids konstruieren
(c = √3 r ≈
1.7321 r), s. Grafik rechts sowie bei
[2b].
Die folgende anschauliche Animation zum Abrollen der Oberfläche des Oloids auf einer Ebene habe ich bei [3] gefunden und leicht modifiziert.
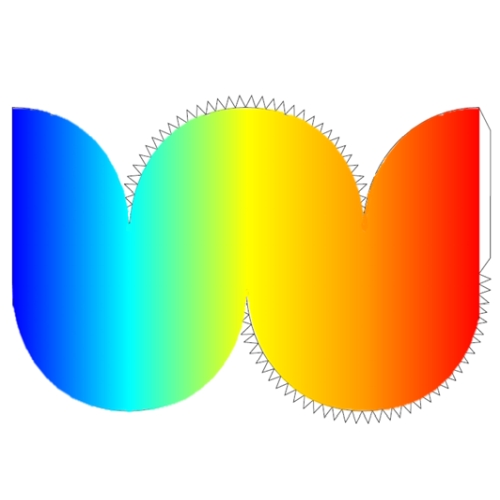
Ein buntes Netz des Oloids habe ich mit Graphing Calculator 3D berechnet, mit Klebefähnchen versehen (s. Download-Bereich am Seitenende), ausgedruckt, ausgeschnitten und zusammengeklebt (s. Fotostrecke; etwas verbeult, und man sieht, dass ich lange nicht mehr gebastelt habe ☺).
Setzt man das Oloid auf eine Schräge, so rollt es in einer taumelnden Bewegung (mäandernd) hinunter, ohne dabei jemals über seine Kanten zu poltern. Dieses Abrollen zeigen in der folgenden Galerie die linke und mittlere Animation [4a], [4b], das Video rechts zeigt das Abrollen eines realen Oloids aus Edelstahl.
Die Oberfläche des Oloids ergibt sich zu 4 π r² [2a]. Somit ist sie exakt so groß ist wie die einer Kugel mit gleichem Radius der beiden Kreise:
Das Volumen des Oloids ist eine irrationale Zahl, die nur auf numerischem Weg ermittelt werden und ca. 3.0524 r beträgt [2a].
Das Oloid kann als Teil einer algebraischen Fläche vom Grad 8 gesehen werden. Die Lösungsmenge der definierenden Polynomgleichung [5]
4 x2 + 4 x3 - 7 x4 - 8 x5 + 2 x6 + 4 x7 + x8 + 4 y2 + 4 x y2 - 18 x2
y2 - 16 x3 y2 + 14 x4 y2
+ 12 x5 y2 - 11 y4 - 8 x y4 + 22 x2 y4 + 12 x3 y4
- 6 x4 y4 + 10 y6 + 4 x y6 - 8 x2 y6 - 3 y8 + 4 x z2 - 6 x2 z2 - 48 x3
z2 - 46 x4 z2 - 12 x5 z2 - 10 y2 z2 - 52 x y2 z2 - 46 x2 y2 z2
+ 12 x3 y2 z2
+ 6 x4 y2 z2 + 24 x y4 z2 + 12 x2 y4 z2 + 6 y6 z2 + z4 - 8 x z4
- 50 x2 z4 - 36 x3 z4 - 6 x4 z4
- 12 y2 z4 + 12 x2 y2 z4 - 9 y4 z4 - 2 z6 - 20 x z6
- 8 x2 z6 + 6 y2 z6 - 3 z8 = 0
liefert die Oberfläche eines Oloids mit Radius r = 1, eingebettet in den |R³ mit dem Mittelpunkt der Fläche in (½ | 0 | 0) (s. Animation rechts).
Ich musste einfach ein reales Oloid mein eigen nennen und wurde fündig bei [6]. Ich habe mich für ein Oloid aus einem karelischen Birkenholz mit wunderschöner Maserung und einer Länge von ca. 100 mm entschieden - ein echtes Meisterwerk der Holzkunst (s. folgende Galerie). Zwar ist es ein Unikat, jedoch können interessierte Leser Oloide in diversen Größen, vielerlei Holzsorten und zu einem fairen Preis bei [6] erwerben.
Dort findet man auf einer Unterseite [7] auch eine originelle Idee zur Rollbewegung des Oloids. Im Video bahnt sich der kleine Kerl mäandernd seinen Weg durch den Schnee (Video in voller Länge/Größe bei [7]).
Download
Der Oloid "Bastelbogen" zum Ausschneiden enthält auf einer DIN A4 Seite das Netz des Oloids versehen mit Klebefähnchen.Tipps (bzw. Erkenntnisse nach dem eigenen Basteln): Papier besser etwas dicker als normales Schreibmaschinenpapier wählen, einen schnell härtenden, gelartigen Bastelkleber (z.B. UHU hart) verwenden.
Quellenverweise
[1] https://de.wikipedia.org/wiki/Oloid
[2b]
A. Kuleshov et al. (2011) On the Motion of the Oloid Toy, Proceedings of XXXIX International Summer
School–Conference APM 2011
[3] https://www.geogebra.org/m/qezw4fyh
[4a] http://www1.ttcn.ne.jp/~a-nishi/oloid/z_ani_1.html
[4b] http://www1.ttcn.ne.jp/~a-nishi/oloid/z_ani_2.html
[5] https://mathcurve.com/surfaces.gb/orthobicycle/orthobicycle.shtml