Sphericon
Das Sphericon wurde erstmals 1969 entdeckt, als der britische Zimmermann und mathematische Laie Colin Roberts nach einer Umsetzung des Möbiusbandes in Form eines geometrischen Körpers ohne Loch suchte [1]. Da ihm sein Objekt wie eine Kugel (engl. sphere) aus Kegeln (engl. cones) vorkam, nannte er es "Sphericon".
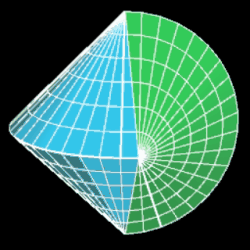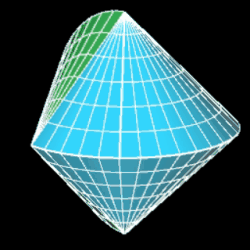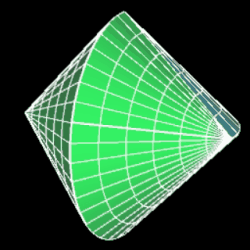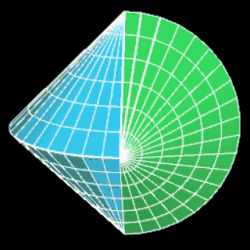
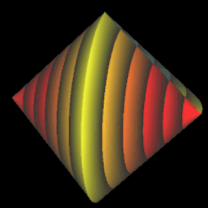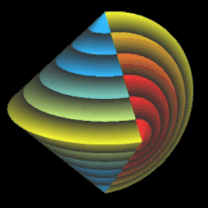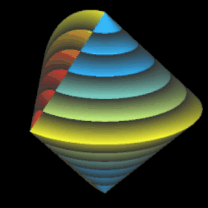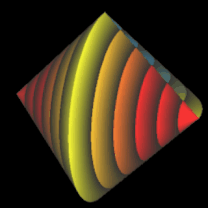
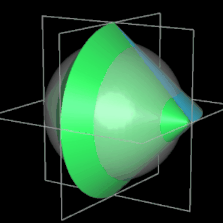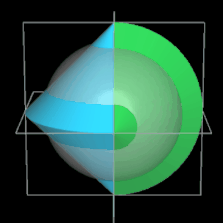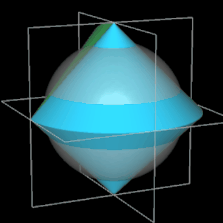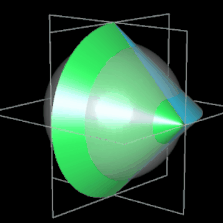
Es ist ein dreidimensionaler geometrischer Körper mit einer kontinuierlichen, abwickelbaren Oberfläche, zwei kongruenten, halbkreisförmigen Kanten und vier Eckpunkten, die ein Quadrat aufspannen. Er entsteht aus einem Doppelkegel, indem dieser entlang einer Ebene durch beide Spitzen geteilt wird, eine der beiden Hälften um 90° gedreht und die beiden Hälften wieder zusammengefügt werden. Damit die Schnittflächen beider Hälften identisch sind, müssen Radius r und Höhe h der Kegel gleich sein.
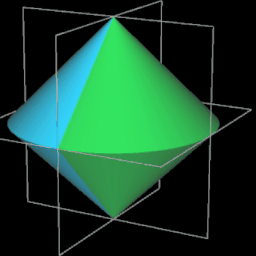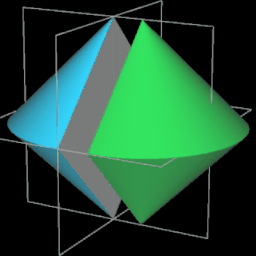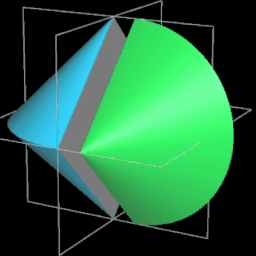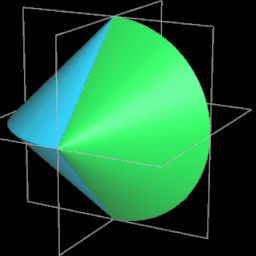
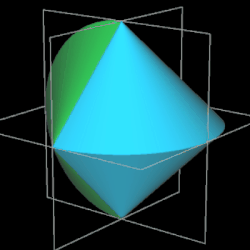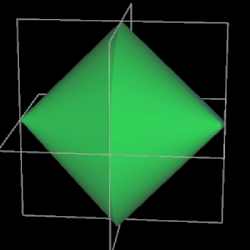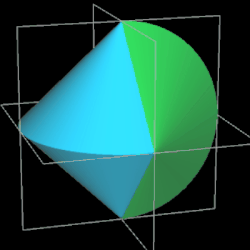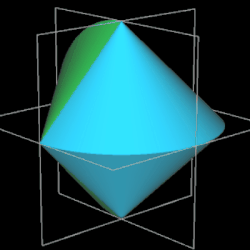
Während der Ausgangskörper vor dem Halbieren zwei Flächen und eine Kante besitzt, hat das Sphericon genau eine Fläche und zwei Kanten. Ich habe im Folgenden die usprüngliche Farbe der beiden Hälften beibehalten, was aber nicht bedeutet, dass es beim Sphericon zwei unterschiedliche Flächen gibt.
Stößt man das Sphericon an, so rollt es ähnlich dem Oloid
seine gesamte Oberfläche auf dem Untergrund ab. Da die Netze von Kegeln Kreissektoren sind und ein Sphericon aus vier Halbkegeln besteht, ist das Sphericon-Netz eine Kette aus vier kongruenten
Kreissektoren mit alternierender Orientierung (s. folgende Grafik links). Beim Abrollen entsteht somit eine torkelnde, jedoch tendenziell
geradlinige Bewegung.
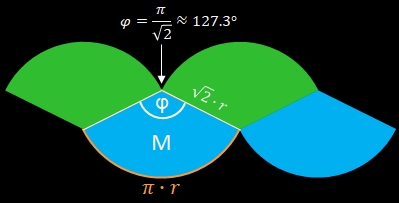
Die Radien der vier Kreissektoren sind die Berührstrecken des Sphericons (und somit zugleich die Schenkel des Kegelmantels) mit der Länge √2 r.

Die Sektorbögen haben jeweils eine Länge des halben Umfangs des Sphericons, also π r. Für den Winkel φ gilt der proportionale Zusammenhang
Die Oberfläche des Sphericons ist identisch mit der Mantelfläche MS und beträgt das Doppelte der Mantelfläche MK des Kreiskegels mit Radius r und gleicher Höhe h:
Sein Volumen VS ist das Doppelte des Kegelvolumens VK:
und entspricht somit dem Volumen einer Halbkugel mit dem Radius r des Sphericons bzw. einer Kugel mit dem Radius 0.51/3 r (s. beide folgenden Animationen). Das Foto rechts zeigt ein aus Kirschholz hergestelltes Sphericon mit einem Radius von ca. 3.8 cm [3].
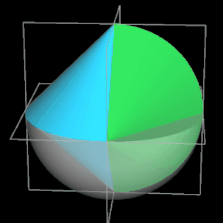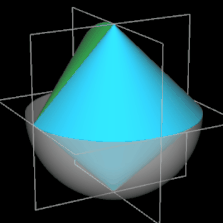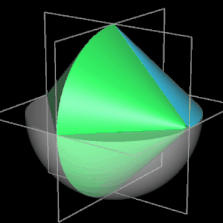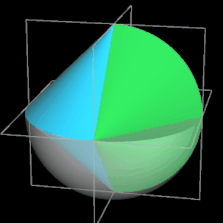
Sphericon aus Kirschholz [3]
Abschließend noch eine Spielerei mit unterschiedlichen Einfärbungen...