3D Spielwürfel
... eine kleine Spielerei, die mit dem Graphing Calculator 3D erzeugt wurde ...
Der 3D Spielwürfel mit der Kantenlänge 2•R wurde mit der impliziten Funktion
x20 + y20 + z20 - R20 = 0
erzeugt und hat seinen Mittelpunkt in (0 | 0 | 0) (s. auch Spezielle Flächen / 3D Würfel).

Da sich ein Würfelauge als weiß ausgefüllte Kreisfläche nur mit einer parametrischen Funktion erzeugen lässt, der Editieraufwand für die 21 Augen mir aber zunächst zu hoch erschien, habe ich zu einer kleinen "Schummelei" gegriffen; die Punkte auf dem sich drehenden Würfel oben auf der Seite sind in Wirklichkeit kleine Kugeln mit dem Radius r und dem Mittelpunkt ( xc | yc | zc), die nur ein wenig aus der Würfeloberfläche ragen (s. rechte Grafik). Dazu wurde die Funktion
f (x, y, z, xc, yc, zc) = (x - xc)² + (y - yc)² + (z - zc)² - r²
definiert und entsprechend der Augenzahl und -anordnung auf der jeweiligen Würfelfläche in impliziter Darstellung f (x, y, z, ,...) = 0 aufgerufen (insgesamt 21 Aufrufe).
Nun gut ... so hoch ist der Editieraufwand nun auch wieder nicht. Bei den folgenden 3D Spielwürfeln wurden die flachen Würfelaugen mit 21 parametrischen Funktionen erzeugt.
Ein Würfelauge (engl. pips) ist eine Kreisscheibe. Für ein Würfelauge in der xy-Ebene mit dem Radius rad und den Mittelpunktskoordinaten xc und yc lautet die parametrische Funktion folglich
mit u, v = 0, ..., 1 und der halben Kantenlänge R.
Durch Erhöhen der Exponenten von 20 auf 120 in der den Würfelkorpus bildenden Funktion hat der folgende halbtranparente Spielwürfel scharfe Kanten und gleicht dem abgebildeten Casino-Würfel [1], der in der Regel sogar nummeriert ist.
Die folgende Grafik zeigt 24 isometrische Ansichten dieses Würfels.

Noch etwas aufwendiger wird die Modellierung eines Spielwürfels mit Graphing Calculator 3D, will man die Würfelaugen als farbige Vertiefungen realisieren, wie dies bei sehr vielen Spielwürfeln der Fall ist (s. Grafik rechts).
Hierzu wird jede Fläche des Würfels in 9 gleichgroße Teilquadrate aufgeteilt.
Dort, wo bei einer Würfelfläche die Augen plaziert werden sollen, wird mit einer parametrischen Funktion ein Quadrat mit einem Loch erzeugt, z.B. für ein Teilquadrat in der xy-Ebene (s. folgende Grafik) mittels
mit u, v = 0, ..., 1 und der halben Kantenlänge R.

In das Loch wird dann eine Halbkugel mit dem Lochradius rad (ebenfalls eine parametrische Funktion) eingebettet.
Der Würfel besteht somit aus 6•9 + 21 = 75 parametrischen Funktionen.
Durch Zusammenfassen leerer quadratischer Teilflächen, die kein Auge enthalten, zu einer größeren Fläche (s. Grafik unten) lässt sich die Anzahl reduzieren auf
(2•1 + 4) + (2•2 + 4) + (2•3 + 4) + (2•4 + 3) + (2•5 + 4) + (2•6 + 1) = 62 parametrische Funktionen.
Abgerundete Kanten und Ecken lassen sich mit der zuvor beschriebenen Methode leider nicht ohne weiteres realisieren, diese müssten hinzugefügt werden: 12 Kanten in Form von Zylindern, 8 Ecken in Form von Kugeln. Einen solchen "Rahmen", bestehend aus Zylindern (orange) und Kugeln (rot) zeigt das linke Bild in der folgenden Galerie. In diesen wird der Würfel eingebettet (mittleres Bild), was dann mit farblicher Anpassung den fertigen Würfel ergibt (rechtes Bild).
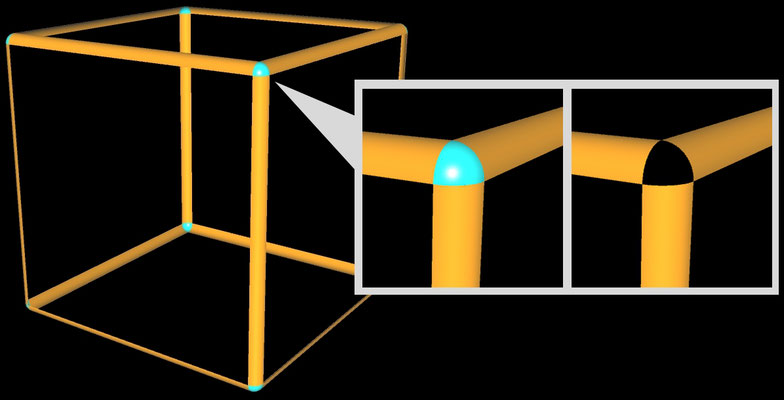
Praktischerweise reicht es aus, eine Kante als Viertelzylinder und eine Ecke als Achtelkugel zu realisieren (s. folgendes Bild). So werden nur noch 748 257 statt 905 565 Punkte bei gleicher Auflösung berechnet und somit die Rechenzeit reduziert.
Bei den folgenden zwei Würfeln wurden die Kanten noch weiter verrundet...


Um abgerundete Kanten und Ecken sowie Vertiefungen zu realisieren, kann man auch folgendermaßen vorgehen:
- Wie zu Anfang der Seite basiert der Würfelkörper auf der impliziten Funktion
W (x,y,z,xc,yc,zc) = x20 + y20 + z20 - R20.
-
Ein Auge (Pip) ist eine Kugel gemäß
P (x, y, z, xc, yc, zc) = (x - xc)² + (y - yc)² + (z - zc)² - r².
-
In einer einzigen impliziten Funktion wird das Produkt aus der Würfelfunktion und den Augenfunktionen gebildet; es entsteht
der abgebildete Würfel (s. auch unter Implizite Flächen mit einer Darstellung dieser und
ähnlicher Modellierungsmethoden).
Hier zum besseren Verständnis das Programm für den Graphing Calculator:
Die Rechenzeit für eine halbwegs brauchbare Auflösung ist sehr hoch: für die 175 000 Bildpunkte benötigte das Programm trotz meiner schnellen Hardware (s. Tools) 292 Sekunden. Außerdem haben bei dieser Methode die Augenvertiefungen die gleiche Farbe wie der Würfelkörper.
Mit einem Trick lassen sich die Würfelaugen dennoch - wohl mehr oder weniger gut - einfärben, indem ein Würfel mit etwas kleinerer Kantenlänge und anderer Farbe (z.B. weiß oder schwarz) im Inneren des gelben Würfels erzeugt wird: