Türme von Hanoi
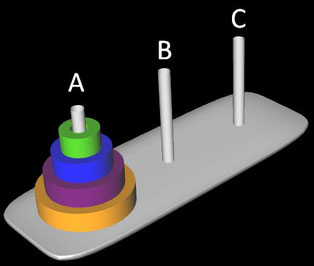
Die Türme von Hanoi sind ein altes mathematisches Knobel- und Geduldsspiel [1].
Das Spiel besteht aus drei gleich großen Stäben A, B und C, auf die mehrere verschieden große, gelochte Scheiben gelegt werden. Zu Beginn liegen alle Scheiben auf Stab A, der Größe nach geordnet, mit der größten Scheibe unten und der kleinsten oben.
Ziel des Spiels ist es, mit möglichst wenig Zügen den kompletten Scheiben-Stapel von A nach C zu versetzen.
Bei jedem Zug darf nur eine Scheibe eines beliebigen Stabes auf einen der beiden anderen Stäbe gelegt werden; dabei darf niemals eine größere auf eine kleinere Scheibe gelegt werden. Folglich sind zu jedem Zeitpunkt des Spieles die Scheiben auf jedem Stab der Größe nach geordnet.
Man kann zeigen, dass bei n Scheiben der Aufwand exponentiell steigt und die kleinstmögliche Anzahl von Zügen 2n - 1 beträgt. Bei vier Scheiben sind dies demnach 15 Züge, bei zehn Scheiben bereits 1024, etc.
Spielbare 3D-Simulation mit Graphing Calculator 3D
Die Graphing Calculator 3D-Datei Towers of Hanoi 4 discs Game.gc3 (s.u.) ist eine spielbare Simulation der Türme von Hanoi. Die 3D-Darstellung besteht aus folgenden Komponenten, die mit parametrischen Funktionen erzeugt werden:
- Bodenplatte (entsprechend gestreckter Würfel mit abgerundeten Ecken)
- 3 Stäbe (Zylinder)
- Lochscheiben, bestehend aus zylindrischem Mantel, Kreisfläche mit Loch, Zylinder für Bohrungsinnenseite.
Die Position P und Höhe H jeder Scheibe lässt sich mit Schiebereglern einstellen. Falls eine größere Scheibe über eine kleinere bewegt wird, erscheint ein roter Warnbalken:
Das Ganze ist zugegebenermaßen etwas "hakelig", und es wird auch nicht geprüft, ob eine Scheibe "in der Luft hängt". Um so etwas mit vertretbarem Aufwand umzusetzen, wären Datenstrukturen, wie z.B. indizierbare Felder (arrays) oder Stapel (stacks) erforderlich, die Graphing Calculator 3D auf Grund seiner Konzeption als 3D-Grafiksoftware nicht bietet.
Simulation eines optimalen Spielverlaufs mit Graphing Calculator 3D
Ziel ist es, eine Animation mit einem optimalen Spielverlauf mit Graphing Calculator 3D zu realisieren.
Im Informatikstudium werden die Türme von Hanoi gern als Beispiel herangezogen, um verschiedene Algorithmen (iterativ, rekursiv) zur Lösung des Problems programmtechnisch umzusetzen. Die algorithmische Lösung ist mit Graphing Calculator 3D nicht möglich, vielmehr müssen die Spielzüge vorgegeben werden.
Jedoch kann man durch Definition entsprechender Funktionen für die Darstellung einer Scheibe und für ihre Position / Höhe in Abhängigkeit des Spielzugs das Graphing Calculator 3D-Programm übersichtlich und strukturiert gestalten, so dass der Programmier- / Editieraufwand klein bleibt.
Dabei besteht ein Spielzug aus den drei Teilschritten Scheibe hoch nehmen, über Zielstab positionieren und auf Zielstab ablegen. Bei drei Scheiben ergeben sich somit 21 Teilschritte, bei vier Scheiben 45 Teilschritte.
Eine Variable T dient als Schrittzähler und wird per Animation von 0 (Spielstart) solange inkrementiert, bis sich der Scheibenstapel vollständig auf dem Stab C befindet.
Dies ist in den folgenden Videos zu sehen, bei denen nach Start der Animation der Plotbereich
von
Graphing Calculator 3D live mitgeschnitten wurde (s. 3D Mathe/Tools).
Abschließend sei hier noch ein Bild mit einem größeren Scheibenstapel gezeigt. Die Scheiben wurden mit einem entsprechend skaliertem Super-Ellipsoid und niedriger Auflösung erzeugt. Zwar haben sie kein Loch, jedoch wirken sie im Gegensatz zu den bisher verwendeten "exakten" Scheiben sehr "organisch" - ähnlich wie lackierte Holzscheiben.

