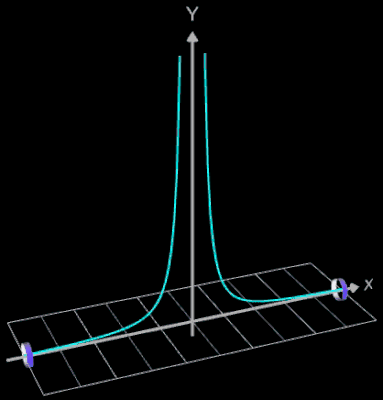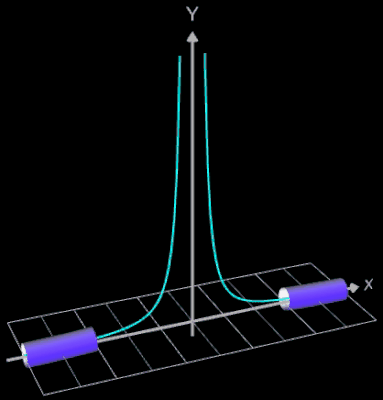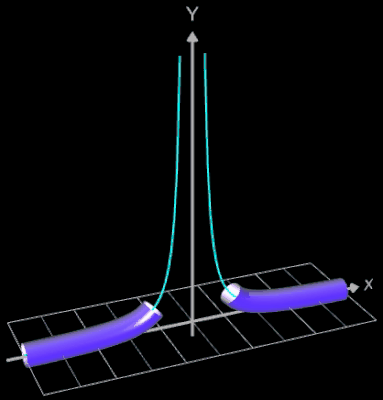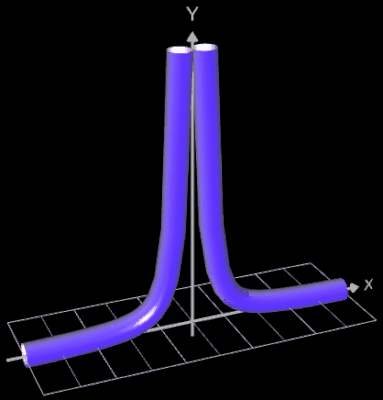
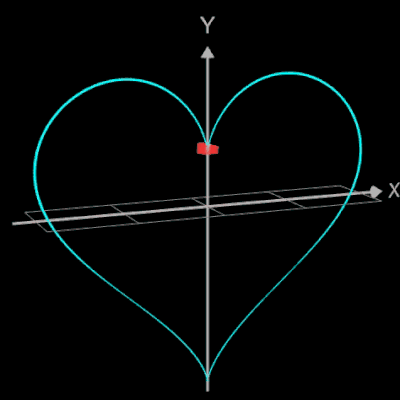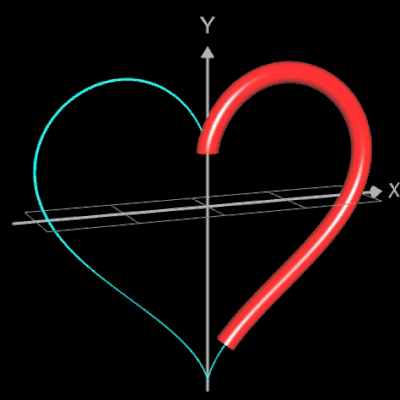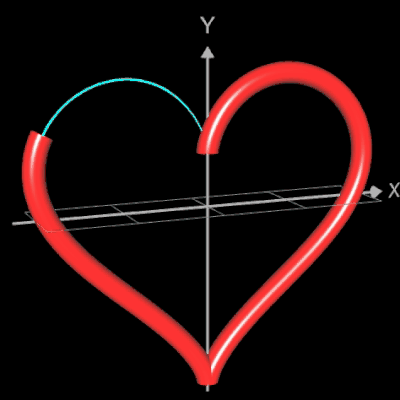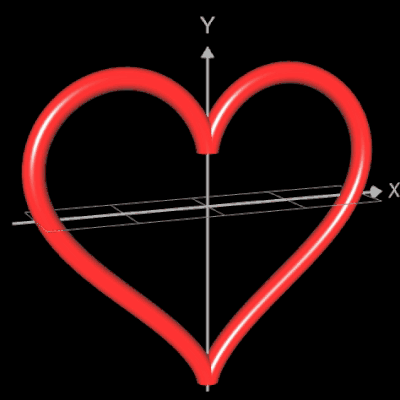
Funktionsgraph als Rohr / Röhre
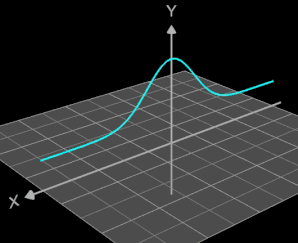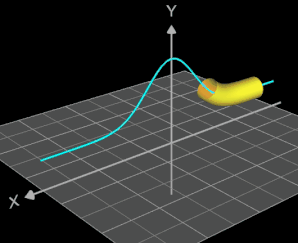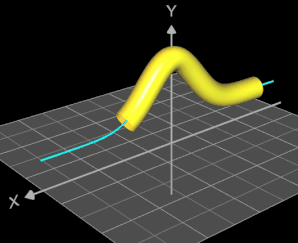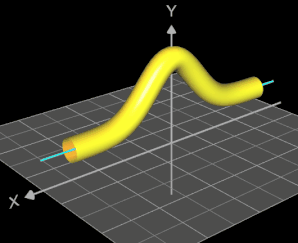
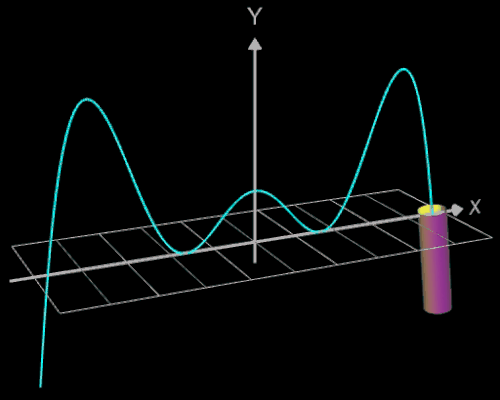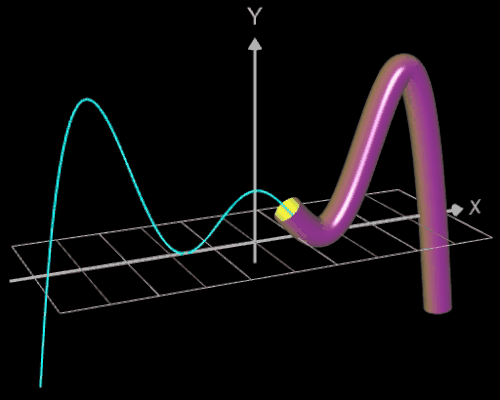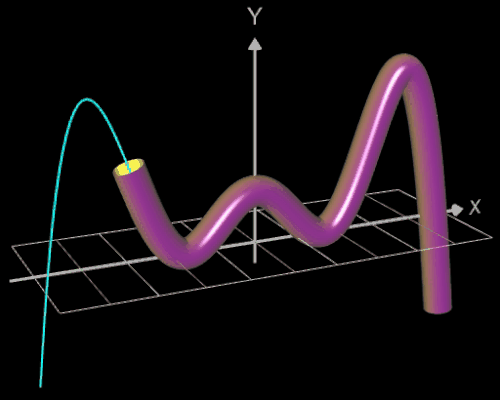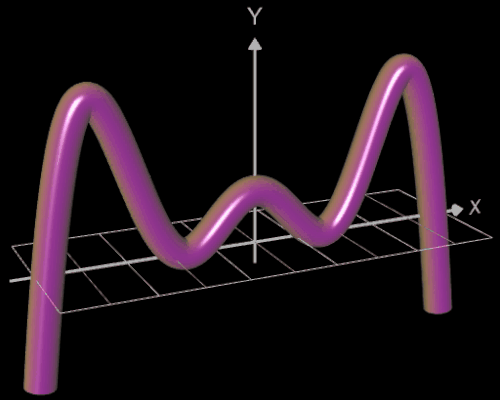
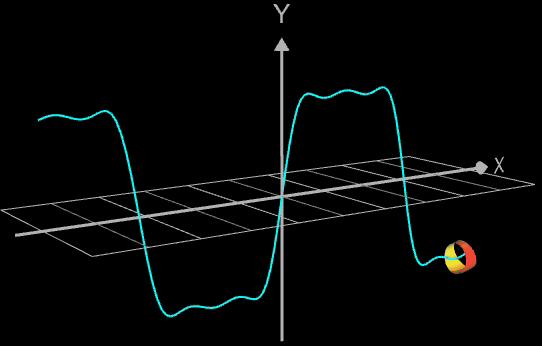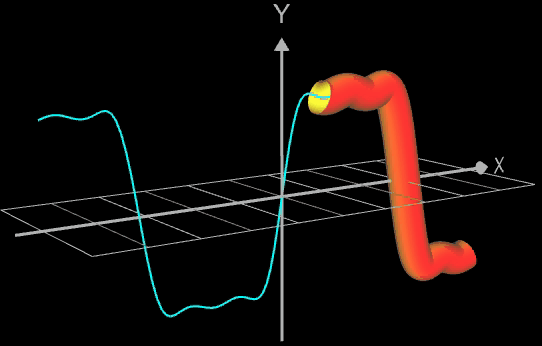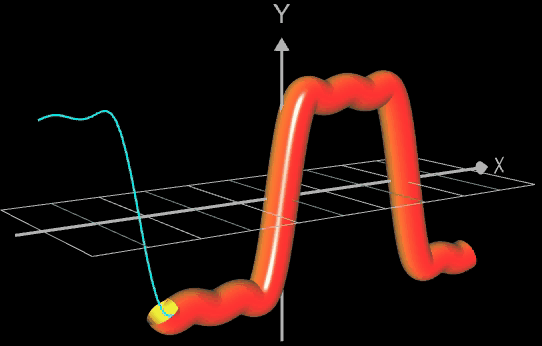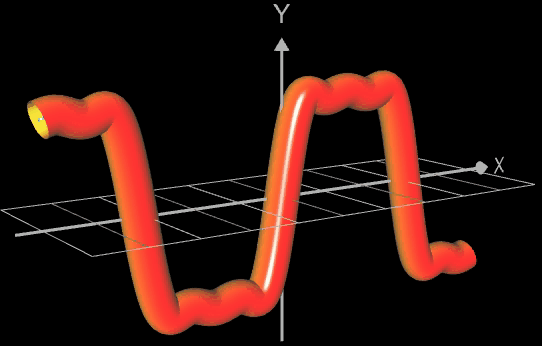
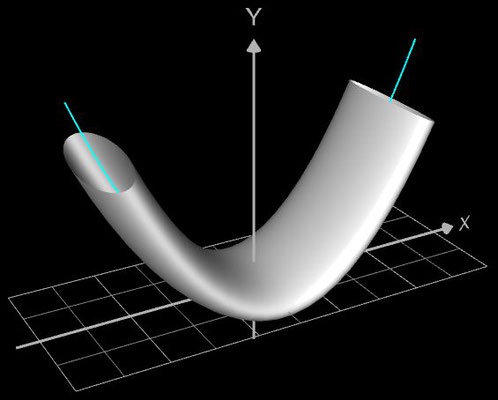
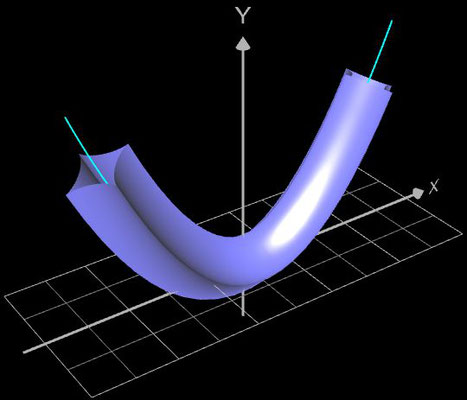
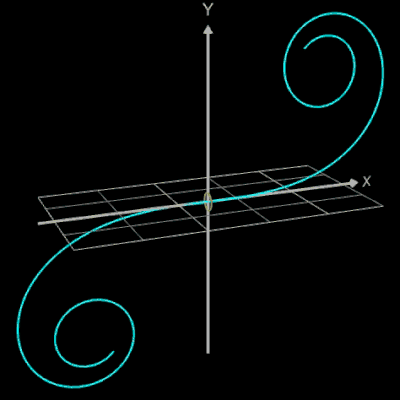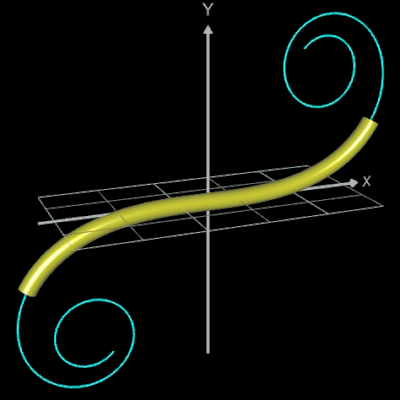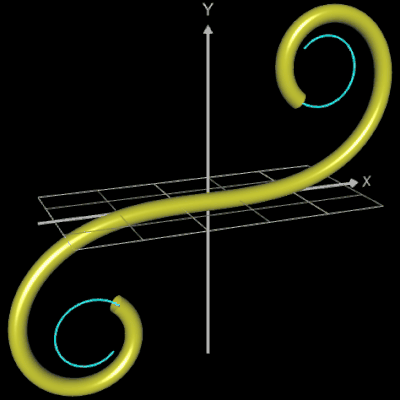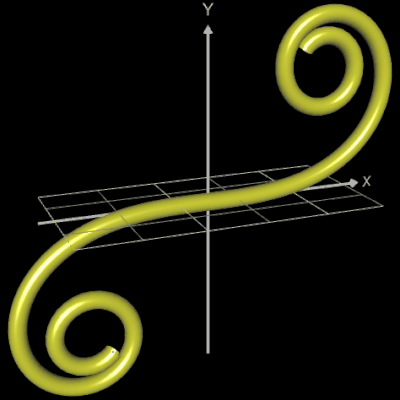
Für eine Simulation zur Thematik Trassierung soll der Graph einer zweidimensionalen Funktion y = f (x) als ein Rohr/Röhre dargestellt werden, d.h. ein "flexibler Zylinder" umschließt den mittig verlaufenden Graph (ähnlich einem Draht mit Kunststoffummantelung) wie es die Animation rechts zeigt.
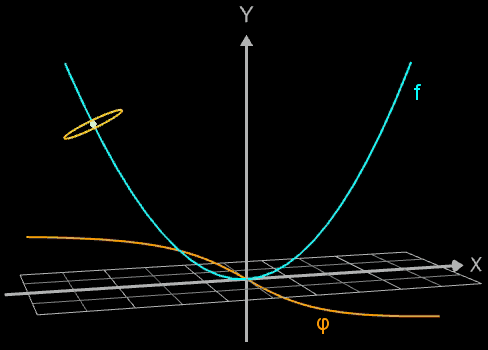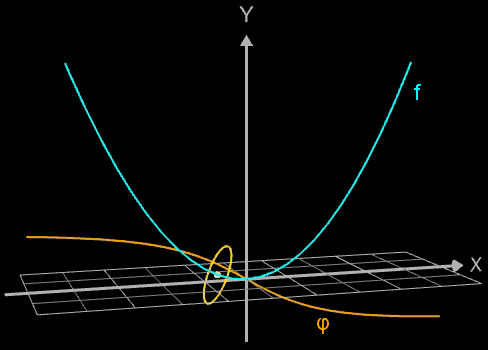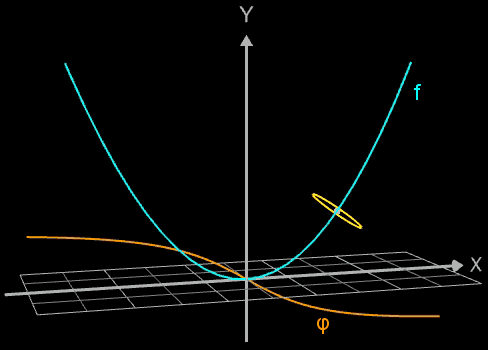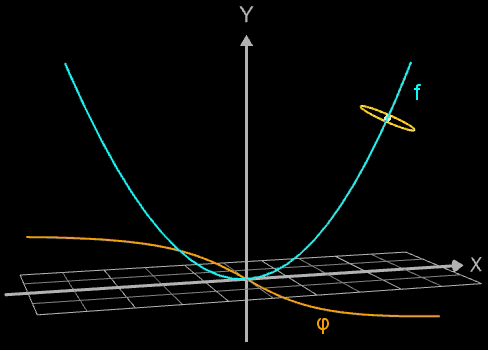
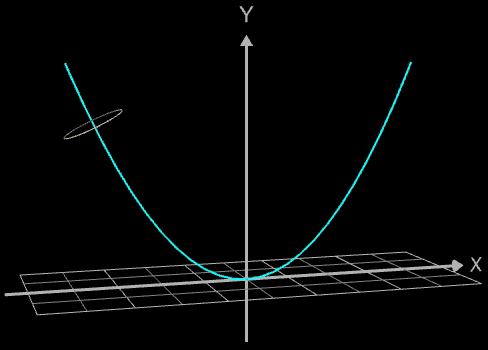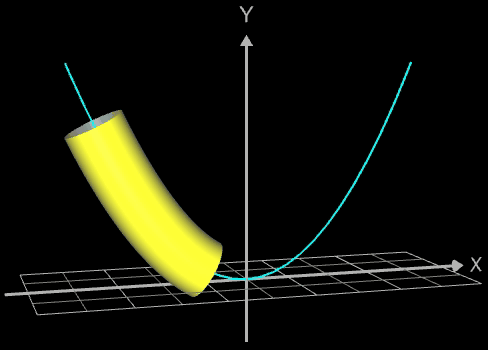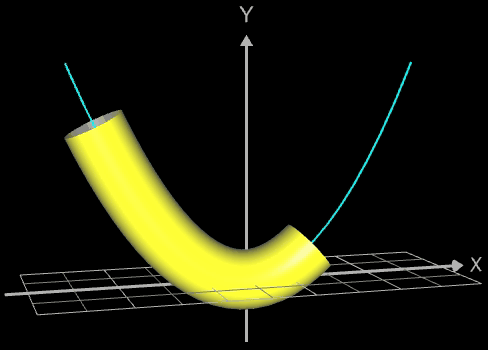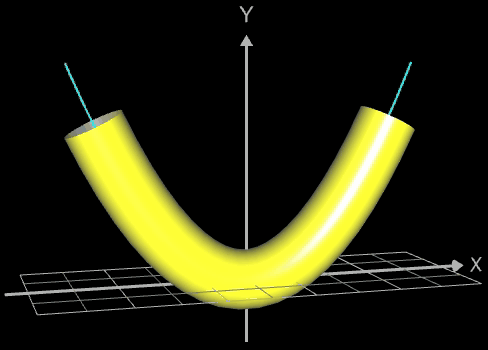
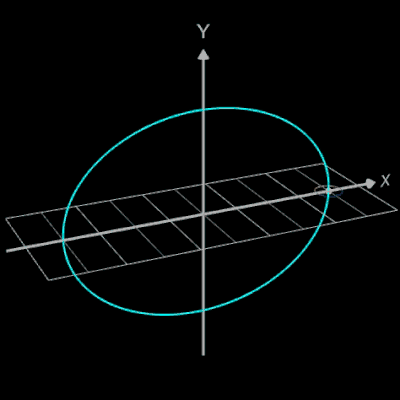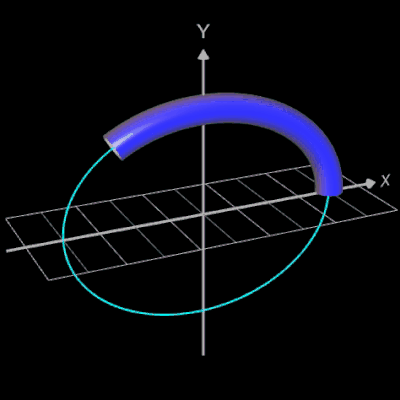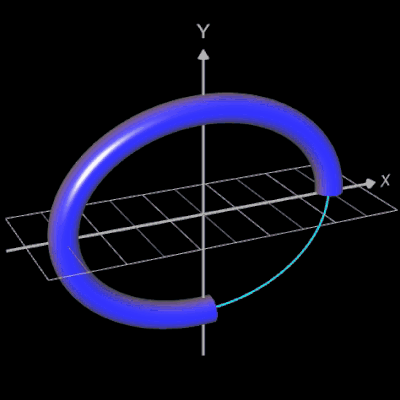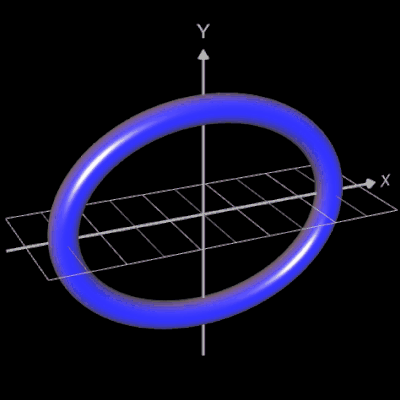
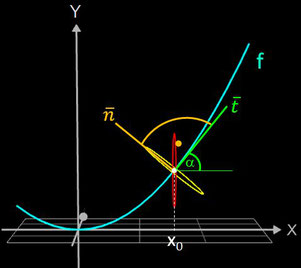
Die Idee zur Lösung ist, an einer Stelle x0 einen Kreis mit dem Radius r (dieser entspricht dem Querschnitt des Rohrs/Röhre) zu erzeugen, dessen Mittelpunkt M auf dem Funktionsgraphen lin (x0 | f (x0)) liegt und dessen Fläche senkrecht auf der Tangente an der Stelle x0 steht (s. folgende Grafik). Die Stelle x0 wird dann durch den Parameter u ersetzt, der die x-Werte im gewünschten Bereich überstreift und so den Mantel des Rohrs/Röhre erzeugt.
Der in nebenstehender Grafik sich an der Stelle
x0 befindende Kreisring q (Querschnitt q des Rohrs) wird per parametrischer Funktion
erzeugt mit
v = 0, ..., 2π:
Für die Tangente t und ihren Steigungswinkel α im Kreismittelpunkt M (x0 | f (x0)) gilt:
- Steigung: f ' (x0) = tan (α)
Der Kreisring ist nun um die durch M in z-Richtung verlaufende Rotationsachse z' zu rotieren, so dass die in M senkrecht zur Tangente stehende Normale n in der Kreisebene liegt.
Der Rotationswinkel φ (x0) beträgt somit φ (x0) = - atan (f ' (x0)). Mit der Rotation um diesen Winkel ergibt sich der korrekte Kreisring (gelb in Grafik) an der Stelle x0 gemäß (s. auch 3D Rotationen um Koordinatenachsen):
Die folgende linke Grafik zeigt die entstehenden Kreisringe beim Überstreichen des Funktionsgraphs. In der rechten Grafik ist schließlich das entstehende Rohr abgebildet, wenn x0 durch a+u(b-a) mit u = 0, ..., 1 ersetzt wird und somit alle x-Werte aus dem Intervall [a, b] des darzustellenden Rohrabschnitts durchlaufen werden.
In der folgenden Galerie werden die Graphen der folgenden Funktionen animiert als Rohr/Röhre dargestellt (von links nach rechts):
- f (x) = 0.4 cos(x) • (-x² + 3)
- f (x) = 2 sin (cos (2x))
- f (x) = 1 / x²
- f (x) = [ exp(a•(x-b)) + exp(a•(b-x)) ] / (2a) + c (Kettenlinie A und B, Parameter s. unter Kettenlinie)
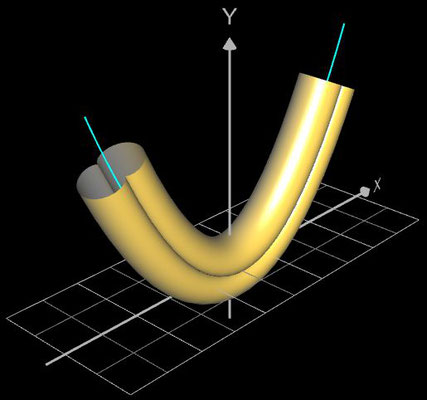
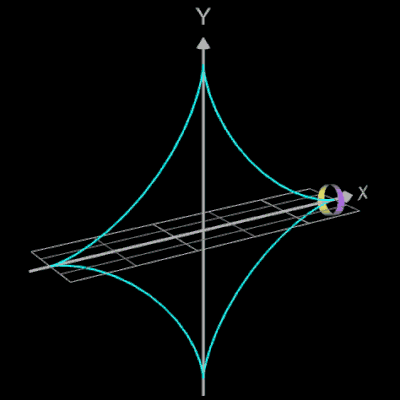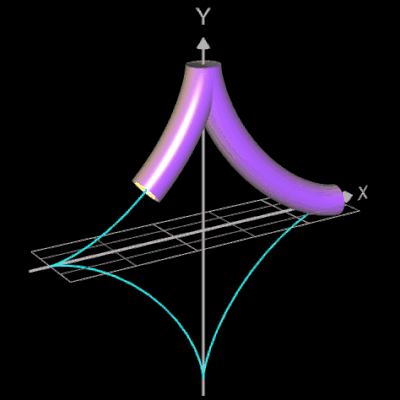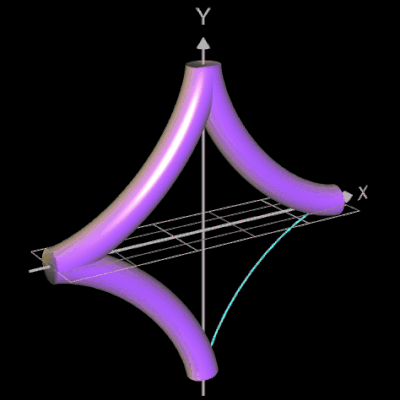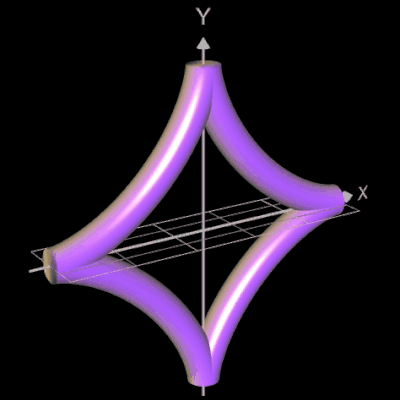
Den Kreis als Querschnittsfunktion q der Ummantelung kann man natürlich auch durch andere parametrische Funktionen ersetzen, wie z.B. durch eine Ellipse, Astroide, Nephroide oder - wie in der Animation unten - durch eine "Zahnradkurve" (s. 3D Zahnrad):
Eine Datei für den Graphing Calculator 3D, mit der sich ein Funktionsgraph als Rohr/Röhre darstellen lässt, finden Sie unten im Download-Bereich.
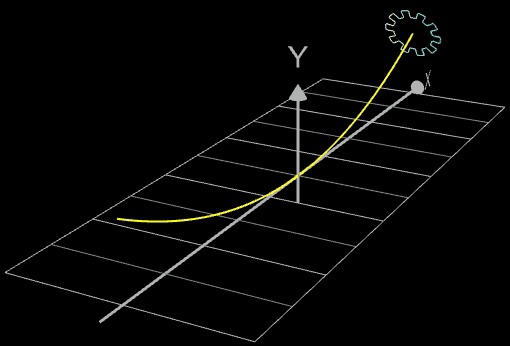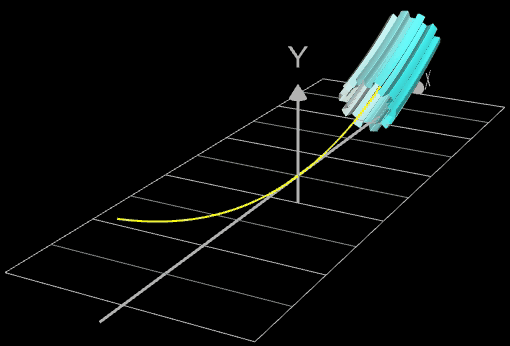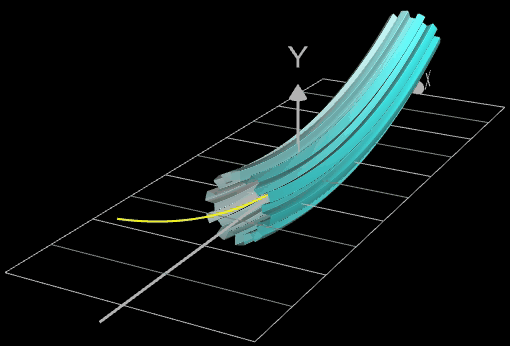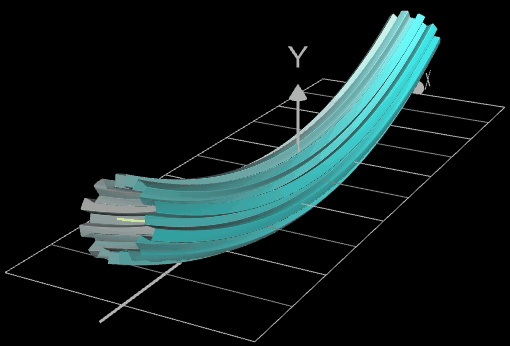
Funktionsgraph als Band
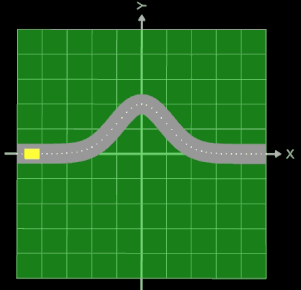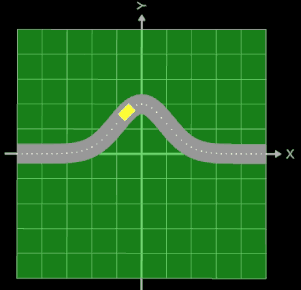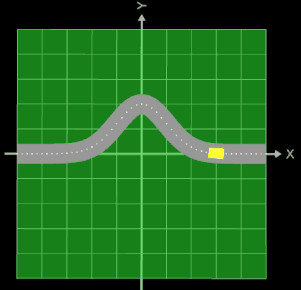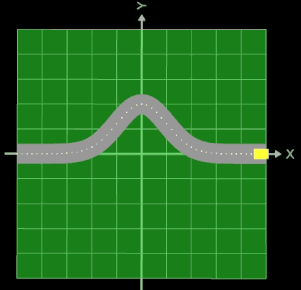
Setzt man in der obigen parametrischen Funktion zur Darstellung des Rohrs/Röhre die z-Komponente zu Null, so ergibt sich ein ebenes Band mit der Breite 2 • r.
Dies kann z.B. beim Thema Trassierung genutzt werden, um einen Straßenverlauf zu modellieren.
In der nebenstehenden Animation stellt der Funktionsgraph von f (Linie aus Punkten) den "Mittelstreifen" der Straße dar, die sich als Band der Breite 2 • r um diesen schmiegt. Das gelbe Rechteck ist ein Fahrzeug, das exakt dem Straßenverlauf f folgt.
Graph einer parametrischen Funktion als Rohr/Röhre
Um den Graph einer parametrischen Funktion y = f (x) mit x = fx (u) , y = fy (u) als Rohr/Röhre darzustellen, liegt es nahe, mein obiges Schema wie folgt zu adaptieren:
- ersetze x0 durch fx (u),
- ersetze f (x0) durch fy (u),
- ersetze die Berechnung des Rotationswinkels
φ (x0)
= - atan ( f ' (x0)
)
der Querschnittsfläche durch
wobei wie oben vorausgesetzt wird, dass die Ableitungen von fx und fy existieren.

Die letzte Ersetzung ist wichtig, denn würde man
φ mit der Funtion atan berechnen
mit
kann
φ für manche Werte
von
x0 zum einen im falschen Quadranten liegen, zum anderen kann der Nenner der Ableitung f ' Null und somit f ' undefiniert sein, wodurch es zu unerwünschten Einschnürungen im
Graph (Rohr/Röhre) kommt. Die
Funktion atan2 [1] liefert hingegen
φ-Werte
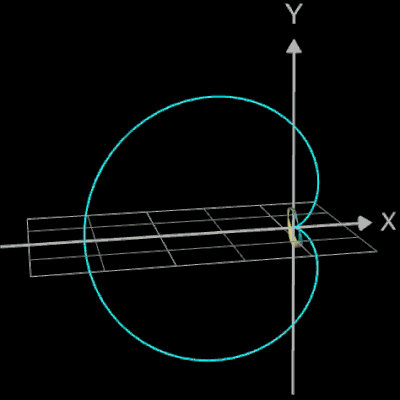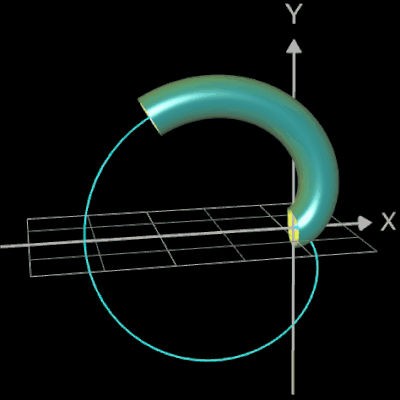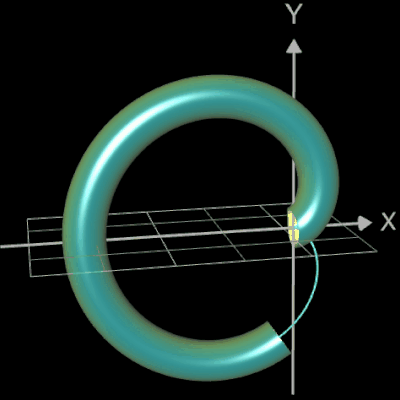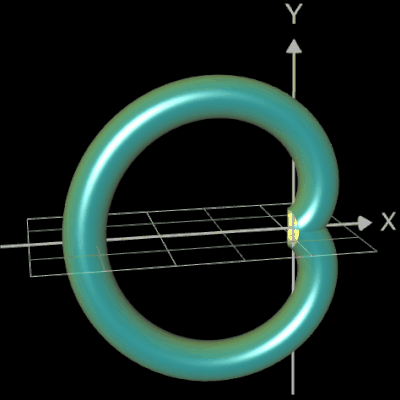
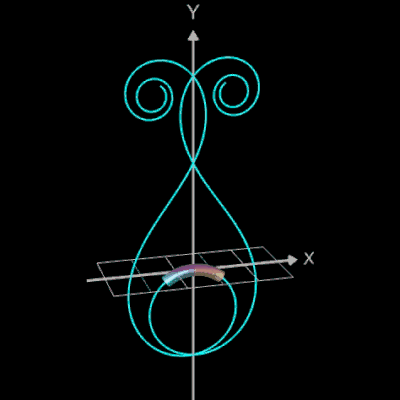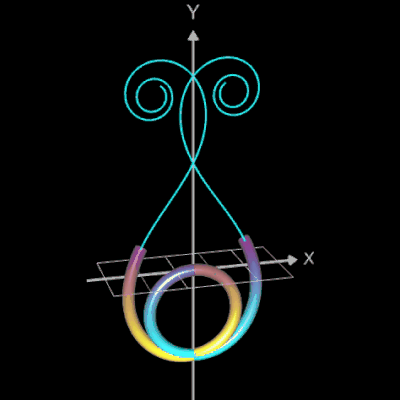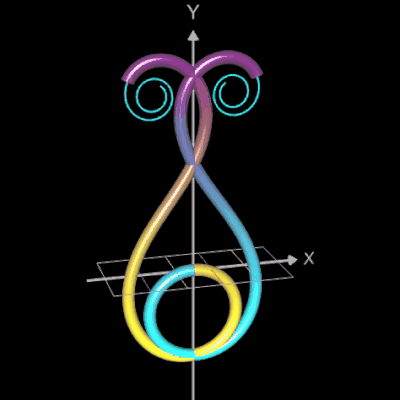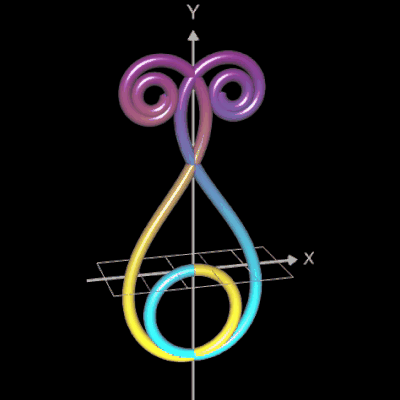
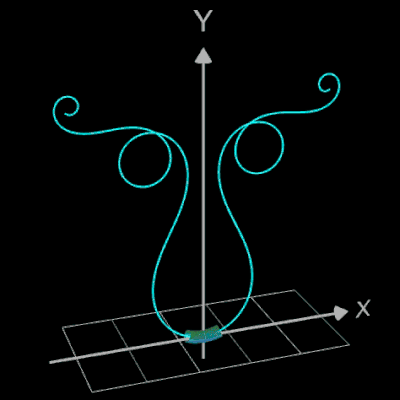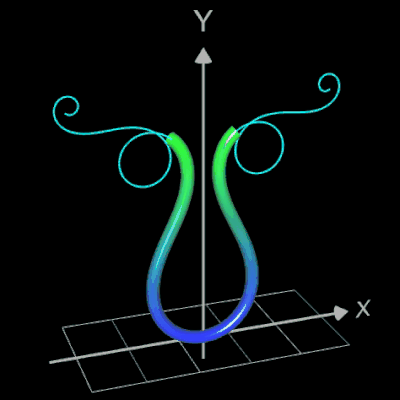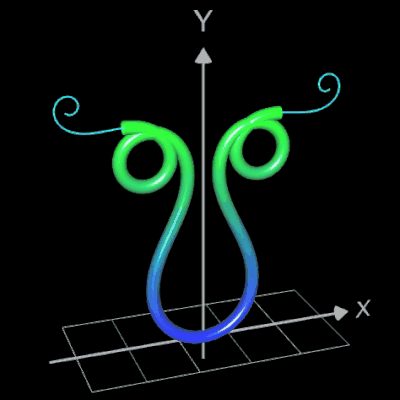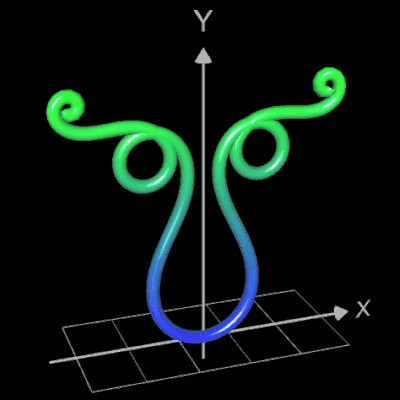
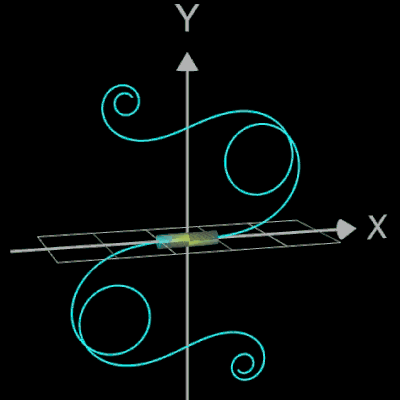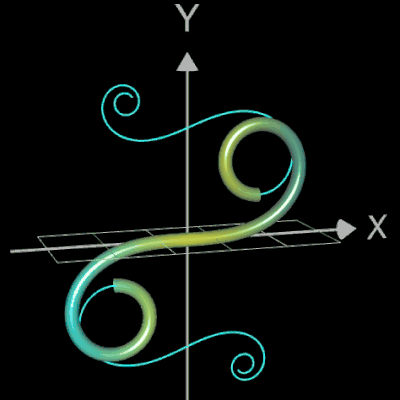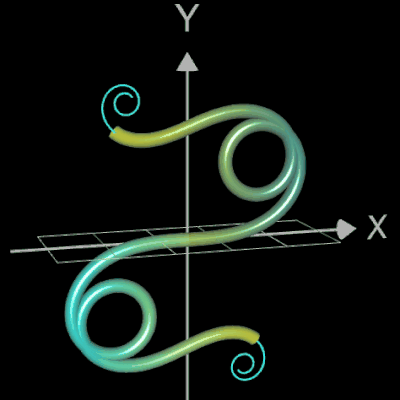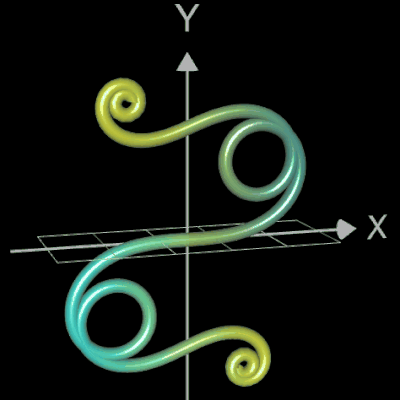
im korrekten Quadranten. Im Bild rechts ist dies am Beispiel einer Klothoide als Rohr dargestellt, die ohne die atan2-Funktion berechnet wurde. Dort kommt es für u-Werte von
(für A = 1) an den entsprechenden Stellen im Graph zu Einschnürungen.
Hier nun einige Beispiele parametrischer Funktionen, deren Graphen in der folgenden Bildergalerie als Rohr/Röhre mit einem kreisförmigen Querschnitt dargestellt sind.
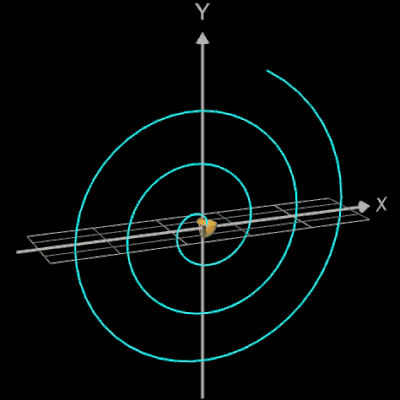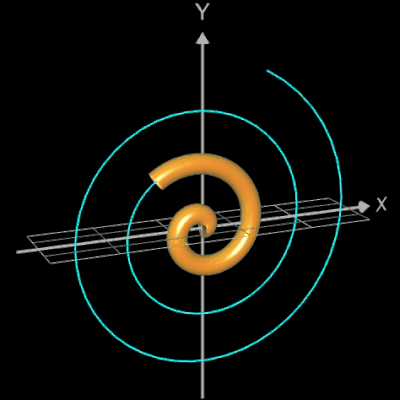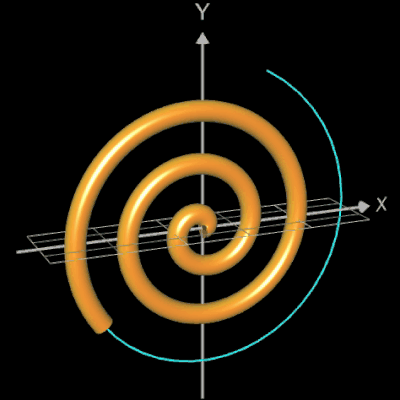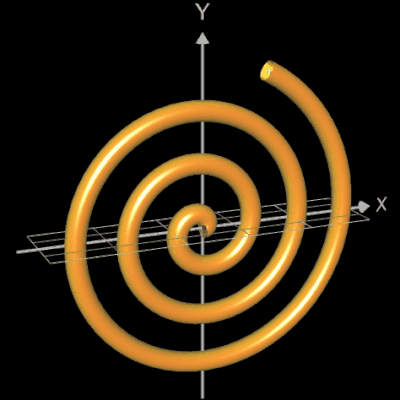
Abschließend sollen noch einige polynomiale Spiralen als Rohr/Röhre dargestellt werden.
Die polynomiale Spirale wird mit der parametrischen Funktion y = f (x) mit x =
fx (t) , y = fy (t) erzeugt, wobei
und p (t) ein Polynom ist. In der folgenden Galerie wurden (von links nach rechts) folgende Größen verwendet:
- p (t) = t3 / 3 - 4 t c = 1 L = 4.3
- p (t) = t5 - 6 t3 + 5.4 t c = 1 L = 2.25
- p (t) = - t4 + 7 t2 c = 0.8 L = 2.7
Weitere Beispiele finden Sie unter Polynomiale Spirale.