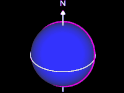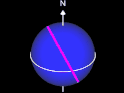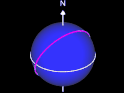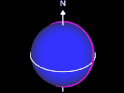
Orthodrome (Großkreis) und Loxodrome

Bei dieser Thematik geht es um die Bestimmung der Distanz zweier Punkte auf einer Kugel – hier am Beispiel der Erde. Diese Problemstellung ergibt sich z.B. bei Flügen oder Schiffstouren, bei denen man von einem Startpunkt S zu einem Zielpunkt Z gelangen will. Ein weiteres Problem dabei ist die Bestimmung des einzuschlagenden Kurses.

Der kürzeste Weg liegt auf einer Orthodrome (Großkreis), jedoch ist dabei eine kontinuierliche Kursanpassung erforderlich.

Dies ist bei einer Loxodrome nicht erforderlich, jedoch ist der Weg auf dieser (deutlich) länger.

Auf den Seiten Orthodrome und Loxodrome wird dies näher untersucht und eine Lösung für die Berechnung und Darstellung hergeleitet.

Die Orthodrome wird auch näher betrachtet auf den Astronomischen Seiten der Universität Utrecht https://www.aa.quae.nl/en/reken/grootcirkel.html, für die ich in 2006 Beispiele, EXCEL-Dateien und Grafiken erarbeitet habe.

Inzwischen gibt es im Internet unzählige Beiträge, Software und Kursrechner zur Thematik. Ich zeige diese dennoch auf meiner Webseite, da die Betrachtungen/Berechnungen ja weiterhin Gültigkeit haben ...