Kursbeispiele
Für die Berechnung und Darstellung einer Orthodrome und Loxodrome zwischen einem Startpunkt S (φs | λs) und einem Zielpunkt Z (φz | λz) auf der Erde habe ich EXCEL gewählt. Die Koordinaten von S und Z werden manuell per Regler eingestellt; alternativ können S und Z aus einer Liste von 910 Orten/Flughäfen weltweit durch Anklicken ausgewählt werden. Die folgende Grafik zeigt die Orte der Liste.
Folgende Größen werden berechnet:
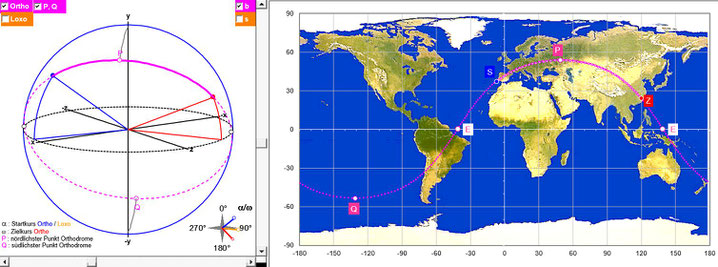
- α : Startkurs der Orthodrome
- ω : Zielkurs der Orthodrome
- α : Kurs der Loxodrome
- g : Weglänge auf Orthodrome
- s : Weglänge auf Loxodrome
- P: nördlichster Punkt der Orthodrome
- Q: südlichster Punkt der Orthodrome
- E: Schnittpunkt von Orthodrome und Äquator
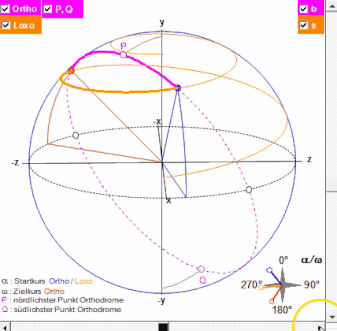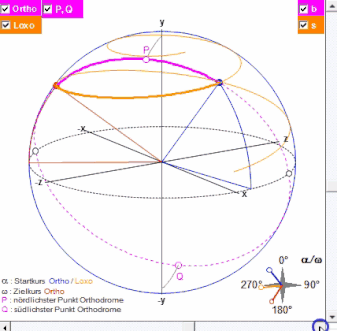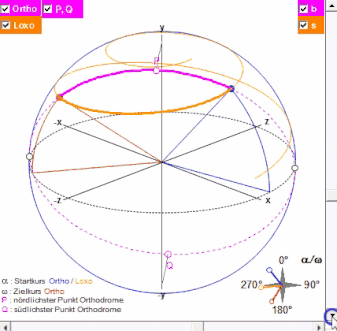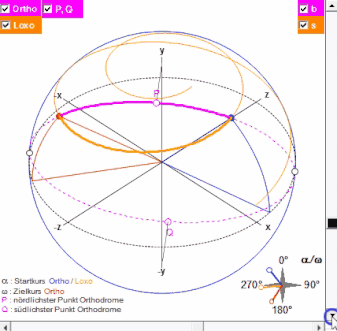
Die Erde und obige Größen werden in einem "3D"-Diagramm dargestellt; die Erde kann mit Hilfe zweier Schieberegler gedreht werden, um die Kursverläufe besser betrachten zu können (s. Animation in folgender Grafik).
Zusätzlich lassen sich noch die Breitenkreise und Meridiane von S und Z einblenden.
Weiterhin werden die berechneten Größen auch auf einer Weltkarte dargestellt, um sich das Szenario besser vorstllen zu können. Bei der Karte handelt es sich um eine äquidistante Zylinderprojektion der Erde, d.h. alle Breitenkreise haben den gleichen Abstand. Durch diese Projektion erscheint die Orthodrome dann als s-förmiger Verlauf, während die Loxodrome für Breiten zwischen 60° N und 60° S nahezu eine Gerade ist. Bei einer Mercatorkarte ist die Loxodrome eine "echte" Gerade (s. unter Loxodrome).
Bei kurzen Strecken ist eine Loxodrome nur unwesentlich länger als eine Orthodrome. Bei hoher Breite und Entfernungen unterhalb von 30
Längengraden liegt der relative Längenunterschied bei weniger als 1 %. Danach steigt er deutlich an.
Im Folgenden nun einige Beispiele ...
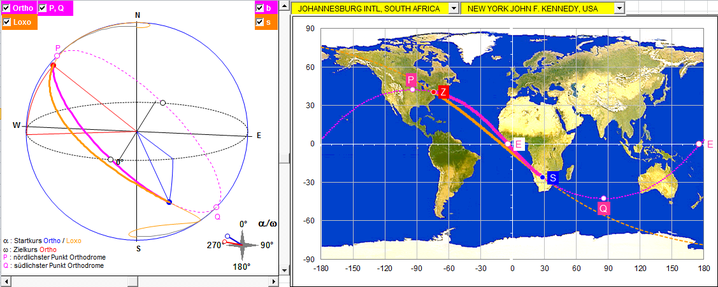
Johannesburg (Südafrika) ► New York JFK (USA)
Der Weg auf der Loxodrome ist nur ca. 100 km länger als der auf der Orthodrome. Start- und Zielkurs der Orthodrome sowie der Kurs der Loxodrome liegen im gleichen Bereich.
Tokyo (Japan) ► Rio de Janeiro (Brasilien)
Während der Weg auf der Orthodrome über den arktischen Bereich der nördlichen Halbkugel mit einer kürzesten Entfernung von ca. 1.100 km zum Nordpol verläuft, wird bei der Loxodrome ein östlicher Kurs eingeschlagen; dieser ist ca. 1.200 km länger.
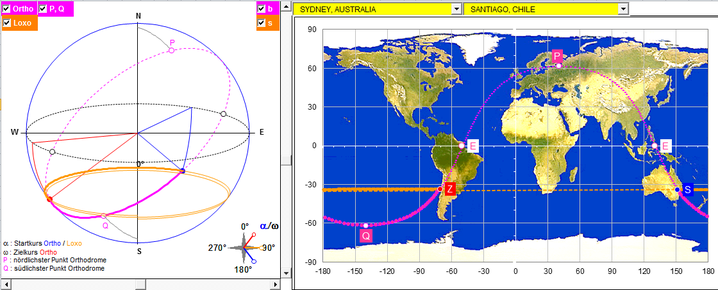
Sidney (Australien) ► Santiago (Chile)
Da die Breiten beider Orte fast die gleichen Werte aufweisen, ist der Abstand der Windungen der Loxodrome recht klein (bei exakt gleichen Breiten sind Loxodrome und Breitenkreis kongruent, vgl. Loxodrome).
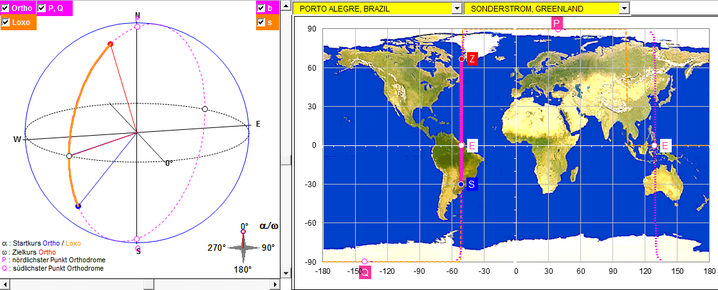
Porto Alegre (Brasilien) ► Sonderstrom (Grönland)
Hier sind die Längen beider Orte nahezu identisch; die Loxodrome entspricht fast dem Meridian.
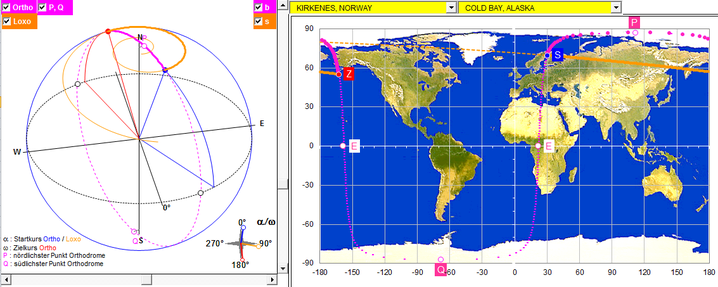
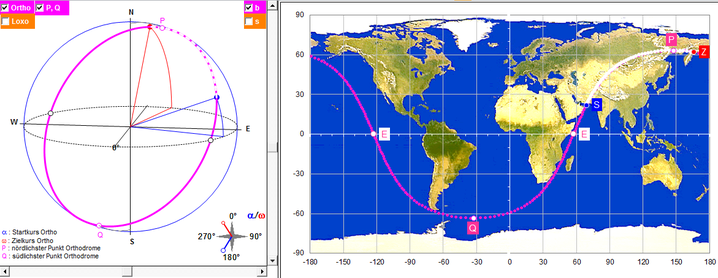
Kirkenes (Norwegen) ► Cold Bay (Alaska)
Längster Seeweg auf einer Orthodrome
Eine interessante Frage ist auch, wie lang der längste Seeweg auf einer Orthodrome ist.
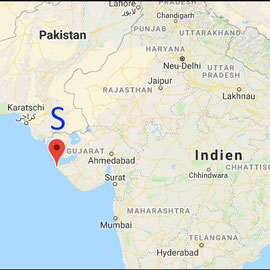
Mit einem Globus aus Kindertagen und durch Ausprobieren mit Hilfe der zugegebenermaßen recht groben Weltkarte in meinem EXCEL-Blatt habe ich folgende Daten bestimmen können:
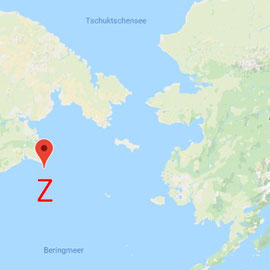
Die Route startet im Arabischen Meer nahe der westlichen Grenze zwischen Pakistan und Indien, verläuft zwischen Afrika und Madagaskar, vorbei an den Südspitzen Afrikas sowie Südamerikas und endet am östlichen Zipfel der russischen Halbinsel Kamtschatka in der Beringsee.
Quelle: https://www.google.com/maps
Die obigen Betrachtungen sind allerdings rein theoretischer Natur, denn zum einen ist bei meiner verwendeten Karte nicht sicher zu erkennen, ob nicht doch eine kleine Insel "im Weg liegt" oder ob sich durch (minimale) Verschiebungen des Start- und Zielpunktes eventuell noch ein längerer Weg ergibt.
Tatsächlich ist der gefundene Seeweg der längstmögliche auf einer Orthodrome. Dies haben zwei Forscher in 2018 mittels einer eigenen Optimierungs-Software herausgefunden [1], [2]. Mit 32.089,7 km ist der optimierte Weg sogar noch ca. 275 km länger als mein berechneter Wert.
Längster Landweg auf einer Orthodrome
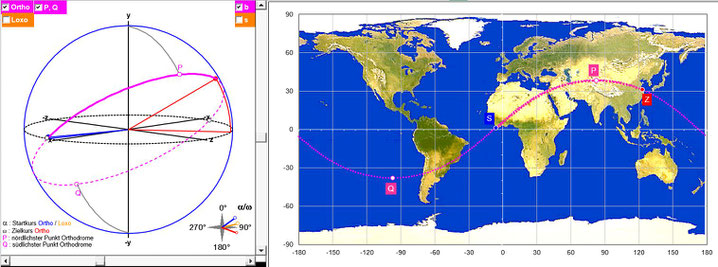
Ebenso kann man die Frage stellen, wie lang der längste Landweg auf einer Orthodrome ist. Da Afrika, Europa und Asien zusammenhängen, liegt es auf der Hand, einen Kurs auf einer Orthodrome von Westafrika nach Ostchina zu suchen. Durch Ausprobieren in EXCEL ist dieser Kurs, der von Liberia nach China führt und ca. 13 570 km lang ist, recht schnell gefunden:

Das kritische "Nadelöhr" ist hierbei der Bereich zwischen nordöstlichem Ägypten (Kairo) / Israel und dem angrenzenden Mittelmeer und Suezkanal. Tatsächlich hat sich inzwischen herausgestellt, dass dieser Kurs nicht die Bedingung erfüllt, ihn trockenen Fußes und ohne Boot zu absolvieren, denn das Tote Meer liegt im Weg. In [1] haben die Verfasser dies nachgewiesen.
Sie geben stattdessen einen Kurs als längstmöglichen an, der von der südlichsten Spitze Portugals bei Sagres nach Jinjiang in Ostchina führt und "nur" ca. 11 241 km lang ist: