Loxodrome
Eine Loxodrome (griech. loxos für "schief" und dromos für "Lauf") ist eine Kurve auf einer Kugeloberfläche (z. B. der Erdoberfläche), die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch "Kursgleiche" genannt wird.
Allgemein gibt es zu jedem Rotationskörper Loxodromen als Kurven konstanten Kurses. So sind beim Zylinder die Loxodromen Schraubenlinien, beim Kegel sind es konische Spiralen (s. auch Helico-Spirale bei Meeresschnecken & Muscheln/3D Modell B.Frassek).
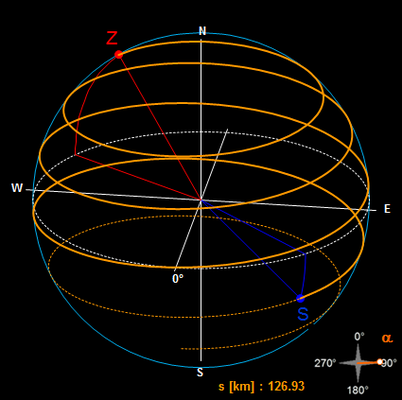
Bei der Kugel windet sich die Loxodrome um diese spiralförmig in Richtung der Pole, erreicht diese im mathematischen Sinn jedoch nie, sondern nähert sich asymptotisch und windet sich dabei unendlich oft um diese. Außer in den beiden Spezialfällen (Schnittwinkel 0° und 90° mit den Meridianen, s.u.) sind Loxodromen nicht geschlossen.
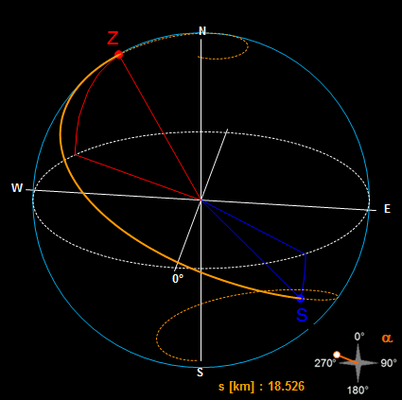
Für zwei Punkte S und Z auf einer Kugel gibt es, ausgehend von S, unendlich viele rechts- sowie linksdrehende Loxodromen von S nach Z. Die folgende Grafik zeigt dies am Beispiel der Erde für je drei Loxodromen mit westlichem bzw. östlichem Kurs.
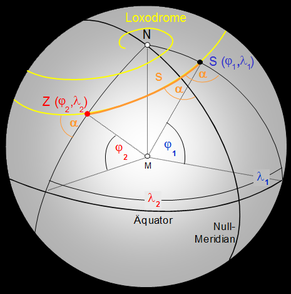
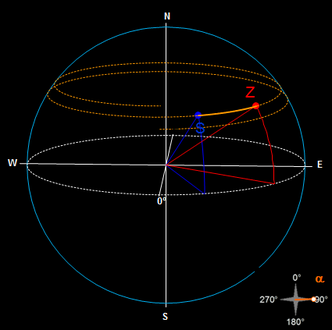
Im Folgenden soll für zwei Orte S (φS|λS) und Z (φZ|λZ) auf der Erde der Weg s auf der kürzesten Loxodrome und der erforderliche Kurswinkel α bestimmt werden.
Bis auf die erwähnten Spezialfälle (s.u.) ist die Wegstrecke auf der Loxodrome stets länger als der Weg auf der Orthodrome.
Für die Loxodrome gilt [1]:
Für die grafische Darstellung der Loxodrome durch die Punkte S und Z wird S festgehalten, λ wird variiert und φ errechnet gemäß
Berechnung von Kurswinkel α und Weg s auf der Loxodrome
Für den Kurswinkel α der Loxodrome ergibt sich gemäß obiger erster Gleichung:
und für den Weg s schließlich
Dieser Winkel muss noch entsprechend in der Berechnung berücksichtigt werden: zum einen hinsichtlich der nautischen Winkelkonventionen (s. Grundlagen), zum anderen für die kürzere der beiden möglichen Loxodromen (s. folgende Grafik).
Spezialfälle der Loxodrome
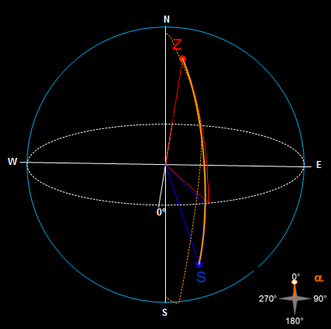
Fall λS = λZ
Falls Start- und Zielpunkt annähernd die gleiche Länge aufweisen, so nähert sich der Bogen s auf der Loxodrome dem Meridian, der Schnittwinkel somit dem Wert 0° und die Länge von s der des Bogens b auf der Orthodrome. Beim folgenden Beispiel beträgt die Längendifferenz 2°.
Im Grenzfall der gleichen Länge, d.h. Loxodrome und Meridian sind kongruent, sind die obigen Gleichungen für s und α nicht definiert; die Berechnung beider Größen erfolgt dann mit den entsprechenden Gleichungen der Orthodrome.
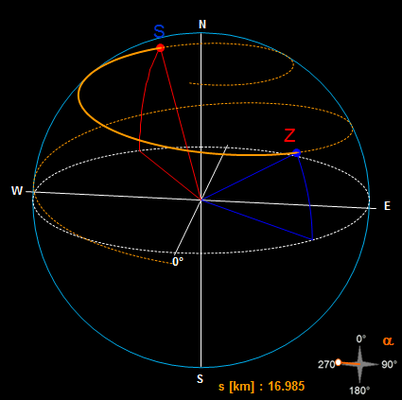
Fall φS = φZ
Falls Start- und Zielpunkt annähernd die gleiche Breite aufweisen, so nähert sich der Bogen s auf der Loxodrome dem Breitenkreis, der Schnittwinkel der Loxodrome mit den Meridianen dem Wert 90° und die Länge von s der des Bogens b auf der Orthodrome. Die Breitendifferenz im folgenden Beispiel beträgt 0.5°.
Im Grenzfall der gleichen Breite, d.h. Loxodrome und Breitenkreis sind kongruent, sind die obigen Gleichungen für s und α nicht definiert; die Berechnung beider Größen erfolgt dann mit den entsprechenden Gleichungen der Orthodrome.
Kartendarstellung der Loxodrome
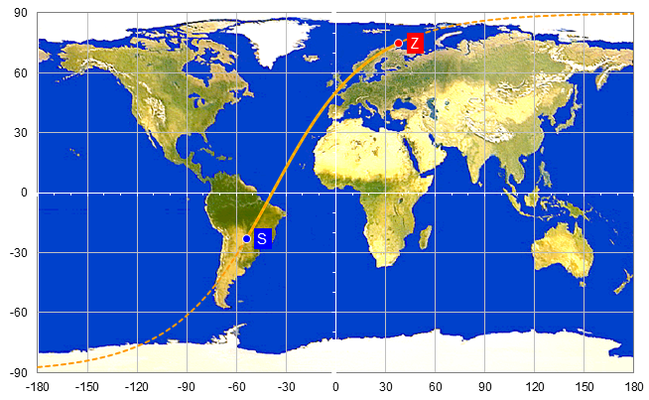
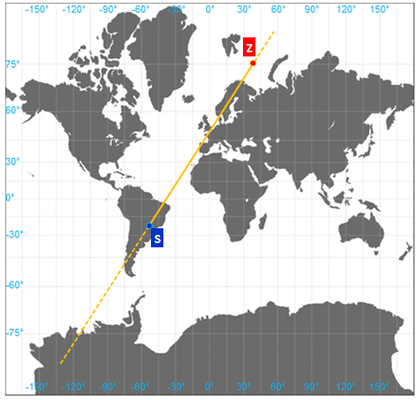
Auf einer Karte mit äquidistanten Breitenkreisen erscheint die Loxodrome als gebogene (s-förmige) Linie, wie das Beispiel in der folgenden linken Abbildung zeigt. Auf einer winkeltreuen Mercator-Karte ist die Loxodrome hingegen eine Gerade (s. folgende rechte Grafik).
Für die Darstellung auf einer Mercator-Karte wird ein Punkt (φ | λ) der Loxodrome umgerechnet in einen Kartenpunkt (x | y) gemäß
wobei λ0 die Länge des Kartenmittelpunktes ist [2].
Kursbeispiele für die Loxodrome
Kursbeispiele mit verschiedenen Kombinationen von Startpunkt S und Zielpunkt Z sowie dem alternativen Weg auf der Orthodrome finden Sie unter Kursbeispiele.
Quellenverweise
[1] Gellert, W. et al: Kleine Enzyklopädie Mathematik, Pfalz Verlag Basel, Sphärische Trigonometrie, S. 333