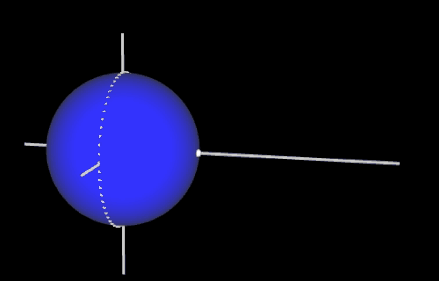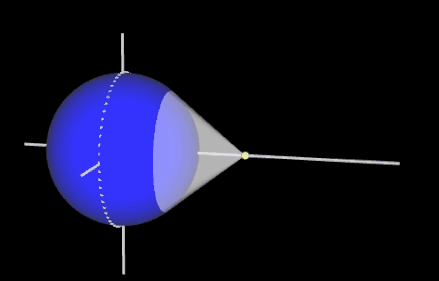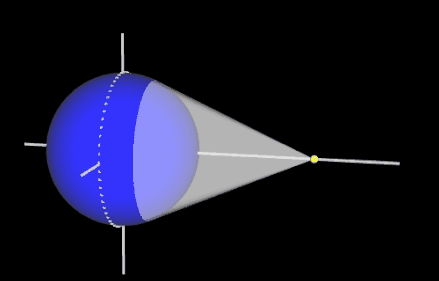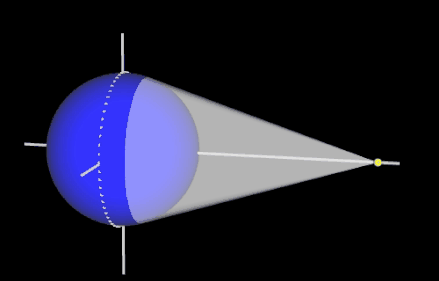
Beleuchteter Teil einer Kugel
Wo verläuft bei einer beleuchteten Kugel die Schattenkante, also die Schnittlinie von Lichtkegel und Kugel?
Dieses kürzlich bei einem Schüler im Rahmen des Gestaltungsunterrichts aufgetretene Problem und meine Lösung hierzu passt ganz gut zum Thema Rotationskörper.
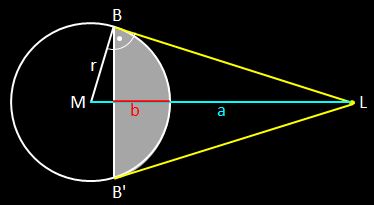
Dazu betrachte man die beiden folgenden Szenarien, die Längsschnitte der Situation zeigen. Die Kugel ist dann ein Kreis mit Radius r und
Mittelpunkt M. Die Lichtquelle L befindet sich im Abstand a (= Strecke LM)
zum Mittelpunkt M und beleuchtet ein Kugelsegment mit der Höhe b.
Die Schattenkante ist der Rand des beleuchteten Kugelsegments und entspricht im Längsschnitt der Geraden BB'. Gesucht ist hier also die Strecke b.
Man erkennt unmittelbar: je weiter die Lichtquelle entfernt ist (gleichbedeutend mit je größer a ist), desto größer ist der beleuchtete Bereich (gleichbedeutend mit desto größer ist b).
Die Strecke BL ist eine Tangente, d.h. der Radius r (= Strecke MB) bildet mit der Strecke BL einen rechten Winkel. Mithin ist das Dreieck MBL ein rechtwinkliges Dreieck mit den Katheten r und BL und der Hypotenuse a (= Strecke ML). Zur Berechnung von b werden weitere Größen eingezeichnet:
Die Höhe h auf der Hypotenuse a teilt von dieser die Strecke p ab. Nach dem Kathetensatz von Euklid gilt:
Für b gilt:
Klammert man r aus der letzten Gleichung aus:
so sieht man den oben erwähnten Zusammenhang, wie sich b mit dem Abstand von a verändert, deutlicher:
- wenn a = r, d.h. die Lichtquelle ist direkt auf der Kugeloberfläche, ergibt sich:
- je größer a wird, desto kleiner wird der Bruch; somit geht der Wert der Klammer gegen 1 und damit nähert sich b dem Radius r.
- Im Grenzfall a = ∞ ist b = r.
Für die Konstellation Erde - Sonne mit einem mittleren Erdradius von r ≈ 6371 km und dem ungefähren Abstand Erde zur Sonne a ≈ 150 000 000 km ergibt sich, dass das beleuchtete Kugelsegment fast der halben Erdkugel entspricht:
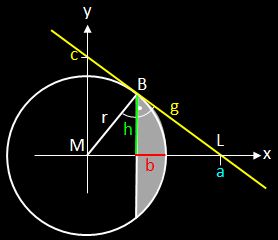
Für die Animation oben auf der Seite wird ohne Beschränkung der Allgemeinheit der Kugelmittelpunkt M in den Ursprung eines Koordinatensystems gelegt:
Der Lichtkegel wird durch Rotation der Geraden g (x) = m x + c um die x-Achse in den Grenzen [r-b, a] erzeugt (s. Rotationskörper-Grundlagen). Die Parameter m und c der Geraden sind noch zu bestimmen:
Nach Pythagoras gilt:
Mit Hilfe des 2. Strahlensatzes ergibt sich:
Die Steigung m der Geraden g ergibt sich per Steigungsdreieck zu: