Gibbs'sches Phänomen
Ein interessanter Effekt - das Gibbs'sche Phänomen (auch "Ringing" genannt) - taucht bei der additiven Synthese von Rechteck-, Puls- und Sägezahnschwingungen auf. Als Beispiel diene hier die Sägezahnfunktion f in der folgenden Abbildung. Diese Funktion ist stückweise linear, reell und periodisch mit einer Periode der Länge 2π.
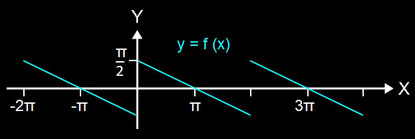
Die folgende Abbildung zeigt eine Teilsumme (s7) der zu f gehörenden Fourier-Reihe
Diese enthält ausschließlich Sinusfunktionen.
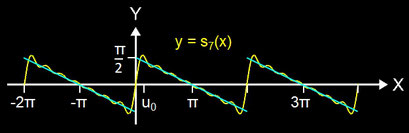
Die Konvergenz der Partialsummen
ist besonders überraschend in der Nähe von Sprungdiskontinuitäten von f. Um die lokalen Extrema von sn zu finden, setzen wir
Für das Intervall ]0, π[ erhalten wir lokale Maxima an den Punkten ui und lokale Minima bei vi :
Für den kleinsten, positiven Wert eines lokalen Maximums von sn, also u0 (hier liegt ein globales Maximum vor), ergibt sich
Dies bedeutet, dass für große n die Teilsummen den erwarteten Wert von π/2 an der Sprungunstetigkeit überschreiten. Dieses Verhalten ist das Gibbs-Phänomen mit dem man allgemein in der Mathematik das typische Verhalten von Fourierreihen in der Umgebung von Sprungsstellen bezeichnet: entwickelt man eine Fourierreihe für eine unstetige Funktion, wie dies der Fall ist für die zuvor genannten Funktionen, so ergeben sich an den Sprungstellen (Unstetigkeitsstellen) typische Über- und Unterschwinger.
Dieser Fehler ist von prinzipieller Art, d.h. er ließe sich auch nicht vermeiden, wenn man unendlich viele Summanden berücksichtigen würde. Durch eine Erhöhung der Anzahl n der Summanden wird zwar der fehlerhafte zeitliche Bereich enger, nicht jedoch die maximale Abweichung der Über- und Unterschwingungen.
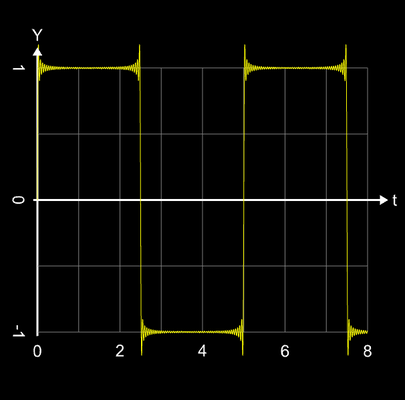
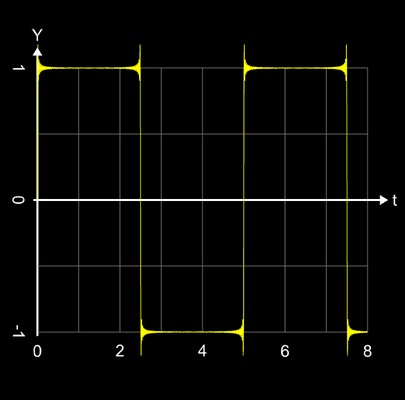
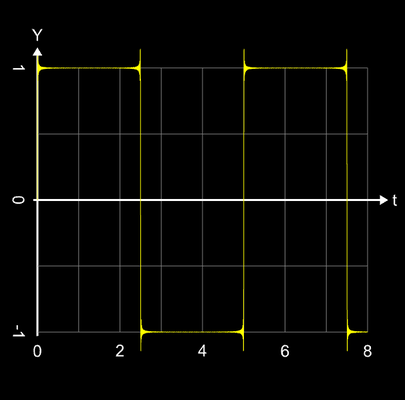
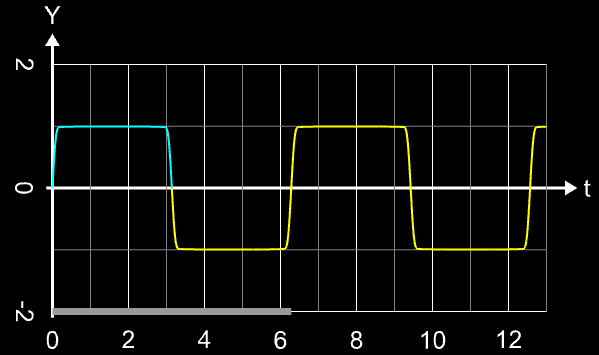
Die folgende Bildsequenz zeigt dies hier am Beispiel einer Rechteckschwingung mit der Amplitude 1 für
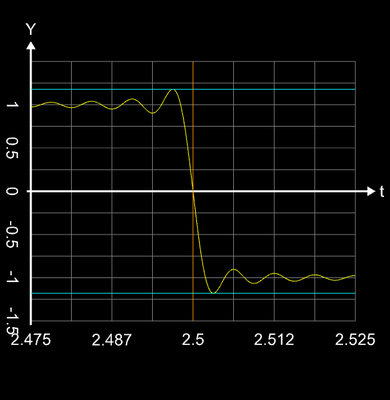
n = 50, n = 100, n = 200 und n = 400 (Bilder bitte zoomen); das letzte Bild ist eine Ausschnittvergrößerung für n = 400 im blau markierten Bereich um die Sprungstelle.
Es lässt sich zeigen, dass für unendlich viele Fourier-Summenglieder die relative Höhe der Unter- bzw. Überschwingung in einer Richtung bezogen auf die halbe Sprunghöhe einem Grenzwert (s. horizontale blaue Linie im letzten Bild oben) entgegenstrebt [1] [2], der sich errechnet zu
Dieser Wert ird auch als Wilbraham–Gibbs-Konstante bezeichnet; er wird numerisch berechnet.
Somit ergibt sich ein prozentualer Fehler von ca. 18 % (17,89797444... %) der Sprunghöhe.
Reduktion des Gibbs'schen Phänomens
Das Gibbs'sche Phänomen mit seinen Unter-/Überschwingungen an den Sprungstellen (Unstetigkeitsstellen) eines Signals lässt sich zu einem Großteil unterdrücken, indem jeder Summand der Fourierreihe mit der Periode T mit Hilfe der normalisierten sinc-Funktion
gewichtet wird:
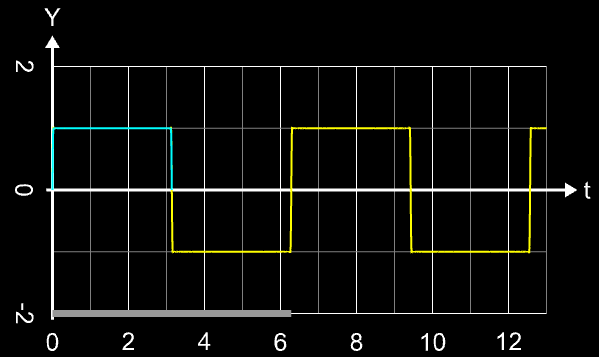
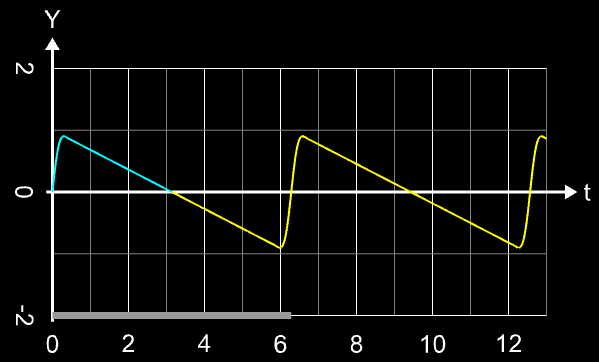
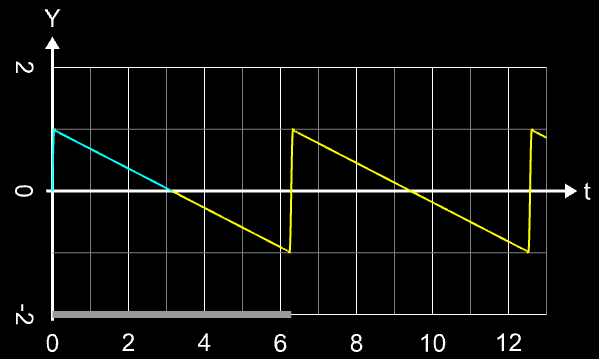
Durch Quadrieren der nsinc-Funktion lässt sich das Gibbs'sche Phänomen fast vollständig unterdrücken, wie die folgende Bildsequenz am Beispiel einer Rechteckschwingung und eines Sägezahns - jeweils mit n = 20 (links) und n = 100 (rechts) zeigt.